Capítulo 7 - Recorte

Siguiendo nuestro modelado en dos dimensiones, hablaremos de una operación importante acerca de líneas y polígonos. El recorte (o clipping, en inglés) modifica las líneas y polígonos a visualizar debidos a una región que los limita. Técnicamente, se trata de una intersección de dos entidades geométricas. Típicamente, la región de recorte es un rectángulo vertical, cuyos lados son paralelos a los ejes del sistema de coordenadas, que suele representar la vista de nuestra escena o la pantalla en sí.

Existen varios algoritmos y métodos para hacer el recorte. Por ahora, sólo miraremos aquellas técnicas analíticas. Esto significa que aplicaremos la operación de recorte a nuestro modelo en nuestro sistema de coordenadas matemático de nuestro mundo y escena. Existen otros métodos de recorte que se pueden aplicar en la etapa de conversión del modelo a píxeles. Trataremos estas técnicas en posteriores capítulos.

Veremos varios métodos para varios casos de recorte, como son el recorte de líneas y polígonos en un rectángulo vertical, al igual que en una región de recorte descrita por un polígono.

Recortando Líneas

Realmente, no pretendemos recortar líneas sino más bien segmentos. Como un segmento se describe por sus puntos extremos, no tenemos que consultar la infinidad de puntos que componen tal segmento.

De la misma manera que analizamos el recorte de puntos individuales, podemos aplicar la misma lógica para los puntos extremos de un segmento. El resultado es cuatro casos diferentes. Si ambos extremos están dentro del rectángulo de recorte, entonces no tenemos que hacer nada más que aceptar el segmento. Si un extremo está dentro y el otro fuera del rectángulo, entonces el segmento cruza uno de los lados de la región de recorte. Tenemos que calcular el punto de intersección lo cual modificará el extremo del segmento externo para que sea interno al rectángulo de recorte. Si ambos extremos están fuera del rectángulo de recorte, entonces el segmento puede estar completamente fuera del rectángulo, por lo que es rechazado inmediatamente. Sin embargo, tal segmento podría cruzar dos lados del rectángulo. En este caso, tenemos que realizar dos cálculos de intersección, modificando ambos extremos del segmento para que éste sea interior al rectángulo de recorte.

Veremos varios algoritmos para solucionar este problema: Algoritmo Exhaustivo, Algoritmo de Cohen-Sutherland, Algoritmo de Cyrus-Beck, Algoritmo de Liang-Barsky, y Algoritmo de Nicholl-Lee-Nicholl.

Recortando Polígonos

Lo normal es que nuestra escena contenga varios polígonos y no segmentos sueltos. Como nuestra vista limita el contenido de la escena que podemos mostrar, tendremos que recortar los polígonos de la escena para eliminarlos de la vista o dibujarlos parcial o completamente. Como representamos los polígonos mediante los segmentos que forman sus aristas, al recortar los polígonos en un rectángulo, acabaremos eliminando, aceptando, o recortando las aristas existentes y posiblemente añadiendo nuevas. Los diferentes resultados dependen del tipo de polígono a recortar.

Un polígono convexo que intersecta un rectángulo dará lugar a un polígono convexo. Un polígono cóncavo recortado por un rectángulo puede resultar en uno o varios polígonos cóncavos o convexos.

Veremos varios algoritmos para recortar polígonos: Algoritmo de Sutherland-Hodgman, Algoritmo de Liang-Barsky, y Algoritmo de Weiler-Atherton.

Recortando Puntos

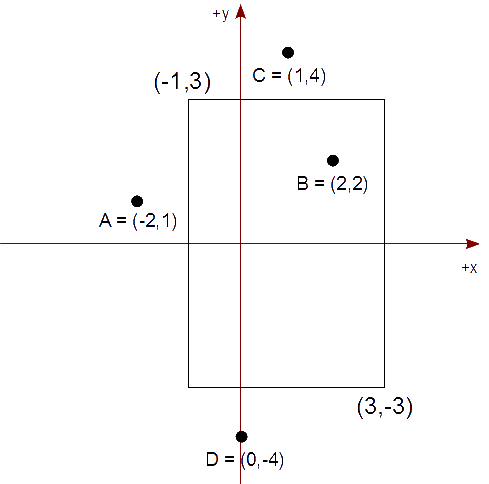
Veamos el problema sencillo de recortar puntos. Para este caso, sólo necesitamos aceptar o rechazar tal punto. Nos basamos en los valores de las coordenadas del punto y de las del rectángulo vertical. Como el rectángulo está de pie, sólo tenemos que considerar las coordenadas de ciertos ejes y tratarlas como condiciones de contorno. Por consiguiente, el punto P = (x,y) debe satisfacer todas las siguientes inecuaciones para aceptarlo como un punto interior al rectángulo:

x_izq ≤ x ≤ x_der
y_inf ≤ y ≤ y_sup

donde, x_izq, x_der, y_inf, e y_sup son las coordenadas que describen los lados del rectángulo vertical de recorte izquierdo, derecho, inferior, y superior, respectivamente. Esto lo podemos ver fácilmente en las figuras 1 y 2:

Algoritmo Exhaustivo

Si no podemos aceptar inmediatamente un segmento, entonces comprobamos tal segmento con cada arista del rectángulo. Cada comprobación da lugar a una intersección con un lado del rectángulo, acortando el segmento hasta que esté dentro de ello. A continuación, comprobamos cada intersección es interior a nuestro rectángulo de recorte.

Con esta solución, debemos resolver varias ecuaciones por cada intersección entre segmento y arista del rectángulo. Podríamos usar la fórmula de la intersección de la pendiente, pero ésta sirve para líneas (infinitas) y no para segmentos. Además, esta fórmula no puede describir líneas verticales. Sin embargo, podemos usar una forma paramétrica para describir cualquier punto del segmento con los extremos (x₀,y₀) y (x₁,y₁):

x = x₀ + t (x₁ - x₀)
y = y₀ + t (y₁ - y₀)

donde, t queda comprendido en el intervalo [0,1].

También debemos describir cada arista del rectángulo de la misma forma con los extremos (x′₀,y′₀) y (x′₁,y′₁):

x′ = x′₀ + t′ (x′₁ - x′₀)
y′ = y′₀ + t′ (y′₁ - y′₀)

donde, t′ queda comprendido en el intervalo [0,1].

Nos interesa el punto de intersección del segmento con cada arista del rectángulo de recorte. Esto significa que debemos encontrar el punto común para ambos segmentos, por lo que (x,y) = (x′,y′). Como sabemos la coordenada de intersección para un arista concreta del rectángulo vertical, el cálculo de t es sencillo. Sólo necesitamos calcular la otra coordenada basándonos en tal valor de t. Por ejemplo, si queremos determinar la intersección de un segmento con el arista x_izq del rectángulo de recorte, entonces sabemos la coordenada del punto de intersección x = x_izq. Por lo tanto, tendremos que hallar la coordenada y a través del parámetro t, que calcularíamos previamente.

Ahora bien, ambos parámetros t - calculado del segmento - y t′ de la arista deben yacer en el intervalo [0,1], para considerar el punto (x,y) como interior al rectángulo de recorte. Por consiguiente, aceptamos tal punto de intersección como válido para el recorte del segmento. También debemos considerar el caso de un segmento paralelo a una arista, antes de resolver las ecuaciones.

Concluimos que este método involucra varios cálculos y comprobaciones y que por tanto se considera ineficiente.

Ejemplo

Veamos un ejemplo sencillo para entender este método.

Descripción

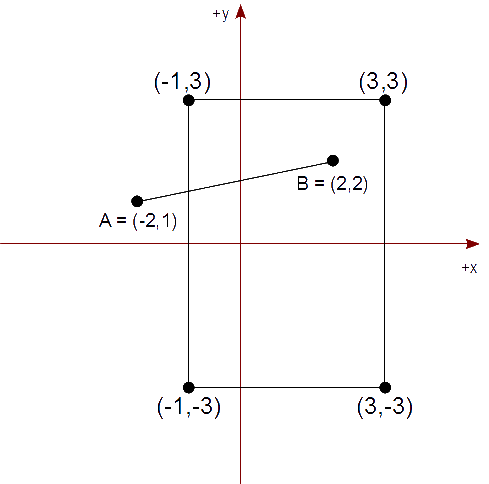
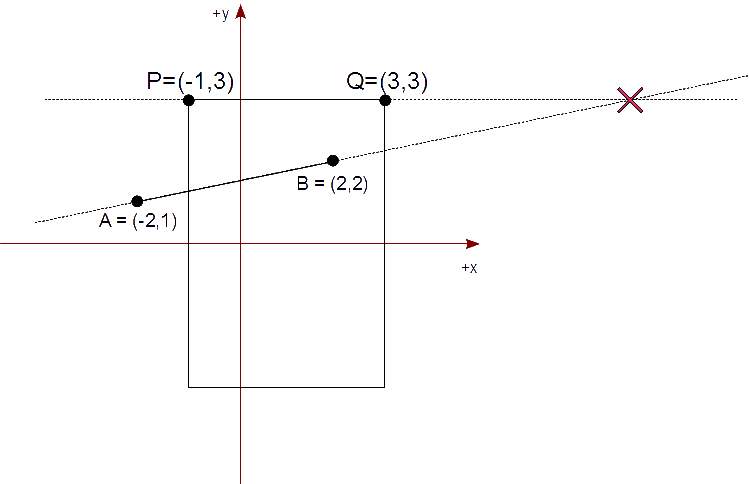
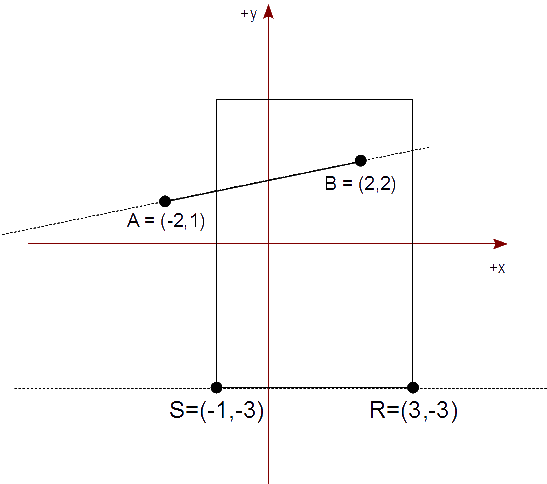
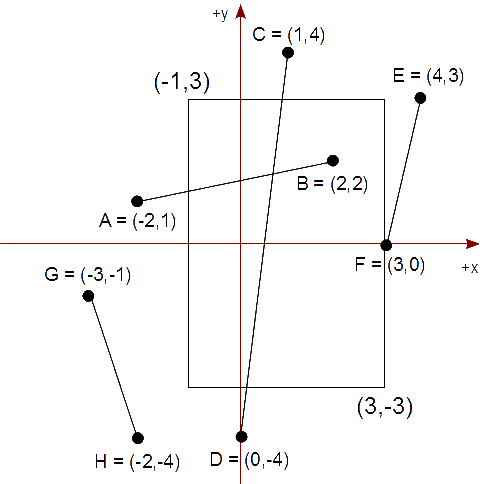
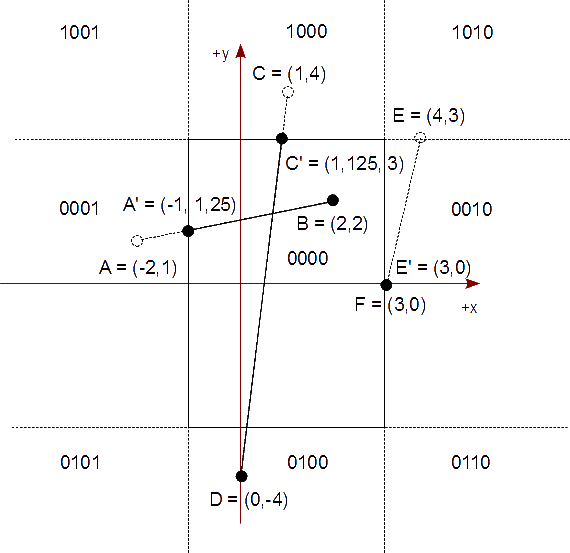
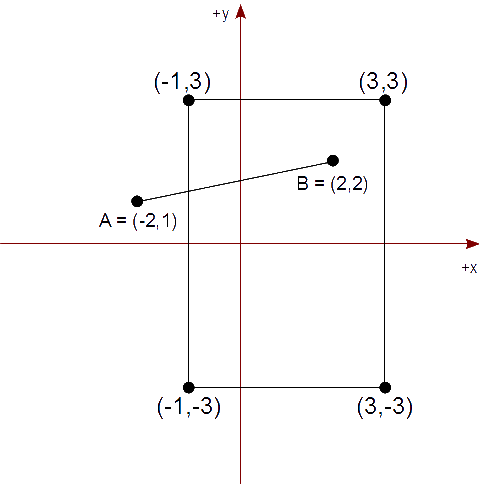
Tenemos un rectángulo de recorte cuya diagonal es de (-1,3) a (3,-3) que representa nuestra vista. Queremos mostrar el segmento AB, en tal rectángulo de recorte, descrito por los puntos,

A = ( -2, 1 )  y   B = ( 2, 2 )

Figura 4 - Intersección con la arista superior

Solución

Comenzamos estableciendo las ecuaciones paramétricas de la línea que contiene el segmento AB y la que contiene la arista superior PQ del rectángulo de recorte,

{ x  = A_x + t (B_x - A_x)
{ y  = A_y + t (B_y - A_y)

{ x′ = P_x + t′ (Q_x - P_x)
{ y′ = P_y + t′ (Q_y - P_y)

Esto quedaría así:

{ x  = -2 + 4 t
{ y  =  1 +   t

{ x′ = -1 + 4 t′
{ y′ =  3 + 0 t′

Como (x,y) = (x′,y′), calculamos t y t′:

{ -2 + 4 t = -1 + 4 t′
{  1 +   t =  3

Dando,

t  = 3 - 1 = 2
t′ = 7 / 4 = 1,75

Como ninguno de estos valores queda comprendido entre 0 y 1, no calculamos el punto de intersección porque no pertenece a ambos segmentos AB ni PQ.

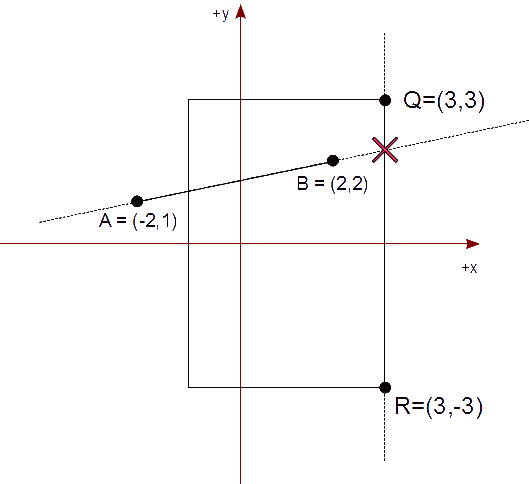
Figura 5 - Intersección con la arista derecha

Establecemos las ecuaciones paramétricas de la línea que contiene el segmento AB y la que contiene la arista derecha QR del rectángulo de recorte.

{ x′ = Q_x + t′ (R_x - Q_x)
{ y′ = Q_y + t′ (R_y - Q_y)

Esto quedaría así:

{ x  = -2 + 4 t
{ y  =  1 +   t

{ x′ = 3 + 0 t′
{ y′ = 3 - 6 t′

Como (x,y) = (x′,y′), calculamos t y t′:

{ -2 + 4 t =  3
{  1 +   t =  3 - 6 t′

Dando,

t  = 5 / 4 = 1,25
t′ = 1 / 8 = 0,125

Aunque t′ queda comprendido entre 0 y 1, t no, por lo que no calculamos el punto de intersección porque no pertenece a ambos segmentos AB ni QR.

Figura 6 - Intersección con la arista inferior

Establecemos las ecuaciones paramétricas de la línea que contiene el segmento AB y la que contiene la arista inferior RS del rectángulo de recorte.

{ x′ = R_x + t′ (S_x - R_x)
{ y′ = R_y + t′ (S_y - R_y)

Esto quedaría así:

{ x  = -2 + 4 t
{ y  =  1 +   t

{ x′ =  3 - 4 t′
{ y′ = -3 + 0 t′

Como (x,y) = (x′,y′), calculamos t y t′:

{ -2 + 4 t =  3 - 4 t′
{  1 +   t = -3

Dando,

t  = -4
t′ = 21 / 4 = 5,25

Obviamente ninguno de estos valores paramétricos queda comprendido entre 0 y 1, por lo que no calculamos el punto de intersección porque no pertenece a ambos segmentos AB ni RS.

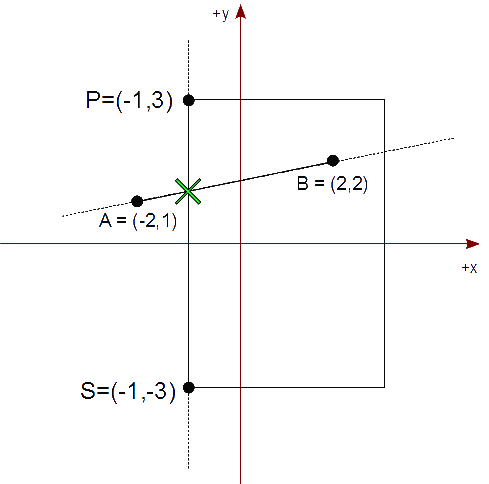
Figura 7 - Intersección con la arista izquierda

Establecemos las ecuaciones paramétricas de la línea que contiene el segmento AB y la que contiene la arista izquierda SP del rectángulo de recorte,

{ x′ = S_x + t′ (P_x - S_x)
{ y′ = S_y + t′ (P_y - S_y)

Esto quedaría así:

{ x  = -2 + 4 t
{ y  =  1 +   t

{ x′ = -1 + 0 t′
{ y′ = -3 + 9 t′

Como (x,y) = (x′,y′), calculamos t y t′:

{ -2 + 4 t = -1
{  1 +   t = -3 + 9 t′

Dando,

t  = 1 / 4 = 0,25
t′ = 4,25 / 9 ≅ 0,4722

Ambos valores paramétricos quedan comprendidos entre 0 y 1, por lo que calculamos el punto de intersección a partir de cualquiera de los dos segmentos. Por ejemplo, usando el segmento AB, volvemos a las ecuaciones paramétricas con el parámetro t = 0,25,

{ x  = -2 + 4 (0,25) = -1
{ y  =  1 +   (0,25) =  1,25

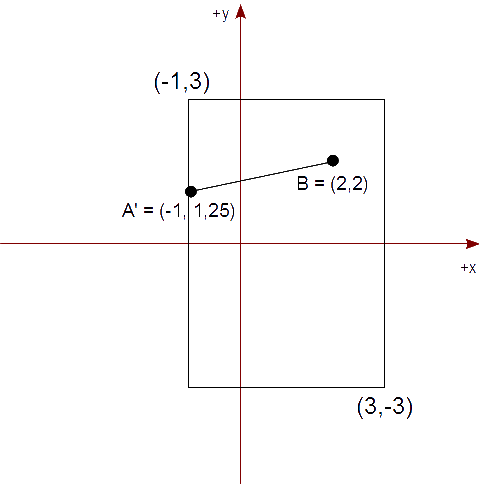
Dando el punto de intersección (-1, 1,25).

Vemos que debemos acortar el segmento AB dando lugar a nuevos valores usando este punto de intersección:

A′ = (-1, 1,25)
B  = ( 2, 2)

Al final, el segmento AB es acortado al segmento A′B.

Algoritmo de Cohen-Sutherland

Este algoritmo realiza varias comprobaciones iniciales para descubrir si se puede evitar cálculos de las intersecciones. El primer paso es comprobar si los puntos extremos del segmento son aceptados por sus posiciones. Si esto no es posible, entonces realizamos varias comprobaciones por regiones exteriores al rectángulo de recorte, formadas por las líneas rectas al extender sus aristas. Asimismo, podemos rechazar un segmento inmediatamente si sus extremos yacen en regiones a la izquierda de x_izq, por encima de y_sup, a la derecha de x_der, y por debajo de _inf.

Si el segmento no se puede aceptar ni rechazar inmediatamente, entonces es partido en dos segmentos por un arista del rectángulo de recorte, para que uno de ellos sea rechazado de inmediato. Esto implica que implementamos un método iterativo de recorte para el segmento hasta que éste sea aceptado o rechazado. Este algoritmo es eficiente especialmente en el caso de tener un rectángulo de recorte muy grande que comprende a todos o una gran mayoría de los segmentos a visualizar. Asimismo, podemos tener el caso de un rectángulo de recorte muy pequeño que fuerza a todos o casi todos los segmentos a ser rechazados.

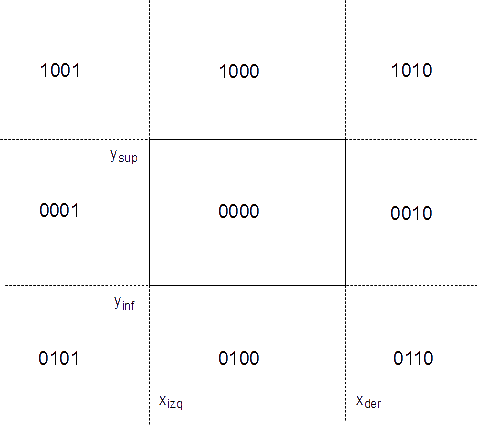
Se le asigna un código de cuatro bits, b₃b₂b₁b₀, a cada región de las nueve creadas. Este código binario es creado estratégicamente para representar rápida y fácilmente cada región. El valor de 1 indicará que un extremo yace en tal región mientras que un 0 indicará lo contrario.Aquí tenemos la estrategia a usar:

Bit	Condición	Descripción
b₃	y > y_sup	por encima de la arista superior
b₂	y < y_inf	por debajo de la arista inferior
b₁	x > x_der	a la derecha de la arista derecha
b₀	x < x_izq	a la izquierda de la arista izquierda

Figura 9 - Las regiones con los Códigos del Algoritmo de Cohen-Sutherland

Usaremos ciertas operaciones a nivel de bit para asignar el código regional a cada extremo en el que yace y también para determinar tal región cuando necesitemos discriminarlos. Una forma eficiente de asignar un valor a un bit particular es tomando el primer bit que indica el signo positivo o negativo de la resta entre las dos coordenadas de la condición. Esto es, b₃ es asignado el bit del signo de (y_sup-y), b₂ es asignado el bit de (y - y_inf), b₁ es asignado el bit de (x_sup-x), y b₀ es asignado el bit de (x - x_inf).

La figura 9 muestra las regiones con sus correspondientes códigos.

Con estos códigos podemos determinar si los extremos, y por tanto el segmento que representan, pueden ser aceptados o rechazados inmediatamente. Obviamente, si ambos códigos son 0, entonces ambos extremos existen dentro del rectángulo de recorte, y por consiguiente el segmento es aceptado de inmediato. Para combinar estos dos códigos, simplemente aplicamos una operación OR y comprobamos si el resultado es 0. Si el código no es 0, entonces aplicamos la operación AND a ambos códigos. Si el resultado no es cero, entonces rechazamos el segmento de inmediato.

Si no podemos aceptar ni rechazar inmediatamente el segmento, entonces iremos dividiendo el segmento y comprobando sus nuevos códigos, para determinar su aceptación o rechazo. Dividimos el segmento calculando la intersección con las líneas creadas al extender las aristas del rectángulo de recorte. Si no podemos discriminar el nuevo segmento, entonces debemos continuar dividiéndolo hasta que al final lo aceptamos o lo rechazamos. Una propiedad notable es que modificamos el segmento mudando el extremo, cuyo código no es cero. Dicho de otra manera, el algoritmo elige un extremo exterior que será mudado a la intersección con la arista o con la línea que separa y define las regiones. Asignamos el código regional del punto de intersección al extremo mudado.

La desventaja de este algoritmo es que puede realizar varias intersecciones antes de alcanzar la intersección final y válida. Una mejora es calcular la pendiente para determinar el punto de intersección una sola vez y conservarla para posteriores iteraciones. Aun con esta mejora, este algoritmo no es tan eficiente. Por otro lado, la ventaja de este algoritmo es su simplicidad y además se puede extender fácilmente al caso de un volumen de recorte en 3D.

Ejemplo

Descripción

Queremos mostrar varios segmentos, pero únicamente dentro de nuestra vista representada por un rectángulo vertical descrito con las siguientes esquinas: superior izquierda (-1,3) e inferior derecha (3,-3). Tenemos los siguientes segmentos definidos por parejas de puntos que forman sus extremos:
A = (-2, 1) y B = ( 2, 2),
C = ( 1, 4) y D = ( 0,-4),
E = ( 4, 3) y F = ( 3, 0),
G = (-3,-1) y H = (-2,-4).

Solución

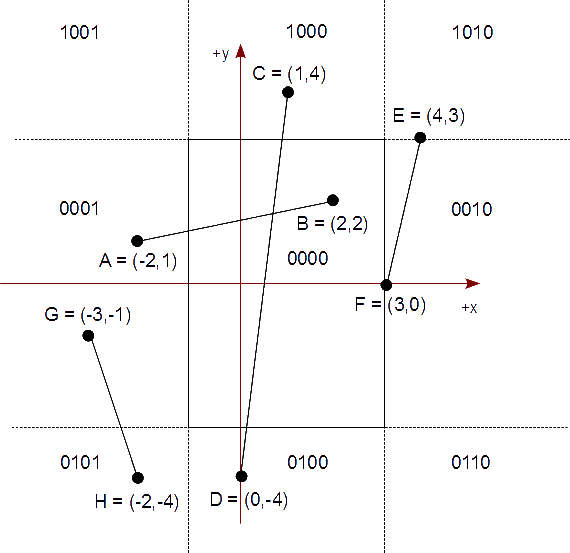
Calculamos los códigos regionales para cada punto:

A: 0001  B: 0000
C: 1000  D: 0100
E: 0010  F: 0000
G: 0001  H: 0101

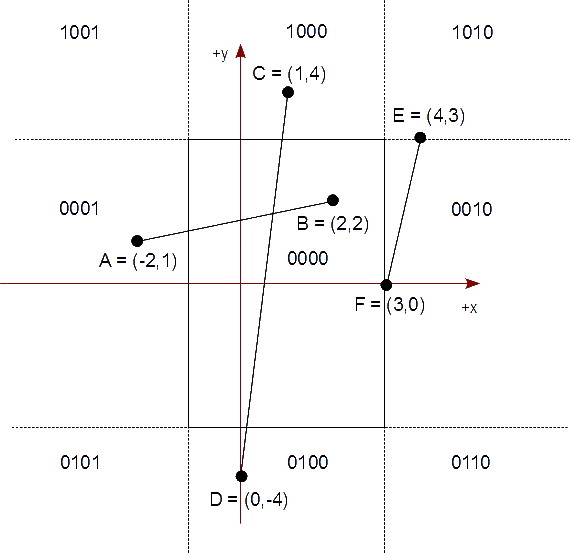
Figura 12 - Ejemplo Solución Aplicando Criterios

Aplicamos nuestros criterios a los resultados de las operaciones a nivel de bit de los códigos regionales de cada punto dando lugar a:


AB: 0001 OR 0000 = 0001  ⇒  0001 AND 0000 = 0000  ⇒  Hay que recortar
CD: 1000 OR 0100 = 1100  ⇒  1000 AND 0100 = 0000  ⇒  Hay que recortar
EF: 0010 OR 0000 = 0010  ⇒  0010 AND 0000 = 0000  ⇒  Hay que recortar
GH: 0001 OR 0101 = 0101  ⇒  0001 AND 0101 = 0001  ⇒  Inmediatamente lo rechazamos

Figura 13 - Ejemplo Solución Recortando con las Primeras Aristas

Hacemos la primera tanda de recortes de los puntos con sus primeras aristas del algoritmo, obteniendo:

{ A'_x = -1
{ A'_y =  1 + 1 * 1 / 4 = 1,25

{ C'_x =  1 - 1 * 1 / (-8) = 1,125
{ C'_y =  3

{ E'_x =  3
{ E'_y =  3 - 3 * (-1) / (-1) = 0

Recalculamos los códigos de cada punto:

A′B: 0000 OR 0000 = 0000  ⇒  Aceptamos el segmento
C′D: 0000 OR 0100 = 0100  ⇒  0000 AND 0100 = 0000  ⇒  Hay que recortar
E′F: 0000 OR 0000 = 0000  ⇒  Aceptamos el segmento

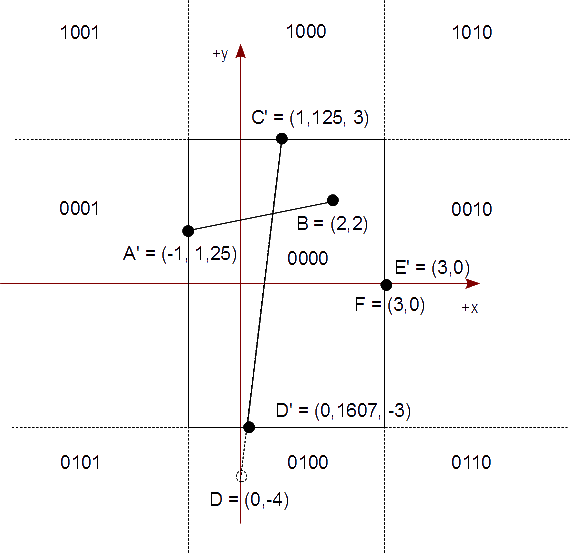
Figura 14 - Ejemplo Solución Recortar C′D

Nos falta recortar una segunda vez para el segmento C′D. El algoritmo elige el punto D para recortar, obteniendo:

{ D'_x =  0 + 1,125 * 1 / 7 = 0,1607
{ D'_y = -3

Recalculamos los códigos de cada punto:

C′D′: 0000 OR 0000 = 0000  ⇒  Aceptamos el segmento

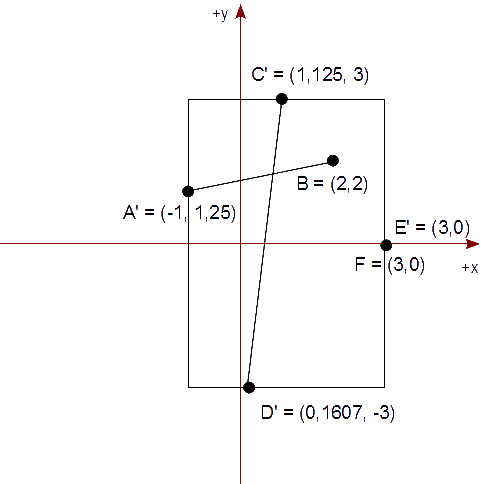
Al final, obtenemos la siguiente imagen con los segmentos recortados e interiores al rectángulo de recorte.

Algoritmo

Para Recortar(), el algoritmo es:

booleano Recortar( ref Punto P, ref Punto Q, Rectángulo R )
	1. aceptar ← falso
	2. terminar ← falso
	3. códigoP ← Calcular_Código(P,R)
	4. códigoQ ← Calcular_Código(Q,R)
	5. Repetir:
		6. Si (códigoP OR códigoQ) = 0, entonces
			7. aceptar ← verdadero
			8. terminar ← verdadero
		9. Si no, compruebe que  (códigoP AND códigoQ) ≠ 0,
			10. terminar ← verdadero
		11. Si no, entonces
			12. Si códigoP = 0, entonces
				13. código ← códigoQ
			14. Si no, entonces
				15. código ← códigoP
			16. Si código es SUPERIOR, entonces
				17. Δy ← Q.y-P.y
				18. Si Δy = 0, entonces  // segmento vertical
					19. x ← P.x
				20. Si no, entonces
					21. x ← P.x + (Q.x-P.x)*(R.y_sup-P.y) / Δy
				22. y ← y_sup
			23. Si no, compruebe que código es INFERIOR
				24. Δy ← Q.y-P.y
				25. Si Δy = 0, entonces  // segmento vertical
					26. x ← P.x
				27. Si no, entonces
					28. x ← P.x + (Q.x-P.x)*(R.y_inf-P.y) / Δy
				29. y ← y_inf
			30. Si no, compruebe que código es DERECHA
				31. x ← x_der
				32. y ← P.y + (Q.y-P.y)*(R.x_der-P.x) / (Q.x-P.x)
			33. Si no, entonces  // código = IZQUIERDA
				34. x ← x_izq
				35. y ← P.y + (Q.y-P.y)*(R.x_izq-P.x) / (Q.x-P.x)
			36. Si código = códigoP, entonces
				37. P.x ← x
				38. P.y ← y
				39. códigoP ← Calcular_Código(P,R)
			40. Si no, entonces
				41. Q.x ← x
				42. Q.y ← y
				43. códigoQ ← Calcular_Código(Q,R)
	44. Mientras que terminar = falso
	45. Terminar( aceptar )

Si el segmento es aceptado, entonces el algoritmo terminará con el valor booleano verdadero. Además, los extremos, P y Q, contendrán los valores recortados por este mismo algoritmo. Si el segmento es rechazado, entonces uno debería hacer caso omiso de los parámetros, P y Q. En cualquier caso, se pasan estos dos parámetros por referencia, para así poder modificarlos.

A continuación presentamos el algoritmo para Calcular_Código(), el cual requiere un punto, P, y el rectángulo de recorte, R:

entero Calcular_Código( Punto P, Rectángulo R )
	1. código ← 0
	2. Si P.y > R.y_sup, entonces
		3. código ← código OR SUPERIOR
	4. Si no, compruebe que P.y < R.y_inf
		5. código ← código OR INFERIOR
	6. Si P.x > R.x_der, entonces
		7. código ← código OR DERECHA
	8. Si no, compruebe que P.x < R.x_izq
		9. código ← código OR IZQUIERDA
	10. Terminar( código )

No todos los lenguajes de programación aceptan realizar operaciones a nivel de bit con números que no sean enteros. Tampoco todos los lenguajes establecen exactamente la cantidad de bits para representar internamente un número real. Por estas razones, no hemos presentado el algoritmo mejorado para Calcular_Código() que previamente hablamos en este apartado.

Suponiendo que un número real se representase con 32 bits y el 32º bit contiene su signo positivo, como 0, o negativo, como 1, aquí presentamos otra versión del algoritmo Calcular_Código():

entero Calcular_Código( Punto P, Rectángulo R )
	1. código ← (((P.y - R.y_sup) SHR 31) SHL 3) OR 
		(((R.y_inf - P.y) SHR 31) SHL 2) OR
        (((P.x - R.x_der) SHR 31) SHL 1) OR
        ((R.x_izq - P.x)  SHR 31)
	2. Terminar( código )

El operador SHL se refiere a la operación común de desplazamiento de bits a la izquierda y el operador SHR se refiere a la del desplazamiento de bits a la derecha.

Algoritmo de Cyrus-Beck

Figura 16 - Tres ejemplos de puntos fuera, dentro, y en la arista de la región de recorte

Este algoritmo se basa en calcular las intersecciones del segmento, P₀P₁, con cada arista de un polígono convexo de recorte. Se usa la ecuación paramétrica de la línea para determinar los cuatro valores de t. Posteriormente, realizamos varias comparaciones para determinar cuáles de estos cuatro valores de t corresponden a intersecciones reales. Sólo al tener los valores válidos de t es cuando calculamos los puntos de intersección. Para encontrar el punto de intersección, el algoritmo de Cyrus-Beck se basa en la ecuación paramétrica de una línea recta. Como tenemos dos segmentos: P₀P₁ y la arista, que yacen sobre dos líneas rectas, tenemos dos ecuaciones paramétricas que las representan. Al resolver estas dos ecuaciones, averiguaremos un valor de t con el que determinaremos el punto de intersección. La ecuación paramétrica es la siguiente:
P(t) = P₀ + (P₁-P₀) t
donde t queda comprendido en el intervalo [0,1]. Esto implica que P(0) = P₀ y P(1) = P₁.

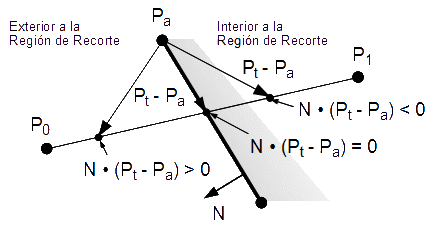
Para determinar el valor exacto de t, haremos uso del producto escalar entre dos vectores. El primer vector será el vector normal de la arista que apunta hacia fuera de la región de recorte. El segundo vector será uno que coincide con la arista. Crearemos este segundo vector a partir de un punto cualquiera, P_a, en la arista, y el punto P(t) que es común a la línea del segmento, P₀P₁, que queremos recortar y a esta misma arista. El cálculo es el siguiente:
N⋅(P(t) - P_a)

Si el producto escalar es positivo, entonces el punto, P(t), yace fuera de la región de recorte y si es negativo, entonces P(t) yace dentro. Como nos interesa averiguar el punto común que yace en la arista y por tanto el borde de la región de recorte, el producto escalar debe ser 0; véase la figura 16. Esto significa que debemos resolver la siguiente ecuación:
N⋅(P(t) - P_a) = 0

Sustituimos P(t) por su definición,
N⋅(P₀ + (P₁-P₀) t - P_a) = 0

Aplicamos la propiedad distributiva,
N⋅(P₀ - P_a) + N⋅(P₁-P₀) t = 0

Dejemos que D = P₁-P₀, que es el vector de P₀ a P₁ del segmento. Ahora resolvemos para t:

     N⋅(P₀ - P_a) 
t = ------------
        -N⋅D

Este valor de t es válido solamente si el denominador no es cero. Esto significa que las siguientes condiciones deben mantenerse:

N ≠ 0	El vector normal jamás debería ser nulo. Si ocurriere lo contrario, entonces se trata de un error.
D ≠ 0	Esto significa que P₀ ≠ P₁. Si ocurriere lo contrario, entonces se trata de un solo punto y no de un segmento.
N⋅D ≠ 0	Esto significa que la arista y el segmento no son paralelos. Si fueren paralelos, entonces no existe ninguna intersección.

El algoritmo calcula cada intersección entre el mismo segmento y cada arista de la región de recorte. Para este cálculo, determinamos el vector normal de cada arista y un punto arbitrario que yace en una arista. Lo más sencillo y práctico es elegir un punto conocido como un vértice que forma la arista. Posteriormente, debemos elegir cuáles de los cuatro valores de t corresponden a intersecciones internas a la región de recorte. Primeramente, comprobamos que los valores de t quedan comprendidos en el intervalo [0,1]. Si no se cumple esta condición, entonces significa que el punto de intersección no yace en el segmento y por tanto descartamos tal valor de t. Como cada cálculo que hacemos se basa en encontrar las intersecciones entre dos líneas rectas, esto significa que un valor de t puede indicar una intersección que no yace en una arista.

En algunos casos, no es tan sencillo determinar si una intersección yace dentro o fuera de la región de recorte. Podríamos realizar varias comprobaciones, pero entonces ralentizaríamos el algoritmo y no conseguiríamos una ventaja sobre otros algoritmos, como el de Cohen-Sutherland. Analizando varios casos de intersecciones entre segmentos y aristas, descubrimos un comportamiento que nos servirá para discriminar tal intersección y así determinar si es aceptada o rechazada. Esta técnica se basa en denominar las intersecciones como potencialmente entrantes (PE) y potencialmente salientes (PS) de la región de recorte. Si cruzamos una arista, yendo desde los extremos P₀ a P₁, que nos hace entrar en la mitad del plano, entonces la intersección lleva la etiqueta de PE. Si por el contrario, al cruzar la arista, nos hace salir del plano interior creado por la arista, entonces tal intersección es PS. Con esta clasificación, notamos que dos intersecciones interiores a la región de recorte tienen etiquetas opuestas.

Para clasificar si una intersección es PE o PS, podemos basarnos en el ángulo formado por los vectores del segmento P₀P₁ y el normal de una arista. Si el ángulo es mayor de 90°, entonces es PE; y si es menor de 90°, entonces es PS. No requerimos calcular el ángulo, ya que esta información está contenida en el producto escalar del vector normal N y el vector D del segmento P₀P₁:

N⋅D < 0	⇒ ángulo > 90°	⇒ PE
N⋅D > 0	⇒ ángulo < 90°	⇒ PS

Vemos que N⋅D es el denominador en el cálculo de t para determinar el punto de intersección. Por lo tanto, podemos clasificar el valor de t mientras lo calculamos.

Nos interesa encontrar aquellos puntos de intersección etiquetados de PE a PS. El punto de intersección con la etiqueta PE que sea interior a la región de recorte es aquél que tenga el mayor valor de t; lo llamaremos, t_e. El punto interior que tenga la etiqueta PS es aquél que tenga el menor valor de t, al cual lo llamaremos, t_s. El segmento cruzante se define en el intervalo [t_e,t_s]. Como ya mencionamos anteriormente, los valores de t deben estar comprendidos en el intervalo de [0,1]. Por consiguiente, la cota inferior de t_e = 0 y la cota superior de t_s = 1. Si t_e > t_s, entonces el segmento no es interior a la región de recorte y por tanto lo rechazamos. Al final, obtendremos los valores correctos de t_e y t_s para así calcular las coordenadas x e y de los puntos de intersección.

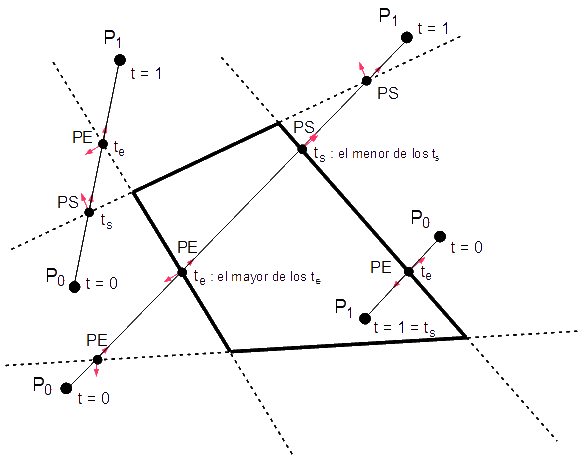
Figura 17 - Tres casos de segmentos cruzando las aristas del polígono de recorte con las etiquetas PE y PS

Este algoritmo tiene la ventaja de no estar basado en un bucle comparado con el algoritmo de Cohen-Sutherland.

Ejemplo

Descripción

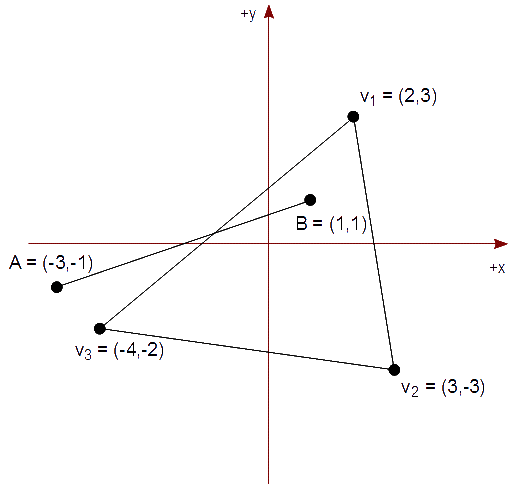
Queremos mostrar un segmento, pero únicamente dentro de nuestra vista representada por un triángulo descrito con los siguientes vértices: { (2,3), (3,-3), (-4,-2) }. Tenemos un segmento definido por la siguiente pareja de sus puntos extremos:

A = (-3,-1) y B = (1,1)

Solución

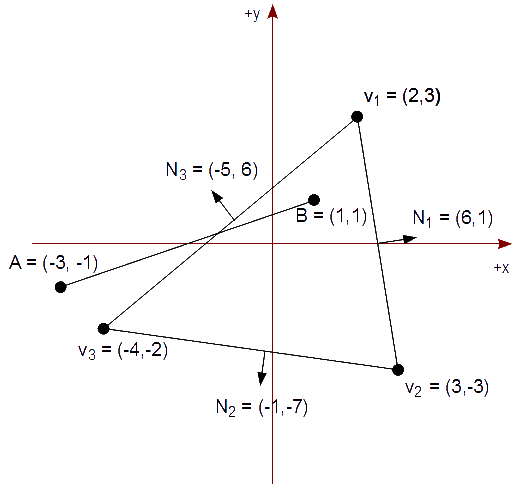
Figura 19 - Calculamos los vectores normales de cada arista

Calculamos los vectores normales - sin normalizar - de todas las aristas de nuestro triángulo de recorte:

v₁₂ = (  3, -3 ) - (  2,  3 ) = (  1, -6 )  ⇒  N₁ = (  6,  1 )
v₂₃ = ( -4, -2 ) - (  3, -3 ) = ( -7,  1 )  ⇒  N₂ = ( -1, -7 )
v₃₁ = (  2,  3 ) - ( -4, -2 ) = (  6,  5 )  ⇒  N₃ = ( -5,  6 )

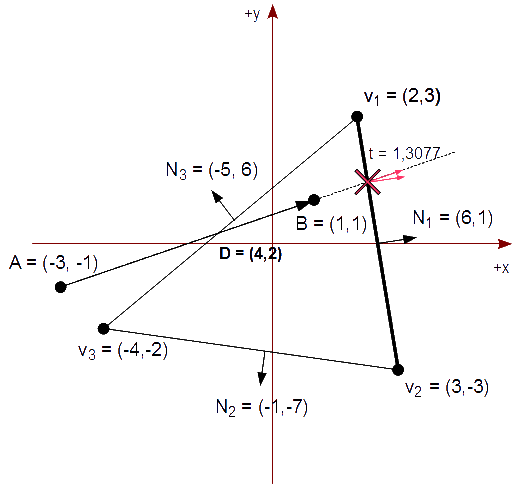
Figura 20 - Calculamos y etiquetamos t para la primera intersección

Calculamos el valor de t para la intersección de la línea que contiene el segmento AB con la línea generada por v₁v₂. Primero calculamos y comprobamos el denominador del cálculo de t por si es 0 y por tanto el segmento es paralelo a la arista:

N₁⋅D = (  6,  1 ) ⋅ (  4,  2 ) = 6*4 + 1*2 = 26

Como el denominador no es 0, calculamos el valor de t para t_s ya que el denominador es positivo por lo que se trata de un punto potencialmente saliente:

     (  6,  1 ) ⋅ (( -3, -1 ) - (  2,  3 ))
t = ---------------------------------------- 
                     -26

     (  6,  1 ) ⋅ ( -5, -4 )
  = -------------------------
               -26

     6*(-5) + 1*(-4)     -34
  = ----------------- = ----- = 1,3077
            -26          -26

Como el valor de t no queda comprendido en [0,1], lo descartamos. El valor de t_s sigue siendo 1, en estos momentos, ya que queremos el menor valor para t_s. Esto es correcto, ya que 1 < 1,3077.

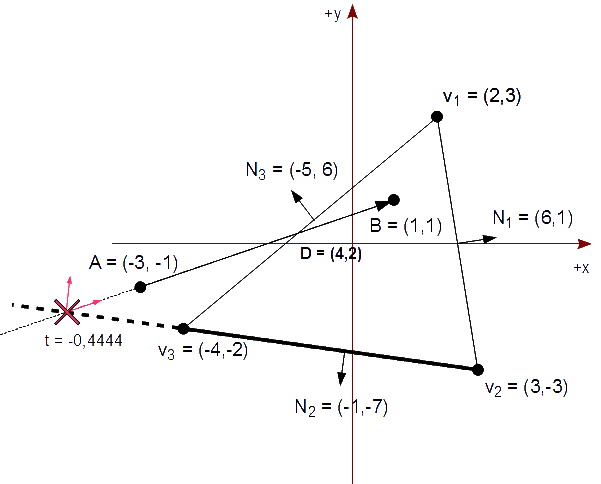
Figura 21 - Calculamos y etiquetamos t para la segunda intersección

Calculamos el valor de t para la intersección de la línea que contiene el segmento AB con la línea generada por v₂v₃. Primero calculamos y comprobamos el denominador del cálculo de t por si es 0 y por tanto el segmento es paralelo a la arista:

N₂⋅D = ( -1, -7 ) ⋅ (  4,  2 ) = (-1)*4 + (-7)*2 = -18

Como el denominador no es 0, calculamos el valor de t para t_e ya que el denominador es negativo por lo que se trata de un punto potencialmente entrante:

     ( -1, -7 ) ⋅ (( -3, -1 ) - (  3, -3 ))
t = ---------------------------------------- 
                   -(-18)

     ( -1, -7 ) ⋅ ( -6,  2 )
  = -------------------------
               18

     (-1)*(-6) + (-7)*2     -8
  = -------------------- = ---- = -0,4444
             18             18

Como el valor de t no queda comprendido en [0,1], lo descartamos. El valor de t_e sigue siendo 0, en estos momentos, ya que queremos el mayor valor para t_e. Esto es correcto, ya que -0,4444 < 0.

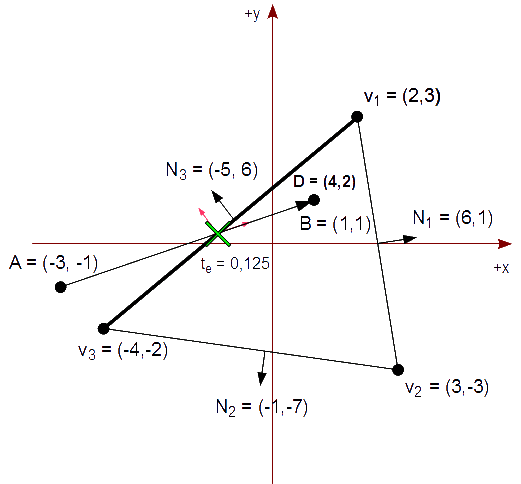
Figura 22 - Calculamos y etiquetamos t para la tercera intersección

Calculamos el valor de t para la intersección de la línea que contiene el segmento AB con la línea generada por v₃v₁. Primero calculamos y comprobamos el denominador del cálculo de t por si es 0 y por tanto el segmento es paralelo a la arista:

N₃⋅D = ( -5,  6 ) ⋅ (  4,  2 ) = (-5)*4 + 6*2 = -8

Como el denominador no es 0, calculamos el valor de t para t_e ya que el denominador es negativo por lo que se trata de un punto potencialmente entrante:

     ( -5,  6 ) ⋅ (( -3, -1 ) - ( -4, -2 ))
t = ---------------------------------------- 
                     -(-8)

     ( -5,  6 ) ⋅ (  1,  1 )
  = -------------------------
                8

     (-5)*1 + 6*1     1
  = -------------- = --- = 0,125
           8          8

Como el valor de t queda comprendido en [0,1], actualizamos el valor de t_e para que sea 0,125, ya que 0,125 > 0, su valor anterior.

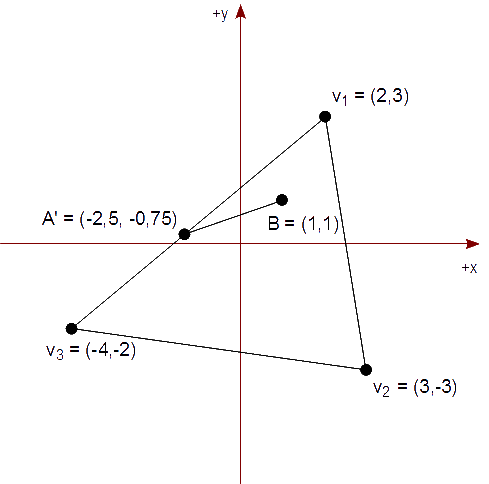
Al terminar de inspeccionar todas las aristas del triángulo de recorte, comprobamos los valores de t_e y t_s, ya que son las cotas inferior y superior, respectivamente, de un intervalo: t_e ≤ t_s. En nuestro caso, obtenemos el siguiente intervalo válido: [0,125, 1].

Pasamos a calcular los nuevos puntos extremos para el segmento recortado:

A′ = ( -3, -1 ) + (( -3, -1 ) - ( 1, 1 )) * 0,125
   = ( -3, -1 ) + (  4,  2 ) * 0,125
   = ( -3 + 0,5, -1 + 0,25 )
   = ( -2,5, -0,75 )

B′ = ( -3, -1 ) + (( -3, -1 ) - ( 1, 1 )) * 1
   = ( -3, -1 ) + ( 4, 2 ) * 1
   = ( -3 + 4, -1 + 2 )
   = (  1,  1 )

Algoritmo

Tenemos varias funciones a destacar para implementar este algoritmo:

La función principal es Recortar(), la cual aceptará tres parámetros: dos puntos extremos, P y Q, donde cada uno contiene las coordenadas (x,y) que representan el segmento a recortar, y un polígono convexo, R, que contiene una lista de vértices {v₁, v₂, v₃, ..., v_n} en el sentido de las agujas del reloj para representar la región de recorte.
La función Recortar_Punto() se invocará para tratar el segmento como un único punto. Básicamente, se realizará el algoritmo explicado anteriormente.
La función Calcular_Normal() es necesaria si no tenemos una lista de normales de las aristas del polígono de recorte, R.
Las funciones mayor() y menor() determinan cuáles de los dos parámetros dados son el mayor y el menor, respectivamente.
La función Calcular_Punto() sirve para obtener un punto en una línea recta según la ecuación paramétrica. Esta función requiere dos puntos extremos de la línea y el parámetro, t.

Para Recortar(), el algoritmo es:

booleano Recortar( ref Punto P, ref Punto Q, PolígonoConvexo R )
	1. Si P = Q, entonces
		2. resultado ← Recortar_Punto( P, R )
		3. Terminar( resultado )
	4. Si no, entonces
		5. t_e ← 0
		6. t_s ← 1
		7. Para cada vértice, v_i, de R, hacer
			8. N ← Calcular_Normal( v_i+1 - v_i )
			9. numerador ← N⋅(P - v_i)
			10. denominador ← -N⋅(Q - P)
			11. Si denominador ≠ 0, entonces
				12. t ← numerador / denominador
				13. Si denominador < 0, entonces
					14. t_e ← mayor( t_e, t )
				15. Si no, entonces
					16. t_s ← menor( t_s, t )
			17. Si no, compruebe que numerador > 0,
				18. Terminar( falso )
		19. Si t_e > t_s, entonces
			20.Terminar( falso )
		21. Si no, entonces
			22. P_e ← Calcular_Punto( P, Q, t_e )
			23. P_s ← Calcular_Punto( P, Q, t_s )
			24. P ← P_e
			25. Q ← P_s
	26. Terminar( verdadero )

Si el segmento es aceptado, entonces el algoritmo terminará con el valor booleano verdadero. Además, los extremos, P y Q, contendrán los valores recortados por este mismo algoritmo. Si el segmento es rechazado, el algoritmo termina con el valor falso, lo cual implica que los parámetros, P y Q, no son alterados. En cualquier caso, se pasan estos dos parámetros por referencia, para así poder modificarlos.

A continuación presentamos el algoritmo para Calcular_Normal(), el cual requiere un vector, v:

Vector Calcular_Normal( Vector v )
	1. vector N ← ( -v.y, v.x )
	2. N ← Normalizar( N )
	3. Terminar( N )

Este cálculo nos sirve si el vector dado sigue el convenio de ir en el sentido de las agujas del reloj. La función Normalizar() se refiere a la operación vectorial para convertir un vector en unitario. Sin embargo, en este algoritmo, no es necesario normalizar estos vectores normales, por lo que podemos conseguir una optimización para el algoritmo de Cyrus-Beck.

Por último, tenemos el algoritmo para Calcular_Punto(), que requiere dos puntos, P y Q, y un valor para t:

Punto Calcular_Punto( Punto P, Punto Q, real t )
	1. Punto A ← P + (Q-P) t
	2. Terminar( A )

Algoritmo de Liang-Barsky

Este algoritmo se basa en el algoritmo propuesto por Cyrus-Beck. La diferencia es que el algoritmo de Liang-Barsky aplica ciertas interpretaciones geométricas y simplificaciones al basarse en un rectángulo vertical de recorte. Con un rectángulo vertical, podemos definir los vectores normales sin problemas al igual que los vectores en las aristas. Veamos una tabla de ciertos valores y las simplificaciones que podemos realizar.

Arista de Recorte	Normal, N	Vértice, V	P₀-V	D = P₁-P₀	t = -N⋅(P₀ - V) / N⋅D
izquierda: x = x_izq	(-1,0)	(x_izq, V_y)	(x₀-x_izq, y₀-V_y)	(x₁-x₀, y₁-y₀)	-(x₀-x_izq) / (x₁-x₀)
derecha: x = x_der	(1,0)	(x_der, V_i.y)	(x₀-x_der, y₀-V_y)	(x₁-x₀, y₁-y₀)	(x₀-x_der) / -(x₁-x₀)
superior: y = y_sup	(0,-1)	(V_i.x, y_sup)	(x₀-V_x, y₀-y_sup)	(x₁-x₀, y₁-y₀)	-(y₀-y_sup) / (y₁-y₀)
inferior: y = y_inf	(0,1)	(V_i.x, y_inf)	(x₀-V_x, y₀-y_inf)	(x₁-x₀, y₁-y₀)	(y₀-y_inf) / -(y₁-y₀)

Según esta tabla, vemos que el cálculo de t se reduce a una división de distancias entre coordenadas homogéneas: anchuras para el recorte de las coordenadas en X y alturas para el recorte de las coordenadas en Y. El numerador pasa a ser la distancia del punto extremo del segmeneto a la arista. Esta distancia equivale a la misma cantidad que usamos en el método de Cohen-Sutherland al calcular el código binario para cada punto extremo. También podemos ver que el denominador es la anchura, dx, o la altura, dy. Según el signo de estas longitudes, el segmento es PE o PS, y por ello los signos del numerador y del denominador se deben conservar, para que el algoritmo funcione correctamente.

Ejemplo

Descripción

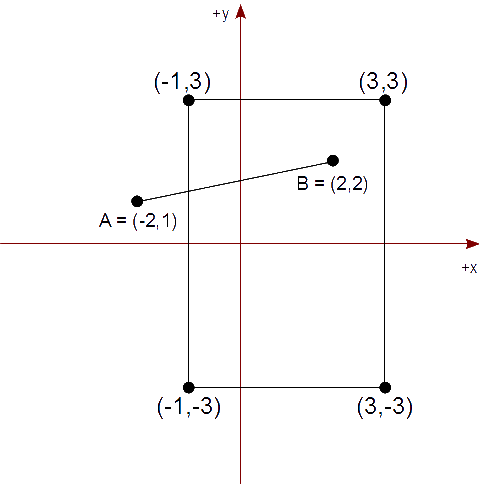
Retomamos el mismo ejemplo del método exhaustivo. Tenemos un rectángulo de recorte cuya diagonal es de (-1,3) a (3,-3) que representa nuestra vista. Queremos mostrar el segmento AB, en tal rectángulo de recorte, descrito por los puntos,

A = ( -2, 1 )  y  B = ( 2, 2 )

Solución

Figura 25 - Calculamos t[e] y t[s] para la intersección con la arista izquierda

Calculamos el vector D de A a B:

D = B - A = (  2,  2 ) - ( -2,  1 ) = (  4,  1 )

Comprobamos el caso trivial en el que los dos puntos representan un mismo punto visible, en lugar de un segmento. Como D ≠ (0,0), tenemos un segmento.

Calculamos la intersección del segmento AB con la arista izquierda. Como el denominador, D_x = 4, es positivo, calculamos t:

     R.x_izq - A_x    -1 - (-2)    1
t = ------------ = --------- = --- = 0,25
          D_x           4        4

Como t > t_e, actualizamos t_e = 0,25. El intervalo de t por ahora es [0,25, 1].

Figura 26 - Calculamos t[e] y t[s] para la intersección con la arista derecha

Calculamos la intersección del segmento AB con la arista derecha. Usamos el denominador, -D_x = -4, que al ser negativo, calculamos t:

     A_x - R.x_der     -2 - 3     -5
t = ------------ = -------- = ---- = 1,25
         -D_x          -4       -4

Como t > t_s, no actualizamos t_s. El intervalo de t por ahora sigue siendo [0,25, 1].

Figura 27 - Calculamos t[e] y t[s] para la intersección con la arista inferior

Calculamos la intersección del segmento AB con la arista inferior. Usamos el denominador, D_y = 1, que al ser positivo, calculamos t:

     R.y_inf - A_y     -3 - 1
t = ------------ = -------- = -4
          D_y           1

Como t < t_e, no actualizamos t_e. El intervalo de t por ahora sigue siendo [0,25, 1].

Figura 28 - Calculamos t[e] y t[s] para la intersección con la arista superior

Calculamos la intersección del segmento AB con la arista superior. Usamos el denominador, -D_y = -1, que al ser negativo, calculamos t:

     A_y - R.y_sup     1 - 3
t = ------------ = ------- = 2
         -D_y          -1

Como t > t_s, no actualizamos t_s. El intervalo de t por ahora sigue siendo [0,25, 1].

Figura 29 - Calculamos los puntos extremos a partir de t[e] y t[s]

Como t_s no fue actualizado, no necesitamos que realizar ningún cálculo. Como t_e fue actualizado, calculamos el punto entrante de intersección, A:

A′ = A + t_e * ( D_x, D_y ) 
   = ( -3,  1 ) + 0,25 * (  4,  1 ) 
   = ( -2,  1,25 )

Algoritmo

Tenemos varias funciones a destacar para implementar este algoritmo:

La función principal es Recortar(), la cual aceptará tres parámetros: dos puntos extremos, P y Q, donde cada uno contiene las coordenadas (x,y) que representan el segmento a recortar, y un rectángulo vertical, R, que contiene los elementos {x_izq,y_sup, x_der,y_inf} representando las coordenadas de las dos esquinas izquierda superior y derecha inferior.
La función Recortar_Punto() se invocará para tratar el segmento como un único punto. Básicamente, se realizará el algoritmo explicado anteriormente. El resultado es un valor booleano que indicará si el punto fue recortado (verdadero) o no (falso).
La función Calcular_Parámetros() servirá para calcular los parámetros, t_e y t_s. Necesitamos pasar el numerador, el denominador, y los parámetros, t_e y t_s, que serán modificados. Esta función nos indicará si estos parámetros, t_e y t_s, han sido modificados y por tanto, el segmento es aceptado (verdadero) o rechazado (falso).

Para Recortar(), el algoritmo es:

booleano Recortar( ref Punto P, ref Punto Q, Rectángulo R )
	1. dx ← Q.x - P.x
	2. dy ← Q.y - P.y
	3. resultado ← falso
	4. Si dx = 0,  y  Si dy = 0,  y  Si Recortar_Punto( P, R ) = verdadero, entonces
		5. Q ← P
		6. resultado ← verdadero
	7. Si no, entonces
		8. t_e ← 0
		9. t_s ← 1
		10. Si Calcular_Parámetros( R.x_izq-P.x, dx, t_e, t_s ) = verdadero, entonces
			11. Si Calcular_Parámetros( P.x-R.x_der, -dx, t_e, t_s ) = verdadero, entonces
				12. Si Calcular_Parámetros( R.y_inf-P.y, dy, t_e, t_s ) = verdadero, entonces
					13. Si Calcular_Parámetros( P.y-R.y_sup, -dy, t_e, t_s ) = verdadero, entonces
						14. resultado ← verdadero
						15. Si t_s < 1, entonces
							16. Q.x ← P.x + t_s dx
							17. Q.y ← P.y + t_s dy
						18. Si t_e > 0, entonces
							19. P.x ← P.x + t_e dx
							20. P.y ← P.y + t_e dy
	21. Terminar( resultado )

Si el segmento es aceptado, entonces el algoritmo terminará con el valor booleano verdadero. Además, los extremos, P y Q, contendrán los valores recortados por este mismo algoritmo. Si el segmento es rechazado, el algoritmo termina con el valor falso, lo cual implica que los parámetros, P y Q, no son alterados. En cualquier caso, se pasan estos dos parámetros por referencia, para así poder modificarlos.

A continuación presentamos el algoritmo para Calcular_Parámetros(), el cual requiere el numerador, el denominador, t_e, y t_s, los cuales estos dos últimos se pasan por referencia:

booleano Calcular_Parámetros( real numerador, real denominador, ref real t_e, ref real t_s )
	1. Si denominador > 0, entonces
		2. t ← numerador / denominador
		3. Si t > t_s
			4. Terminar( falso )
		5. Si no, compruebe que t > t_e
			6. t_e ← t
	7. Si no, compruebe que denominador < 0,
		8. t ← numerador / denominador
		9. Si t < t_e
			10. Terminar( falso )
		11. Si no, compruebe que t < t_s
			12. t_s ← t
	13. Si no, compruebe que numerador > 0,
		14. Terminar( falso )
	15. Terminar( verdadero )

Algoritmo de Nicholl-Lee-Nicholl

Este algoritmo intenta corregir los problemas de los algoritmos anteriores para recortar segmentos en un rectángulo vertical. El algoritmo de Cohen-Sutherland se basa en realizar varias comprobaciones, pero acaba calculando varias intersecciones que pueden o no servir. Los algoritmos de Cyrus-Beck y Liang-Barsky se basan en calcular varias intersecciones y luego comprobar cuáles sirven. El algoritmo de Nicholl-Lee-Nicholl elimina la necesidad de realizar todos estos cálculos de intersecciones favoreciendo las comprobaciones para dar con la intersección correcta, si existe. Al final, este algoritmo es más rápido que los mencionados anteriormente.

Para recortar un segmento con los extremos P y Q, necesitamos determinar las intersecciones, si existen, con las aristas. Comenzamos dividiendo la geometría en nueve regiones al extender horizontal y verticalmente las aristas del rectángulo vertical, como hicimos en el algoritmo de Cohen-Sutherland. Sin embargo, sólo necesitamos considerar tres casos de la posición del punto extremo, P, porque los demás casos son simétricos a uno de estos tres casos principales. Estos casos son:

P es interior al rectángulo de recorte,

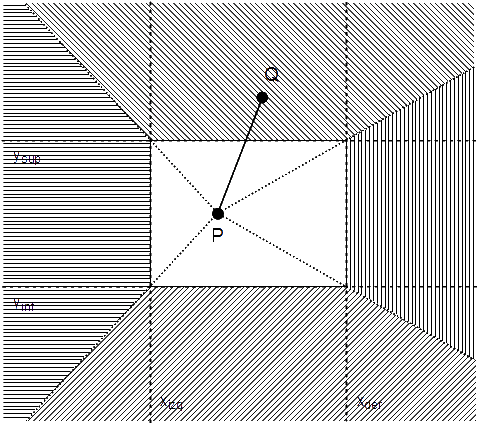
Figura 30 - Se divide el plano en varias regiones con el punto P interior
P está en una región exterior que hace esquina con el rectángulo de recorte, o

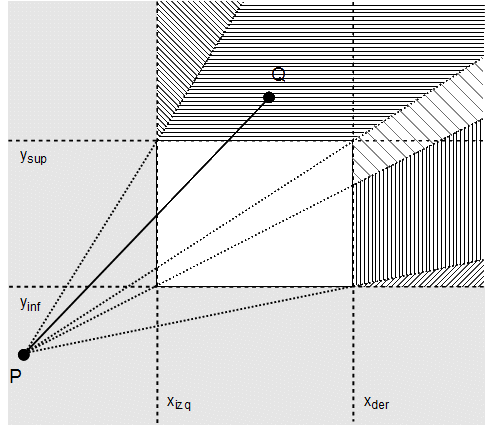
Figura 31 - Se divide el plano en varias regiones con el punto P en una esquina
P está en una región exterior que toca una arista del rectángulo de recorte.

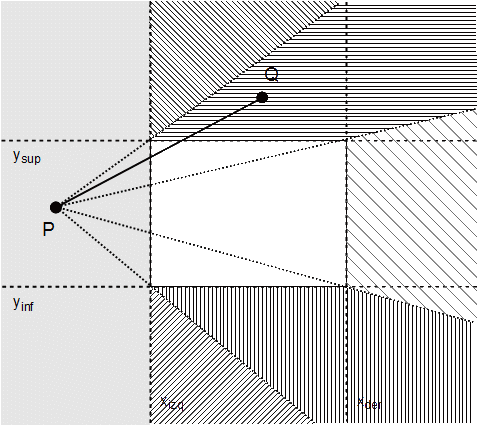
Figura 31 - Se divide el plano en varias regiones con el punto P en un lateral

En cada caso, podemos dividir nuevamente nuestro espacio en diferentes regiones para determinar dónde se encuentra el otro punto extremo, Q. Las nuevas divisiones se basan en crear vectores desde el punto conocido, P, a cada uno de los vértices del rectángulo de recorte. Al determinar si el punto extremo, Q, está a la izquierda de uno de estos vectores, de P a un vértice, podemos reducir las posibles regiones hasta encontrar la que contiene el punto, Q. Una vez que hayamos encontrado el punto, Q, y la región en la que se encuentra, podemos aplicar la ecuación de la intersección precisa para el caso en cuestión. Para los dos últimos casos, podemos pensar que los vectores de P a los vértices del rectángulo de recorte que son exteriores forman un "campo de visión". Cualquier punto dentro de este campo será visible y por tanto el segmento cruzará el rectángulo. Para el primer caso, usamos estos vectores simplemente para dividir el espacio en regiones para encontrar rápidamente el otro punto, Q, ya que sabemos de antemano que el segmento será visible, parcial o completamente.

Ejemplo

Descripción

A = ( -2, 1 )  y  B = ( 2, 2 )

Solución

Figura 34 - Calculamos el código regional del punto A como criterio del algoritmo a usar

Calculamos el código regional del punto A como hicimos en el método de Cohen-Sutherland:

A : 0001

Vemos que A está en una región lateral del rectángulo vertical de recorte. Esto significa que estamos ante el caso #2, en la figura 32.

Ahora nos toca descubrir la ubicación del punto B para determinar si hace falta recortar el segmento o no. Si es necesario recortar el segmento, debemos descubrir exactamente el punto de intersección. En principio, podemos comprobar si B está en alguna región vertical a la de A. Esto es,

B_x < R.x_izq  ⇒  2 < -1

Como no es cierto, debemos continuar con el algoritmo.

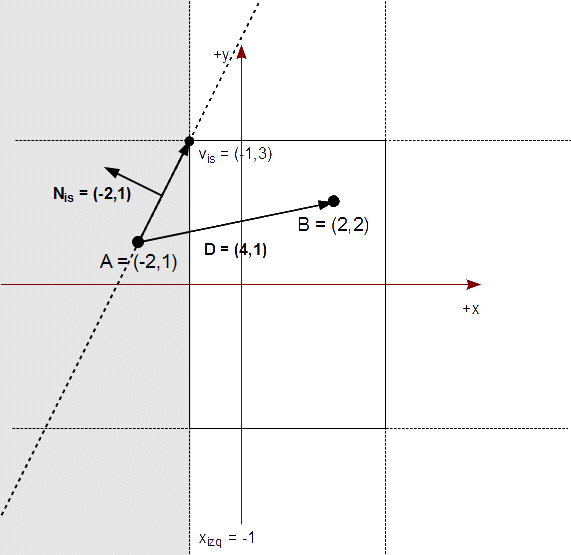
Figura 35 - Determinamos si B está a la izquierda o derecha de la línea AVis

Averiguamos si B está a la derecha o a la izquierda de una línea que contiene A y la esquina izquierda superior del rectángulo de recorte. Para ello, calculamos los siguientes vectores:

D = B - A = (  2,  2 ) - ( -2,  1 ) = (  4,  1 )
v_is = ( R.x_izq, R.y_sup ) - A = ( -1,  3 ) - ( -2,  1 ) = (  1,  2 )

Aplicamos el mismo método que usamos en el algoritmo de Cyrus-Beck para determinar si un punto estaba a un lado o a otro de una línea recta. Calculamos el vector normal de v_is - sin normalizar:

N_is = ( -2,  1 )

El signo de N ⋅ D nos indicará si B está a la izquierda o a la derecha:

( -2,  1 ) ⋅ (  4,  1 ) = (-2)*4 + 1*1 = -7 < 0

Como el signo es negativo, B está a la derecha y por tanto debemos continuar con el algoritmo.

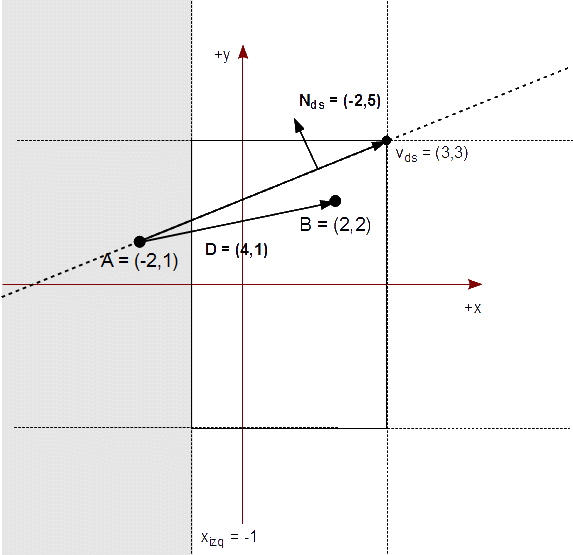
Figura 36 - Determinamos si B está a la izquierda o derecha de la línea AVds

Averiguamos si B está a la derecha o a la izquierda de una línea que contiene A y la esquina derecha superior del rectángulo de recorte. Para ello, calculamos el vector de tal línea:

v_ds = ( R.x_der, R.y_sup ) - A = (  3,  3 ) - ( -2,  1 ) = (  5,  2 )

Calculamos el vector normal de v_ds:

N_ds = ( -2,  5 )

El signo de N ⋅ D nos indicará si B está a la izquierda o a la derecha:

( -2,  5 ) ⋅ (  4,  1 ) = (-2)*4 + 5*1 = -3 < 0

Como el signo es negativo, B está a la derecha y por tanto debemos continuar con el algoritmo.

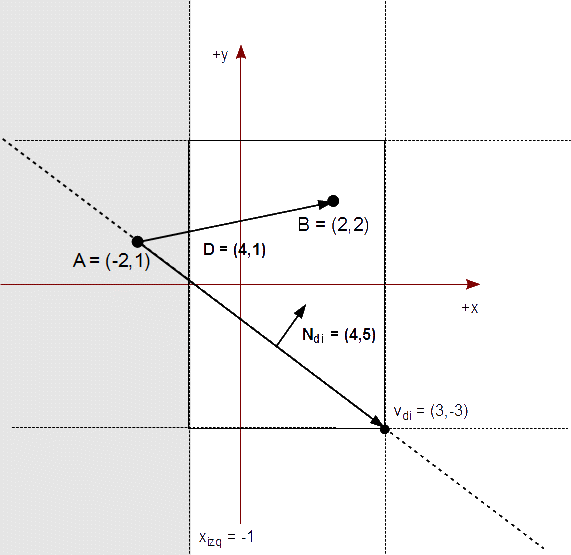
Figura 37 - Determinamos si B está a la izquierda o derecha de la línea AVdi

Averiguamos si B está a la derecha o a la izquierda de una línea que contiene A y la esquina derecha inferior del rectángulo de recorte. Para ello, calculamos el vector de tal línea:

v_di = ( R.x_der, R.y_inf ) - A = (  3, -3 ) - ( -2,  1 ) = (  5, -4 )

Calculamos el vector normal de v_di:

N_di = (  4,  5 )

El signo de N ⋅ D nos indicará si B está a la izquierda o a la derecha:

(  4,  5 ) ⋅ (  4,  1 ) = 4*4 + 5*1 = 21 > 0

Como el signo es positivo, B está a la izquierda de esta línea.

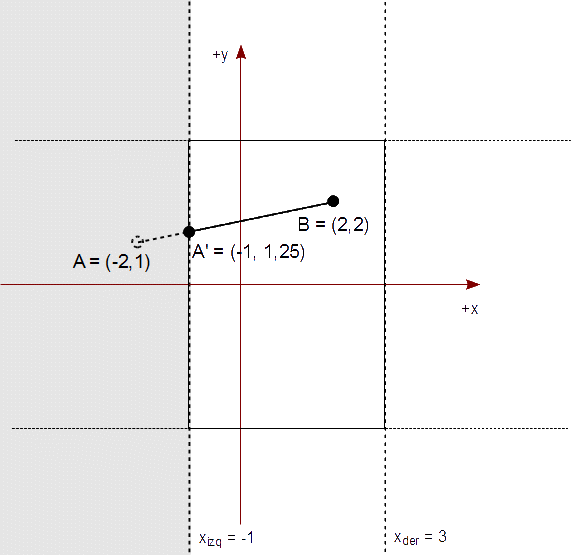
Figura 38 - Determinamos si B está a la izquierda o derecha de la arista derecha

Como B está a la izquierda de v_di pero a la derecha de v_ds, entonces sabemos que debemos recortar A con la arista izquierda:

A′_x = R.x_izq  ⇒  A′_x = -1
A′_y = A_y - (A_x - R.x_izq) * D_y / D_x
   = 1 - (-2 - (-1)) * 1 / 4  ⇒  A′_y = 1,25

B está o bien dentro del rectángulo de recorte o bien fuera. Esto implica que B está a la izquierda de la arista derecha del rectángulo, y por tanto es interior, o a la derecha, y por tanto se debe recortar. Realizamos una comprobación sencilla:

B_x < R.x_der  ⇒  2 < 3

Por lo tanto, B está dentro y no necesitamos realizar ninguna intersección. El segmento AB se recorta quedando como,

A′B = ( -1,  1,25 )

Algoritmo

La función principal es Recortar(), la cual aceptará tres parámetros: dos puntos extremos, P y Q, donde cada uno contiene las coordenadas (x,y) que representan el segmento a recortar, y un rectángulo vertical, R, que contiene los elementos {x_izq,y_sup, x_der,y_inf} representando las coordenadas de las dos esquinas izquierda superior y derecha inferior. Para hallar la región en la que se encuentra el punto extremo, P, del segmento a recortar, podemos usar el algoritmo de Calcular_Código() de Cohen-Sutherland para conseguir un código representativo de la región. Por ello, volvemos a definir los códigos binarios para: SUPERIOR=8, INFERIOR=4, DERECHA=2, e IZQUIERDA=1.

Como existen tres casos principales, definimos tres algoritmos especializados para recortar un segmento: Recortar_Interior(), Recortar_Izquierda_Inferior(), y Recortar_Izquierda(). Para los otros seis casos, modificamos los puntos extremos, P y Q, aplicando traslaciones y reflejo debido a las propiedades simétricas para convertir cada caso en uno principal. Cada algoritmo especializado hará uso de otros dos tipos de algoritmos:

La función Izquierda() nos indicará si un punto está a la izquierda (verdadero) de una línea representada por dos puntos o no (falso). La función Derecha() realizará una comprobación parecida si un punto está a la derecha (verdadero) de una línea o no (falso).
Las funciones Intersección_Vertical() e Intersección_Horizontal() calcularán la intersección entre el segmento, representado como un vector de A a B, y una arista vertical u horizontal del rectángulo de recorte, respectivamente.

booleano Recortar( ref Punto P, ref Punto Q, Rectángulo R )
	1. tipo ← Calcular_Código( P, R )
	2. Si no, compruebe que tipo = INTERIOR,      // Caso #1
		3. aceptar ← Recortar_Interior( P, Q, R )
	4. Si tipo = IZQUIERDA OR INFERIOR, entonces  // Caso #2
		5. aceptar ← Recortar_Izquierda_Inferior( P, Q, R )
	6. Si no, compruebe que tipo = DERECHA OR INFERIOR,
		7. T_x ← (R.x_izq + R.x_der) / 2
		8. P.x ← T_x - P.x
		9. Q.x ← T_x - Q.x
		10. aceptar ← Recortar_Izquierda_Inferior( P, Q, R )
		11. P.x ← T_x - P.x
		12. Q.x ← T_x - Q.x
	13.Si no, compruebe que tipo = IZQUIERDA OR SUPERIOR,
		14. T_y ← (R.y_sup + R.y_inf) / 2
		15. P.y ← T_y - P.y
		16. Q.y ← T_y - Q.y
		17. aceptar ← Recortar_Izquierda_Inferior( P, Q, R )
		18. P.y ← T_y - P.y
		19. Q.y ← T_y - Q.y
	20. Si no, compruebe que tipo = DERECHA OR SUPERIOR,
		21. T_x ← (R.x_izq + R.x_der) / 2
		22. T_y ← (R.y_sup + R.y_inf) / 2
		23. P ← T - P
		24. Q ← T - Q
		25. aceptar ← Recortar_Izquierda_Inferior( P, Q, R )
		26. P ← T - P
		27. Q ← T - Q
	28. Si no, compruebe que tipo = IZQUIERDA,     // Caso #3
		29. aceptar ← Recortar_Izquierda( P, Q, R )
	30. Si no, compruebe que tipo = DERECHA,
		31. T_x ← (R.x_izq + R.x_der) / 2
		32. P.x ← T_x - P.x
		33. Q.x ← T_x - Q.x
		34. aceptar ← Recortar_Izquierda( P, Q, R )
		35. P.x ← T_x - P.x
		36. Q.x ← T_x - Q.x
	37. Si no, compruebe que tipo = INFERIOR,
		38. T_x ← R.x_izq
		39. T_y ← R.y_inf
		40. P ← T - P
		41. Q ← T - Q
		42. aceptar ← Recortar_Izquierda( P, Q, R )
		43. P ← T - P
		44. Q ← T - Q
	45. Si no, compruebe que tipo = SUPERIOR,
		46. T_x ← R.x_izq
		47. T_y ← R.y_sup
		48. P ← T - P
		49. Q ← T - Q
		50. aceptar ← Recortar_Izquierda( P, Q, R )
		51. P ← T - P
		52. Q ← T - Q
	53. Terminar( aceptar )

Usamos el operador OR para indicar la operación OR a nivel de bits.

Aquí presentamos los algoritmos particulares para el recorte según la región donde se encuentra P, empezando por Recortar_Interior():

booleano Recortar_Interior( ref Punto P, ref Punto Q, Rectángulo R )
	1. aceptar ← verdadero
	2. PQ ← Q - P
	3. PVis ← (R.x_izq,R.y_sup) - P
	4. Si Izquierda( PQ, PVis ), entonces
		5. PVii ← (R.x_izq,R.y_inf) - P
		6. Si Izquierda( PQ, PVii ), entonces
			7. PVdi ← (R.x_der,R.y_inf) - P
			8. Si Izquierda( PQ, PVdi ), entonces
				9. Si Q.x > R.x_der, entonces
					10. Q ← Intersección_Vertical( P, Q, R.x_der )
			11. Si no, entonces
				12. Si Q.y < R.y_inf, entonces
					13. Q ← Intersección_Horizontal( P, Q, R.y_inf )
		14. Si no, entonces
			15. Si Q.x < R.x_izq, entonces
				16. Q ← Intersección_Vertical( P, Q, R.x_izq )
	17. Si no, entonces
		18. PVds ← (R.x_der,R.y_sup) - P
		19. Si Izquierda( PQ, PVds ), entonces
			20. Si Q.y > R.y_sup, entonces
				21. Q ← Intersección_Horizontal( P, Q, R.y_sup )
		22. Si no, entonces
			23. PVdi ← (R.x_der,R.y_inf) - P
			24. Si Izquierda( PQ, PVdi ), entonces
				25. Si Q.x > R.x_der, entonces
					26. Q ← Intersección_Vertical( P, Q, R.x_der )
			27. Si no, entonces
				28. Si Q.y < R.y_inf, entonces
					29. Q ← Intersección_Horizontal( P, Q, R.y_inf )
	30. Terminar( aceptar )

Aquí presentamos el algoritmo de Recortar_Izquierda_Inferior():

booleano Recortar_Izquierda_Inferior( ref Punto P, ref Punto Q, Rectángulo R )
	1. Si Q.x < R.x_izq, entonces
		2. aceptar ← falso
	3. Si no, compruebe que Q.y < R.y_inf,
		4. aceptar ← falso
	5. Si no, entonces
		6. PQ ← Q - P
		7. PVis ← (R.x_izq,R.y_sup) - P
		8. Si Izquierda( PQ, PVis ), entonces
			9. aceptar ← falso
		10. Si no, entonces
			11. PVds ← (R.x_der,R.y_sup) - P
			12. Si Izquierda( PQ, PVds ), entonces
				13. aceptar ← verdadero
				14. Si Q.y > R.y_sup, entonces
					15. Q ← Intersección_Horizontal( P, Q, R.y_sup )
				16. PVii ← (R.x_izq,R.y_inf) - P
				17. Si Izquierda( PQ, PVii ), entonces
					18. P ← Intersección_Vertical( P, Q, R.x_izq )
				19. Si no, entonces
					20. P ← Intersección_Horizontal( P, Q, R.y_inf )
			21. Si no, entonces
				22. PVdi ← (R.x_der,R.y_inf) - P
				23. Si Derecha( PQ, PVdi ), entonces
					24. aceptar ← falso
				25. Si no, entonces,
					26. aceptar ← verdadero
					27. Si Q.x > R.x_der, entonces
						28. Q ← Intersección_Vertical( P, Q, R.x_der )
					29. PVii ← (R.x_izq,R.y_inf) - P
					30. Si Izquierda( PQ, PVii ), entonces
						31. P ← Intersección_Vertical( P, Q, R.x_izq )
					32. Si no, entonces
						33. P ← Intersección_Horizontal( P, Q, R.y_inf )
	34.Terminar( aceptar )

Por último presentamos el algoritmo de Recortar_Izquierda():

booleano Recortar_Izquierda( ref Punto P, ref Punto Q, Rectángulo R )
	1. Si Q.x < R.x_izq, entonces
		2. aceptar ← falso
	3. Si no, entonces
		4. PQ ← Q - P
		5. PVis ← (R.x_izq,R.y_sup) - P
		6. Si Izquierda( PQ, PVis ), entonces
			7. aceptar ← falso
		8. Si no, entonces
			9. PVds ← (R.x_der,R.y_sup) - P
			10. Si Izquierda( PQ, PVds ), entonces
				11. aceptar ← verdadero
				12. P ← Intersección_Vertical( P, Q, R.x_izq )
				13. Si Q.y > R.y_sup, entonces
					14. Q ← Intersección_Horizontal( P, Q, R.y_sup )
			15. Si no, entonces
				16. PVdi ← (R.x_der,R.y_inf) - P
				17. Si Izquierda( PQ, PVdi ), entonces
					18. aceptar ← verdadero
					19. P ← Intersección_Vertical( P, Q, R.x_izq )
					20. Si Q.x > R.x_der, entonces
						21. Q ← Intersección_Vertical( P, Q, R.x_der )
				22. Si no, entonces
					23. PVii ← (R.x_izq,R.y_inf) - P
					24. Si Derecha( PQ, PVii ), entonces
						25. aceptar ← falso
					26. Si no, entonces
						27. aceptar ← verdadero
					28. P ← Intersección_Vertical( P, Q, R.x_izq )
					29. Si Q.y < R.y_inf, entonces
						30. Q ← Intersección_Horizontal( P, Q, R.y_inf )
	31. Terminar( aceptar )

Estos cuatro algoritmos son auxiliares para los algoritmos de recorte.

booleano Izquierda( Vector A, Vector B )
	1. Si -B.y * A.x + B.x * A.y > 0, entonces
		2. Terminar( verdadero )
	3. Si no, entonces
		4. Terminar( falso )

booleano Derecha( Vector A, Vector B )
	1. Si -B.y * A.x + B.x * A.y < 0, entonces
		2. Terminar( verdadero )
	3. Si no, entonces
		4. Terminar( falso )

Podemos implementar este algoritmo como un caso especial de Izquierda(). Esto es,

booleano Derecha( Vector A, Vector B )
	1. Terminar( Izquierda( -A, B ) )

Por lo tanto, podríamos prescindir del uso de este algoritmo, Derecha().

Punto Intersección_Vertical( Punto A, Punto B, real Arista )
	1. D ← B.x - A.x
	2. Si D = 0, entonces
		3. Resultado.x ← Arista
		4. Resultado.y ← A.y
	5. Si no, entonces
		6. Resultado.x ← Arista
		7. Resultado.y ← A.y - (B.y - A.y) * (A.x - Arista) / D
	8. Terminar( Resultado )

Punto Intersección_Horizontal( Punto A, Punto B, real Arista )
	1. D ← B.y - A.y
	2. Si D = 0, entonces
		3. Resultado.x ← A.x
		4. Resultado.y ← Arista
	5. Si no, entonces
		6. Resultado.x ← A.x - (B.x - A.x) * (A.y - Arista) / D
		7. Resultado.y ← Arista
	8. Terminar( Resultado )

Algoritmo de Sutherland-Hodgman

Este algoritmo se basa en recortar el polígono parcialmente usando cada lado del rectángulo vertical de recorte hasta terminar con la intersección final, interior al rectángulo. El polígono a recortar se representa como una lista de vértices: v₁,v₂,v₃,...,v_n. Nos interesa que esta lista de vértices esté ordenada para que cada pareja contigua de vértices represente una arista del polígono. Esto significa que ordenaremos la lista geométricamente en el sentido de las agujas del reloj o en el sentido contrario, según elijamos. Los vértices v_i y v_i+1 describen una arista del polígono, hasta llegar a v_n que forma la última arista con el vértice, v₁. Cada recorte del polígono generará una nueva lista de vértices que representará el nuevo polígono resultante del recorte.

Para cada recorte por el lado del rectángulo, existen cuatro casos a comprobar para cada pareja de vértices que representa una arista del polígono a recortar. Según las regiones formadas por cada lado de recorte, los vértices se encontrarán dentro o fuera de ellas, éstos son:

Si ambos vértices están dentro, entonces sólo agregamos el segundo vértice a la lista resultante de vértices.

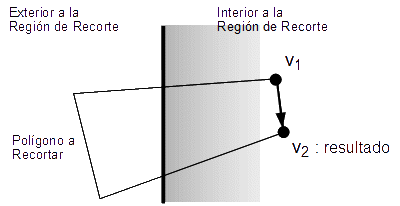
Figura 39 - Ambos vértices están dentro
Si el primer vértice está dentro de la arista, pero el segundo está fuera, entonces calculamos el punto de intersección. Sólo agregamos este punto de intersección a la lista resultante de vértices.

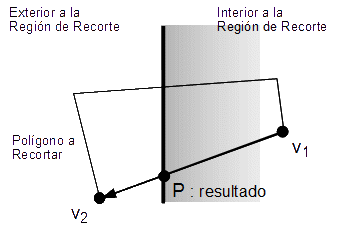
Figura 40 - El primer vértice está dentro, pero el segundo está fuera
Si el primer vértice está fuera de la arista, pero el segundo está dentro, entonces tenemos que calcular el punto de intersección. Este punto de intersección y el segundo vértice son agregados a la lista resultante de vértices.

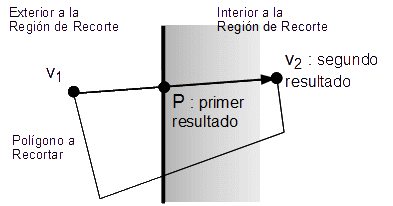
Figura 41 - El primer vértice está fuera, pero el segundo está dentro
Si ambos vértices están fuera, entonces no modificamos la lista resultante de vértices.

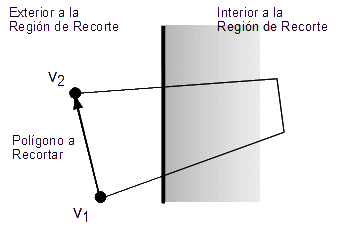
Figura 42 - Ambos vértices están fuera

Pasamos la lista resultante de vértices como la lista entrante al mismo algoritmo para las demás aristas del rectángulo.

Ejemplo

Descripción

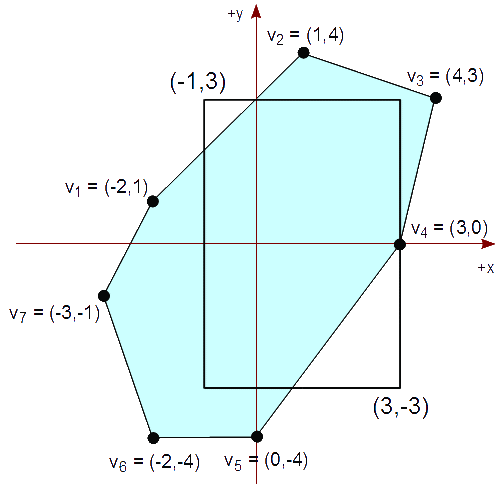
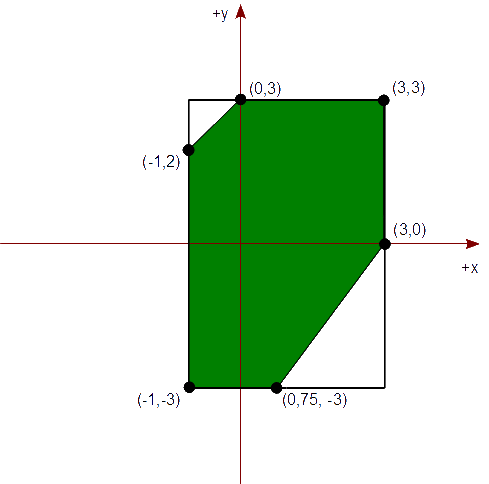
Tenemos un rectángulo vertical de recorte cuya diagonal es de (-1,3) a (3,-3) que representa nuestra vista. Queremos un polígono (convexo), en tal rectángulo de recorte, descrito por la siguiente lista de vértices:

{ (-2,1), (1,4), (4,3), (3,0), (0,-4), (-2,-4), (-3,-1) }

Solución

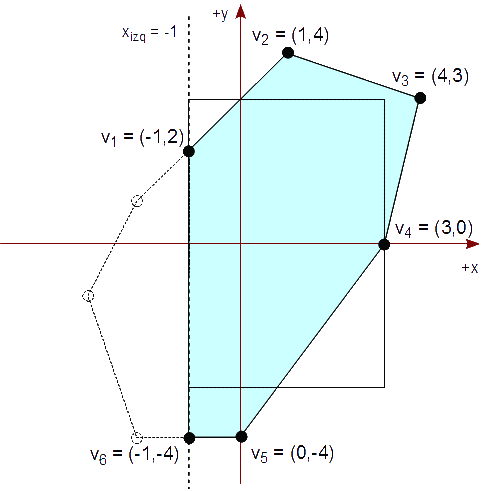
Figura 44 - Recortamos el polígono con el lado izquierdo del rectángulo de recorte

Empezamos el recorte de nuestro polígono con el lado izquierdo de nuestro rectángulo vertical de recorte que es x_izq = -1. Elegimos cada arista de nuestro polígono y la comprobamos según su caso, mencionado previamente. También creamos una lista de vértices para representar el polígono resultante del recorte.

Vemos que de v₁ a v₂, se nos presenta el caso #3, ya que v₁ está fuera del lado del rectángulo y v₂ está dentro. Por lo tanto, calculamos el punto de intersección del segmento con x_izq = -1,

P_x = x_izq = -1
                   v_{2_y} - v_{1_y}
P_y = v_{2_y} + (x_izq - v_{2_x}) * ----------
                   v_{2_x} - v_{1_x}
  = 4 + (-1 - 1) * 3 / 3 = 2

Agregamos este punto de intersección y el vértice v₂ a la lista resultante de vértices, en este orden. La lista resultante es ahora:

{ (-1,2), (1,4) }

Comprobamos el segmento de v₂ a v₃. Como ambos son interiores al lado izquierdo del rectángulo de recorte, estamos ante el caso #1, por lo que agregamos v₃ a la lista resultante. La lista resultante es ahora:

{ (-1,2), (1,4), (4,3) }

Comprobamos el segmento de v₃ a v₄. Como ambos son interiores al lado izquierdo del rectángulo de recorte, estamos ante el caso #1, por lo que agregamos v₄ a la lista resultante. La lista resultante es ahora:

{ (-1,2), (1,4), (4,3), (3,0) }

Comprobamos el segmento de v₄ a v₅. Como ambos son interiores al lado izquierdo del rectángulo de recorte, estamos ante el caso #1, por lo que agregamos v₅ a la lista resultante. La lista resultante es ahora:

{ (-1,2), (1,4), (4,3), (3,0), (0,-4) }

Vemos que el segmento de v₅ a v₆ trata del caso #2. Por lo tanto, calculamos el punto de intersección del segmento con x_izq = -1,

P_x = x_izq = -1
                   v_{6_y} - v_{5_y}
P_y = v_{6_y} + (x_izq - v_{6_x}) * ----------
                   v_{6_x} - v_{5_x}
  = -4 + (-1 - (-2)) * 0 / 2 = -4

Agregamos este punto de intersección a la lista resultante de vértices. La lista resultante es ahora:

{ (-1,2), (1,4), (4,3), (3,0), (0,-4), (-1,-4) }

Comprobando los dos últimos segmentos, v₆ a v₇ y v₇ a v₁, vemos que están fuera. Por lo tanto, no agregamos ningún vértice a la lista resultante. Al final, la lista resultante es:

{ (-1,2), (1,4), (4,3), (3,0), (0,-4), (-1,-4) }

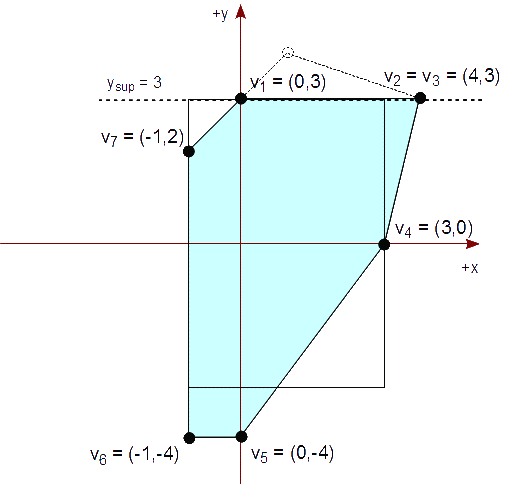
Figura 45 - Recortamos el polígono con el lado superior del rectángulo de recorte

Continuamos el recorte con el lado superior de nuestro rectángulo vertical de recorte que es y_sup = 3. Elegimos cada arista de nuestro polígono actual, previamente recortado, y la comprobamos según su caso, mencionado previamente.

Vemos que de v₁ a v₂, se nos presenta el caso #2, ya que v₁ está dentro del lado del rectángulo y v₂ está fuera. Por lo tanto, calculamos el punto de intersección del segmento con y _sup = 3,

                   v_{2_x} - v_{1_x}
P_x = v_{2_x} + (y_sup - v_{2_y}) * ----------
                   v_{2_y} - v_{1_y}
  = 1 + (3 - 4) * 2 / 2 = 0
P_y = y_sup = 3

Agregamos este punto de intersección a la lista resultante de vértices. La lista resultante es ahora:

{ (0,3) }

Comprobamos que el segmento de v₂ a v₃ presenta el caso #3, ya que v₂ está fuera del lado del rectángulo y v₃ está (justo) dentro. Por lo tanto, calculamos el punto de intersección del segmento con y_sup = 3,

                   v_{3_x} - v_{2_x}
P_x = v_{3_x} + (y_sup - v_{3_y}) * ----------
                   v_{3_y} - v_{2_y}
  = 4 + (3 - 3) * 3 / (-1) = 4
P_y = y_sup = 3

Agregamos este punto de intersección y el vértice v₃ a la lista resultante de vértices, en este orden. La lista resultante es ahora:

{ (0,3), (4,3), (4,3) }

Comprobando el resto de los segmentos vemos que están dentro del semiplano, y_sup = 3. Por lo tanto, agregamos los segundos vértices de cada segmento a la lista resultante. Al final, la lista resultante es:

{ (0,3), (4,3), (4,3), (3,0), (0,-4), (-1,-4), (-1,2) }

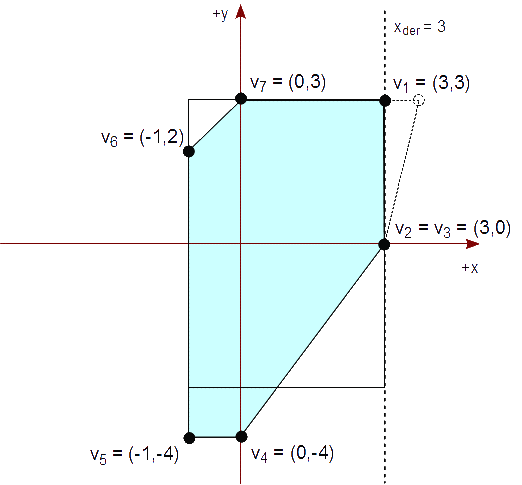
Figura 46 - Recortamos el polígono con el lado derecho del rectángulo de recorte

Continuamos el recorte con el lado derecho de nuestro rectángulo vertical de recorte que es x_der = 3. Elegimos cada arista de nuestro polígono actual, previamente recortado, y la comprobamos según su caso, mencionado previamente.

Vemos que de v₁ a v₂, se nos presenta el caso #2, ya que v₁ está dentro del lado del rectángulo y sub>2 está fuera. Por lo tanto, calculamos el punto de intersección del segmento con x_der = 3,

P_x = x_der = 3
                   v_{2_y} - v_{1_y}
P_y = v_{2_y} + (x_der - v_{2_x}) * ----------
                   v_{2_x} - v_{1_x}
  = 3 + (3 - 4) * 0 / 4 = 3

Agregamos este punto de intersección a la lista resultante de vértices. La lista resultante es ahora:

{ (3,3) }

Como el "segmento" de v₂ a v₃ está fuera del semiplano, x_der = 3, no agregamos ninguno de los dos vértices. La lista resultante sigue siendo:

{ (3,3) }

Comprobamos que el segmento de v₃ a v₄ presenta el caso #3, ya que v₃ está fuera del lado del rectángulo y v₄ está (justo) dentro. Por lo tanto, calculamos el punto de intersección del segmento con x_der = 3,

P_x = x_der = 3
                   v_{4_y} - v_{3_y}
P_y = v_{4_y} + (x_der - v_{4_x}) * ----------
                   v_{4_x} - v_{3_x}
  = 0 + (3 - 3) * (-3) / (-1) = 0

Agregamos este punto de intersección y el vértice v₃ a la lista resultante de vértices, en este orden. La lista resultante es ahora:

{ (3,3), (3,0), (3,0) }

Comprobando el resto de los segmentos vemos que están dentro del semiplano, x_der = 3. Por lo tanto, agregamos los segundos vértices de cada segmento a la lista resultante. Al final, la lista resultante es:

{ (3,3), (3,0), (3,0), (0,-4), (-1,-4), (-1,2), (0,3) }

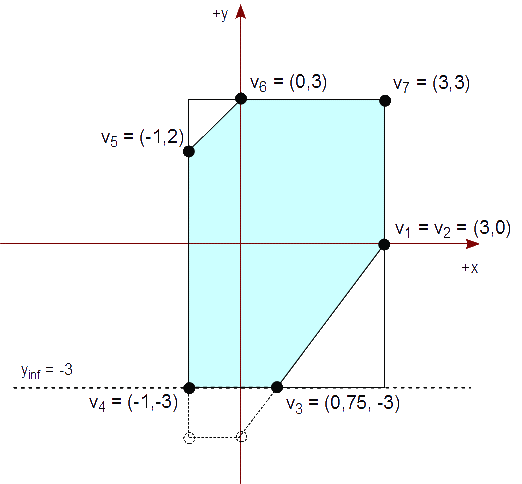
Figura 47 - Recortamos el polígono con el lado inferior del rectángulo de recorte

Continuamos el recorte con el lado inferior de nuestro rectángulo vertical de recorte que es y_inf = -3. Elegimos cada arista de nuestro polígono actual, previamente recortado, y la comprobamos según su caso, mencionado previamente.

Comprobamos que tanto el segmento de v₁ a v₂ como el "segmento" de v₂ a v₃ están dentro del semiplano, y_inf = -3. Por lo tanto, agregamos los segundos vértices de cada segmento a la lista resultante. Al final, la lista resultante es:

{ (3,0), (3,0) }

Vemos que de v₃ a v₄, se nos presenta el caso #2, ya que v₃ está dentro del lado del rectángulo y v₄ está fuera. Por lo tanto, calculamos el punto de intersección del segmento con y_inf = -3,

                   v_{4_x} - v_{3_x}
P_x = v_{4_x} + (y_inf - v_{4_y}) * ----------
                   v_{4_y} - v_{3_y}
  = 0 + (-3 - (-4)) * (-3) / (-4) = 0,75
P_y = y_inf = -3

Agregamos este punto de intersección a la lista resultante de vértices. La lista resultante es ahora:

{ (3,0), (3,0), (0,75, -3) }

Como el segmento de v₄ a v₅ está fuera del semiplano, y_inf = -3, no agregamos ninguno de los dos vértices. La lista resultante sigue siendo:

{ (3,0), (3,0), (0,75, -3) }

Comprobamos que el segmento de v₅ a v₆ presenta el caso #3, ya que v₅ está fuera del lado del rectángulo y v₆ está dentro. Por lo tanto, calculamos el punto de intersección del segmento con y_inf = -3,

                   v_{6_x} - v_{5_x}
P_x = v_{6_x} + (y_inf - v_{6_y}) * ----------
                   v_{6_y} - v_{5_y}
  = -1 + (-3 - 2) * 0 / 6 = -1
P_y = y_inf = -3

Agregamos este punto de intersección y el segundo vértice, v₆, a la lista resultante de vértices. La lista resultante es ahora:

{ (3,0), (3,0), (0,75, -3), (-1,-3), (-1,2) }

Comprobando el resto de los segmentos vemos que están dentro del semiplano, y_inf = -3. Por lo tanto, agregamos los segundos vértices de cada segmento a la lista resultante. Al final, la lista resultante es:

{ (3,0), (3,0), (0,75, -3), (-1,-3), (-1,2), (0,3), (3,3) }

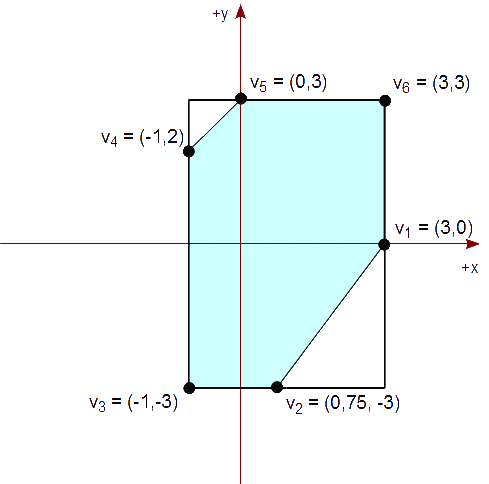
Figura 48 - El polígono resultante sin vértices contiguos repetidos

Vemos que el polígono final contiene vértices contiguos repetidos, por lo que podemos procesar nuestra lista de vértices para eliminar las repeticiones. Al final, nos queda la siguiente lista de vértices:

{ (3,0), (0,75, -3), (-1,-3), (-1,2), (0,3), (3,3) }

Algoritmo

El algoritmo se basa en el pseudo-código principal, Recortar(). Tenemos otros algoritmos auxiliares:

Recortar_Lado() sirve para recortar un segmento descrito por dos vértices por un lado particular del rectángulo de recorte. También se requiere la lista resultante de vértices para poder agregar nuevos vértices a ella. La salida es la misma lista resultante actualizada de los vértices del polígono recortado.
Interior() indica si un punto se considera candidato como interior (verdadero) al rectángulo de recorte o se acepta como exterior (falso).
Intersectar() calcula el punto de intersección entre un segmento y un lado dado del rectángulo de recorte.

Presentamos el algoritmo para Recortar():

Polígono Recortar( Polígono P, Rectángulo R )
	1. Resultado, Actual : Polígono
	2. Actual ← P
	3. Para cada lado de R, repetir
		4. Resultado ← vacío  // Resultado es un polígono vacío
		5. Para: i ← 1 hasta n, repetir
			6. Resultado ← Recortar_Lado( Actual.v_i, Actual.v_i+1, lado, R, Resultado )
		7. Resultado ← Recortar_Lado( Actual.v_n, Actual.v₁, lado, R, Resultado )  // Recortamos la última arista de Actual: v_nv₁
		8. Actual ← Resultado
	9. Resultado ← Eliminar_Repeticiones( Resultado )
	10. Terminar( Resultado )

Eliminar_Repeticiones() recorre la lista dada de vértices del polígono para eliminar repeticiones contiguas. También hay que comprobar el último vértice con el primero, ya que forman un segmento.

He aquí el algoritmo de Recortar_Lado() que modifica el polígono, Resultado, y lo regresa al terminar:

Polígono Recortar_Lado( Punto v1, Punto v2, Lado L, Rectángulo R, ref Polígono Resultado )
	1. interior1 ← Interior( v1, L, R )
	2. interior2 ← Interior( v2, L, R )
	3. Si interior1 = verdadero, entonces
		4. Si interior2 = verdadero, entonces
			5. Resultado.Agregar( v2 )
		6. Si no, entonces,
			7. P ← Intersectar( v1, v2, L, R )
			8. Resultado.Agregar( P )
	9. Si no, compruebe que  interior2 = verdadero,
		10. P ← Intersectar( v1, v2, L, R )
		11. Resultado.Agregar( P )
		12. Resultado.Agregar( v2 )
	13. Terminar( Resultado )

Agregar() se refiere a la operación básica para agregar un punto a la lista de vértices de un polígono.

Exponemos la lógica de Interior():

booleano Interior( Punto v, Lado L, Rectángulo R )
	1. Si L = Izquierdo, entonces
		2. Si v_x ≥ R.x_izq, entonces
			3. bEsInterior ← verdadero
		4. Si no, entonces
			5. bEsInterior ← falso
	6. Si no, compruebe que  L = Superior, entonces
		7. Si v_y ≤ R.y_sup, entonces
			8. bEsInterior ← verdadero
		9. Si no, entonces
			10. bEsInterior ← falso
	11. Si no, compruebe que  L = Derecho, entonces
		12. Si v_x ≤ R.x_der, entonces
			13. bEsInterior ← verdadero
		14. Si no, entonces
			15. bEsInterior ← falso
	16. Si no, compruebe que  L = Inferior, entonces
		17. Si v_y ≥ R.y_inf, entonces
			18. bEsInterior ← verdadero
		19. Si no, entonces
			20. bEsInterior ← falso
	21. Terminar( bEsInterior )

Este algoritmo para Intersectar() involucra un rectángulo vertical de recorte:

Punto Intersectar( Punto v1, Punto v2, Lado L, Rectángulo R )
	1. dx ← v2.x - v1.x
	2. dy ← v2.y - v1.y
	3. Si L = Izquierdo, entonces
		4. P.x ← R.x_izq
		5. Si dx ≠ 0, entonces
			6. P.y ← v2.y + (R.x_izq - v2.x) * dy / dx
		7. Si no, entonces
			8. P.y ← v2.y
	9. Si no, compruebe que  L = Superior, entonces
		10. Si dy ≠ 0, entonces
			11. P.x ← v2.x + (R.y_sup - v2.y) * dx / dy
		12. Si no, entonces
			13. P.x ← v2.x
		14. P.y ← R.y_sup
	15. Si no, compruebe que  L = Derecho, entonces
		16. P.x ← R.x_der
		17. Si dx ≠ 0, entonces
			18. P.y ← v2.y + (R.x_der - v2.x) * dy / dx
		19. Si no, entonces
			20. P.y ← v2.y
	21. Si no, compruebe que  L = Inferior, entonces
		22. Si dy ≠ 0, entonces
			23. P.x ← v2.x + (R.y_inf - v2.y) * dx / dy
		24. Si no, entonces
			25. P.x ← v2.x
		26. P.y ← R.y_inf
	27. Terminar( P )

Algoritmo de Liang-Barsky

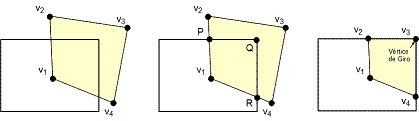
Figura 49 - Se agrega el vértice de giro, que es un vértice del rectángulo de recorte

El algoritmo de Liang-Barsky para recortar líneas puede ser ampliado para recortar polígonos en un rectángulo vertical. La idea principal de este algoritmo se basa en la detección de vértices de giro. Un vértice de giro es aquel vértice de la esquina del rectángulo de recorte que formará parte del polígono recortado. Esta posibilidad existe si una arista del polígono a recortar cruza un lado del rectángulo de recorte seguida de una o más aristas que giran entorno a la esquina del rectángulo de recorte, para volver a cruzar el rectángulo por otro lado. Si esto ocurriere, entonces agregaríamos este vértice de giro a nuestra lista de vértices resultante que representa el polígono recortado.

Fijémonos en varios casos de intersección de líneas rectas diagonales - aquéllas que no son verticales ni horizontales. Extendemos las aristas del rectángulo vertical para que sean líneas y así creamos nueve regiones: ocho externas y una interna. Esto implica que una línea diagonal cruza de una esquina regional a otra esquina opuesta.

Si parte de un segmento del polígono yace dentro del rectángulo de recorte, entonces esa parte debe pertenecer al polígono resultante. Debemos agregar los vértices de este segmento, dependiendo de las circunstancias:

El segmento yace completamente en el interior del rectángulo de recorte, por lo que ambos extremos del segmento son agregados a la lista de vértices del polígono resultante.
El segmento yace parcialmente en el interior, con un extremo dentro del rectángulo de recorte. Esto implica que hay que calcular el punto de intersección con un lado del rectángulo. Se agrega el extremo interior del segmento y el punto de intersección a la lista de vértices del polígono resultante.
El segmento yace parcialmente en el interior, pero ambos puntos extremos yacen fuera del rectángulo de recorte. Esto supone calcular dos puntos de intersección con dos lados diferentes del rectángulo. Ambos puntos de intersección son agregados a la lista de vértices del polígono resultante.

Por otro lado, podemos tener el caso de que el segmento no cruce el interior del rectángulo de recorte, pero el siguiente segmento que representa una arista del polígono sí puede cruzar el rectángulo. Como nos limitamos a mirar cada arista según su primer vértice, podemos determinar el lado del rectángulo, si se empieza en una región adyacente a un lado, que el segmento puede cruzar, o entre dos lados, si se empieza en una esquina.

Volviendo al tema del vértice de giro, agregamos tal vértice a la lista de vértices resultante, cuando una arista entra una esquina.

El algoritmo original propuesto por Liang y Barsky funciona de otra manera. Se agrega el vértice de giro a la lista resultante cuando una arista abandona la esquina. Sin embargo, esto no elimina el problema de la arista degenerada y además complica la lectura del algoritmo más de la cuenta. Por lo tanto, usaremos nuestra versión del algoritmo.

Basándonos en la solución dada por Liang y Barsky para recortar segmentos, haremos uso de la ecuación paramétrica de una línea recta y analizaremos los cuatro valores del parámetro, t, debidos a las cuatro intersecciones de la línea, que contiene la arista, con las líneas formadas por las extensiones de los lados del rectángulo de recorte. Dos valores son considerados potencialmente entrantes: t_e₁ y t_e₂ y los otros dos son considerados potencialmente salientes: t_s₁ y t_s₂. Tomemos nota de que t_e₁ es el menor y t_s₂ es el mayor de los cuatro valores calculados; los otros dos valores pueden estar en cualquier orden. Como explicamos en el apartado del algoritmo de Liang-Barsky para recortar segmentos, si t_e₂ ≤ t_s₁, entonces la línea cruza el rectángulo de recorte; si t_e₂ > t_s₁, entonces la línea pasa de una esquina a otra.

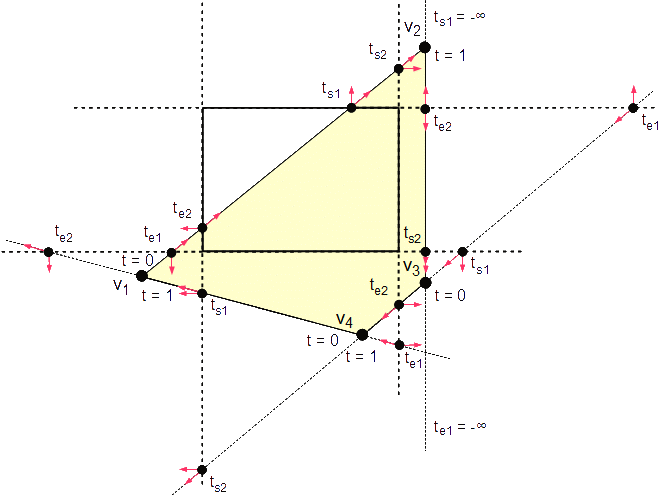
Figura 50 - Diferentes casos de los cuatro parámetros de puntos de intersección

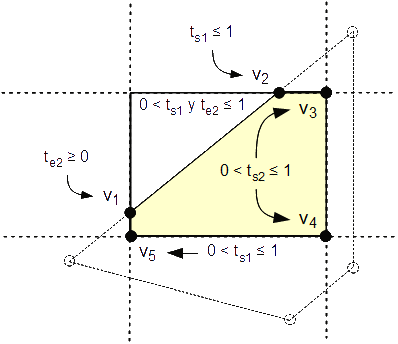
Como ya sabemos, los valores de t deben estar comprendidos entre 0 y 1 para representar el segmento, donde t=0 implica un punto extremo y t=1 se refiere al otro. Estableciendo la relación entre estos valores paramétricos y los cuatro valores de las intersecciones, podemos determinar la contribución de la arista al polígono recortado resultante. Si 0 < t_s₁ y t_e₂ ≤ 1, entonces la arista comienza o incluso puede terminar dentro del rectángulo. Como existe una parte visible de esta arista, debemos agregarla a nuestro polígono recortado.

Si la arista no cruza el rectángulo de recorte, entonces la línea, donde yace la arista, atraviesa tres esquinas: dos opuestas entre sí y una en el medio. Si la arista yace en cualquiera de estas dos esquinas opuestas, entonces se debe agregar un vértice de giro a la lista de vértices resultante. Entrada a esta esquina del medio, se comprueba con 0 < t_s₁ ≤ 1. Entrando la última esquina se comprueba con 0 < t_s₂ ≤ 1, que también es válida para el caso de que la arista cruce el rectángulo de recorte, y por tanto se debe agregar el vértice de giro.

El problema del algoritmo es que tenemos que tratar los casos especiales cuando las aristas son horizontales o verticales. Una solución es considerar cada caso cuando se presente, aplicando otra lógica especial que requiere un análisis para cada caso. La otra solución es describir estas aristas de tal manera que podamos usar la misma lógica del algoritmo para todas las aristas. Para implementar esta solución, asignamos los valores de +∞ y -∞ para los parámetros entrantes y salientes.

Figura 51 - Polígono recortado junto con las condiciones satisfechas

Ejemplo

Descripción

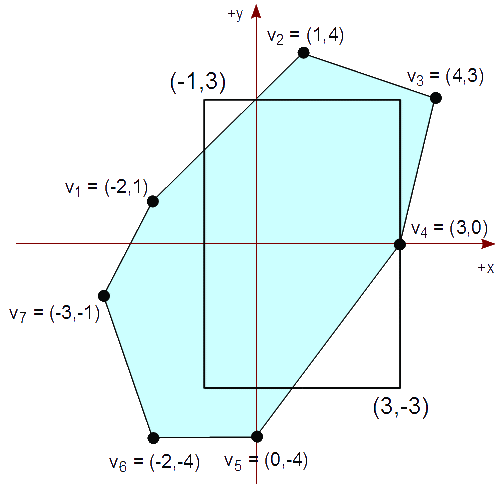
Retomamos el mismo ejemplo anterior del método de Sutherland-Hodgman. Tenemos un rectángulo vertical de recorte cuya diagonal es de (-1,3) a (3,-3) que representa nuestra vista. Queremos un polígono, en tal rectángulo de recorte, a partir del polígono, P, descrito por la siguiente lista de vértices:

P : { (-2,1), (1,4), (4,3), (3,0), (0,-4), (-2,-4), (-3,-1) }

Solución

Figura 53 - Analizamos la primera arista del polígono

Creamos una lista de vértices, Q, para representar el polígono resultante del recorte, inicialmente vacía:

Q : {}

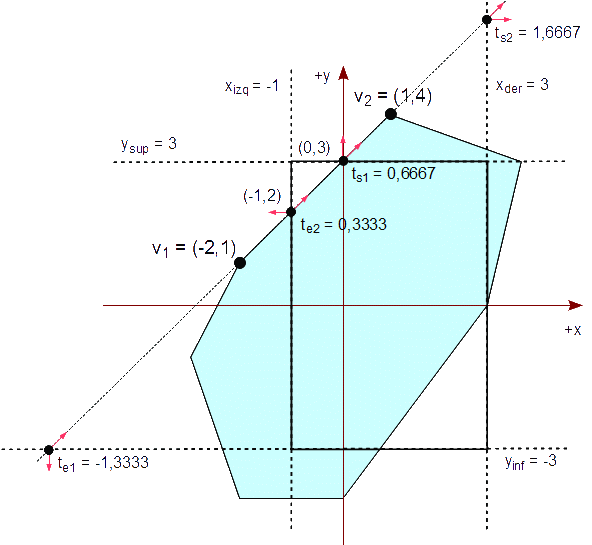
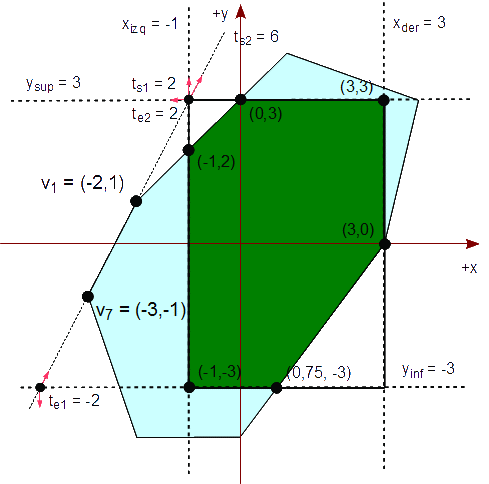
Empezamos el recorte de nuestro polígono analizando el primer segmento formado por v₁v₂. Calculamos las cuatro intersecciones y las clasificamos a través de sus parámetros.

Δ_x = v_{2_x} - v_{1_x} = 1 - (-2) = 3
Δ_y = v_{2_y} - v_{1_y} = 4 - 1 = 3

t_e₁ =  (v_{1_y} - y_inf) / -Δ_y =  ( 1 - (-3) ) / (-3) = -1,3333
t_e₂ = -(v_{1_x} - x_izq) /  Δ_x = -( (-2) - (-1) ) / 3 =  0,3333
t_s₁ = -(v_{1_y} - y_sup) /  Δ_y = -( 1 - 3 ) / 3       =  0,6667
t_s₂ =  (v_{1_x} - x_der) / -Δ_x =  ( (-2) - 3 ) / (-3) =  1,6667

Como t_s₂ > 0, t_e₂ ≤ t_s₁, 0 < t_s₁ y t_e₂ ≤ 1, el segmento es completa o parcialmente visible en el rectángulo de recorte. Como t_e₂ > 0, calculamos el punto de intersección

(x,y) = v₁ + t_e₂ * (Δ_x,Δ_y) = (-2,1) + 0,3333 * (3,3)
      = (-1,2)

y lo agregamos a la lista resultante, Q. La lista resultante es ahora:

Q : { (-1,2) }

Como t_s₁ < 1, calculamos el punto de intersección

(x,y) = v_{1_x} + t_s₁ * (Δ_x,Δ_y) = (-2,1) + 0,6667 * (3,3)
      = (0,3)

y lo agregamos a la lista resultante, Q. La lista resultante es ahora:

Q : { (-1,2), (0,3) }

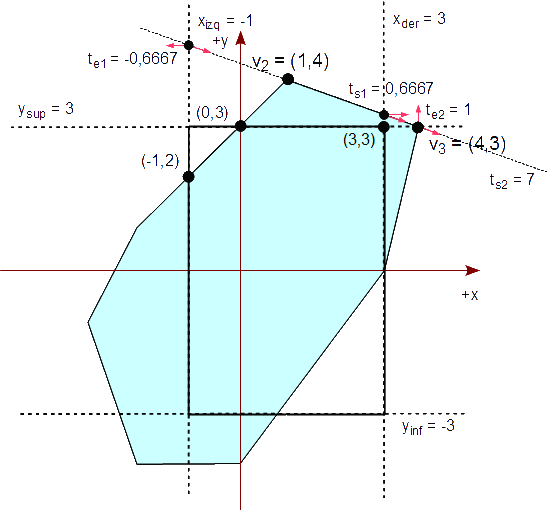
Figura 54 - Analizamos la segunda arista del polígono

Seguimos con el análisis con el segundo segmento formado por v₂v₃. Calculamos las cuatro intersecciones y las clasificamos a través de sus parámetros.

Δ_x = v_{3_x} - v_{2_x} = 4 - 1 = 3
Δ_y = v_{3_y} - v_{2_y} = 3 - 4 = -1

t_e₁ = -(v_{2_x} - x_izq) /  Δ_x = -( 1 - (-1) ) / 3     = -0,6667
t_e₂ = -(v_{2_y} - y_sup) /  Δ_y = -( 4 - 3 ) / (-1)     =  1
t_s₁ =  (v_{2_x} - x_der) / -Δ_x =  ( 1 - 3 ) / (-3)     =  0,6667
t_s₂ =  (v_{2_y} - y_inf) / -Δ_y =  ( 4 - (-3) ) / -(-1) =  7

Aunque t_s₂ > 0, t_e₂ > t_s₁, el segmento no es visible en el rectángulo de recorte. Sin embargo, como 0 < t_s₁ ≤ 1, agregamos el vértice de giro: (3,3) a la lista resultante, Q. La lista resultante es ahora:

Q : { (-1,2), (3,3) }

Como t_s₂ > 1, no agregamos el otro vértice de giro: (3,-3).

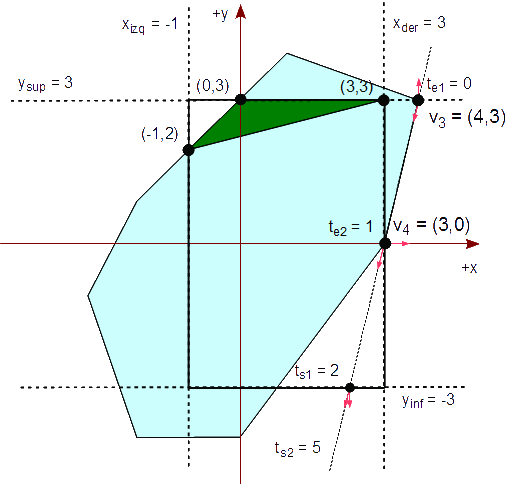
Figura 55 - Analizamos la tercera arista del polígono

Analicemos el tercer segmento formado por v₃v₄. Calculamos las cuatro intersecciones y las clasificamos a través de sus parámetros.

Δ_x = v_{4_x} - v_{3_x} = 3 - 4 = -1
Δ_y = v_{4_y} - v_{3_y} = 0 - 3 = -3

t_e₁ = -(v_{3_y} - y_sup) /  Δ_y = -( 3 - 3 ) / (-3)     = 0
t_e₂ =  (v_{3_x} - x_der) / -Δ_x =  ( 4 - 3 ) / -(-1)    = 1
t_s₁ =  (v_{3_y} - y_inf) / -Δ_y =  ( 3 - (-3) ) / -(-3) = 2
t_s₂ = -(v_{3_x} - x_izq) /  Δ_x = -( 4 - (-1) ) / (-1)  = 5

(x,y) = v₃ + t_e₂ * (Δ_x,Δ_y) = (4,3) + 1 * (-1,-3)
      = (3,0)

y lo agregamos a la lista resultante, Q. La lista resultante es ahora:

Q : { (-1,2), (3,3), (3,0) }

Como t_s₁ ≥ 1, agregamos el vértice final del segmento, (3,0), a la lista resultante que es ahora:

Q : { (-1,2), (3,3), (3,0), (3,0) }

Como t_s₂ ≥ 1, no agregamos un vértice de giro.

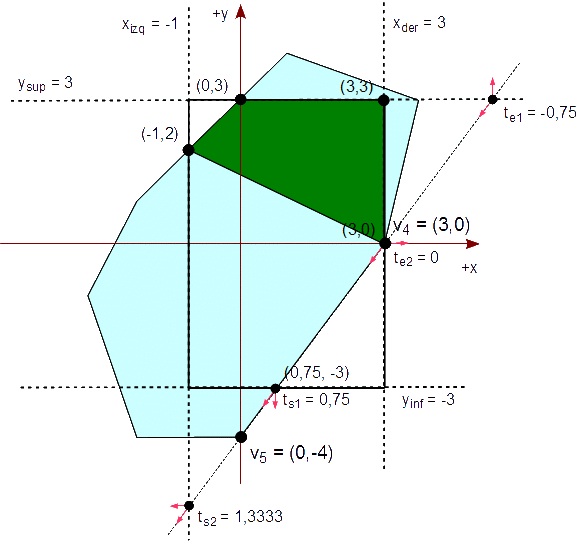
Figura 56 - Analizamos la cuarta arista del polígono

Analicemos el cuarto segmento formado por v₄v₅. Calculamos las cuatro intersecciones y las clasificamos a través de sus parámetros.

Δ_x = v_{5_x} - v_{4_x} =  0 - 3 = -3
Δ_y = v_{5_y} - v_{4_y} = -4 - 0 = -4

t_e₁ = -(v_{4_y} - y_sup) /  Δ_y = -( 0 - 3 ) / (-4)     = -0,75
t_e₂ =  (v_{4_x} - x_der) / -Δ_x =  ( 3 - 3 ) / -(-3)    =  0
t_s₁ =  (v_{4_y} - y_inf) / -Δ_y =  ( 0 - (-3) ) / -(-4) =  0,75
t_s₂ = -(v_{4_x} - x_izq) /  Δ_x = -( 3 - (-1) ) / (-3)  =  1,3333

Como t_s₂ > 0, t_e₂ ≤ t_s₁, 0 < t_s₁ y t_e₂ ≤ 1, el segmento es completa o parcialmente visible en el rectángulo de recorte. Como t_e₂ ≤ 0, agregamos el vértice inicial del segmento, (3,0), a la lista resultante que es ahora:

Q : { (-1,2), (3,3), (3,0), (3,0), (3,0) }

Como t_s₁ < 1, calculamos la intersección:

(x,y) = v₄ + t_s₁ * (Δ_x,Δ_y) = (3,0) + 0,75 * (-3,-4)
      = (0,75, -3)

y lo agregamos a la lista resultante, Q. La lista resultante es ahora:

Q : { (-1,2), (3,3), (3,0), (3,0), (3,0), (0,75, -3) }

Como t_s₂ ≥ 1, no agregamos un vértice de giro.

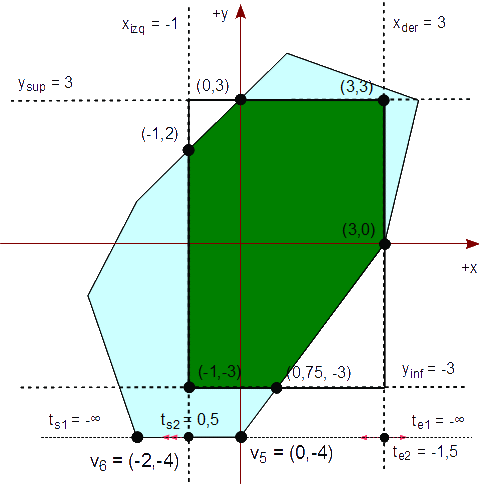
Figura 57 - Analizamos la quinta arista del polígono

Analicemos el quinto segmento formado por v₅v₆. Calculamos las cuatro intersecciones y las clasificamos a través de sus parámetros.

Δ_x = v_{6_x} - v_{5_x} = -2 - 0 = -2
Δ_y = v_{6_y} - v_{5_y} = -4 - (-4) = 0

t_e₁ = -∞
t_e₂ =  (v_{5_x} - x_der) / -Δ_x =  ( 0 - 3 ) / -(-2)    = -1,5
t_s₁ = -∞
t_s₂ = -(v_{5_x} - x_izq) /  Δ_x = -( 0 - (-1) ) / (-2)  =  0,5

Aunque t_s₂ > 0, t_s₁ < t_e₂ y por tanto, el segmento no es visible en el rectángulo de recorte. Como 0 < t_s₂ ≤ 1, agregamos el vértice de giro, (-1,-3) a la lista resultante, Q. La lista resultante es ahora:

Q : { (-1,2), (3,3), (3,0), (3,0), (3,0), (0,75, -3), (-1,-3) }

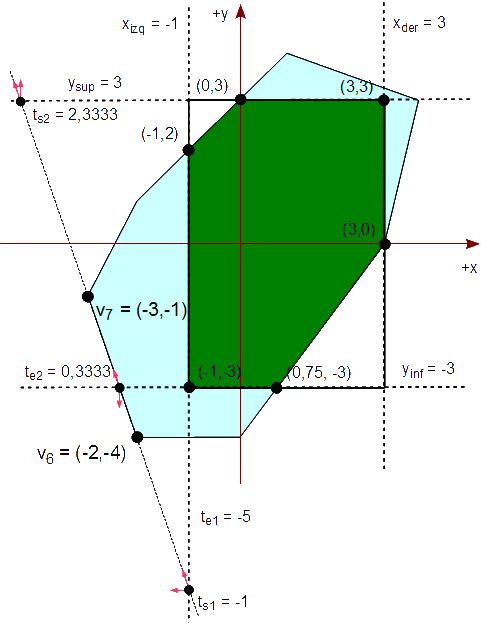
Figura 58 - Analizamos la sexta arista del polígono

Analicemos el sexto segmento formado por v₆v₇. Calculamos las cuatro intersecciones y las clasificamos a través de sus parámetros.

Δ_x = v_{7_x} - v_{6_x} = -3 - (-2) = -1
Δ_y = v_{7_y} - v_{6_y} = -1 - (-4) =  3

t_e₁ =  (v_{6_x} - x_der) / -Δ_x =  ( -2 - 3 ) / -(-1)   = -5
t_e₂ =  (v_{6_y} - y_inf) / -Δ_y =  ( -4 - (-3) ) / (-3) =  0,3333
t_s₁ = -(v_{6_x} - x_izq) /  Δ_x = -( -2 - (-1) ) / (-1) = -1
t_s₂ = -(v_{6_y} - y_sup) /  Δ_y = -( -4 - 3 ) / 3       =  2,3333

Aunque t_s₂ > 0, t_s₁ < t_e₂ y por tanto, el segmento no es visible en el rectángulo de recorte. Como t_s₂ > 1, no agregamos un vértice de giro. La lista resultante sigue siendo:

Q : { (-1,2), (3,3), (3,0), (3,0), (3,0), (0,75, -3), (-1,-3) }

Figura 59 - Analizamos la última arista del polígono

Analicemos el último segmento formado por v₇v₁. Calculamos las cuatro intersecciones y las clasificamos a través de sus parámetros.

Δ_x = v_{1_x} - v_{7_x} = -2 - (-3) = 1
Δ_y = v_{1_y} - v_{7_y} =  1 - (-1) = 2

t_e₁ =  (v_{7_y} - y_inf) / -Δ_y =  ( -1 - (-3) ) / (-2) = -2
t_e₂ = -(v_{7_x} - x_izq) /  Δ_x = -( -3 - (-1) ) / 1    =  2
t_s₁ = -(v_{7_y} - y_sup) /  Δ_y = -( -1 - 3 ) / 2       =  2
t_s₂ =  (v_{7_x} - x_der) / -Δ_x =  ( -3 - 3 ) / (-1)    =  6

Aunque t_s₂ > 0, t_e₂ ≥ t_s₁, y 0 < t_s₁, el segmento no es visible en el rectángulo de recorte ni se agrega ninguna intersección, porque t_e₂ > 1. Como t_s₂ > 1, tampoco agregamos un vértice de giro. La lista resultante sigue siendo:

Q : { (-1,2), (3,3), (3,0), (3,0), (3,0), (0,75, -3), (-1,-3) }

Como existen puntos contiguos repetidos en la lista de vértices del polígono resultante, nos interesaría eliminarlos. Al final, la lista resultante es:

{ (-1,2), (3,3), (3,0), (0,75, -3), (-1,-3) }

Algoritmo

Presentamos el algoritmo detallado y optimizado para Recortar() basado en el algoritmo presentado por Foley en su libro:

Polígono Recortar( Polígono P, Rectángulo R )
	1. Crear Polígono: Resultado ← vacío
	2. P.Agregar( P.v[1].x, P.v[1].y )  // Agregamos el primer vértice al final
	3. Para: i ← 1 hasta P.cantidad, repetir
		4. dx ← P.v[i+1].x - P.v[i].x
		5. dy ← P.v[i+1].y - P.v[i].y
		6. Si dx > 0, o Si dx = 0 y P.v[i].x > R.x_der, entonces
			7. x_e ← R.x_izq
			8. x_s ← R.x_der
		9. Si no, entonces
			10. x_e ← R.x_der
			11. x_s ← R.x_izq
		12. Si dy > 0, o Si dy = 0 y P.v[i].y > R.y_sup, entonces
			13. y_e ← R.y_inf
			14. y_s ← R.y_sup
		15. Si no, entonces
			16. y_e ← R.y_sup
			17. y_s ← R.y_inf
		18. Si dx ≠ 0, entonces
			19. tX_s ← ( x_s - P.v[i].x ) / dx
		20. Si no, compruebe Si R.x_izq ≤ P.v[i].x ≤ R.x_der, entonces
			21. tX_s ← ∞
		22. Si no, entonces
			23. tX_s ← -∞
		24. Si dy ≠ 0, entonces
			25. tY_s ← ( y_s - P.v[i].y ) / dy
		26. Si no, compruebe Si R.y_inf ≤ P.v[i].y ≤ R.y_sup, entonces
			27. tY_s ← ∞
		28. Si no, entonces
			29. tY_s ← -∞
		// Ordenamos los dos puntos salientes
		30. Si tX_s < tY_s, entonces
			31. t1_s ← tX_s
			32. t2_s ← tY_s
		33. Si no, entonces
			34. t1_s ← tY_s
			35. t2_s ← tX_s
		36. Si t2_s > 0, entonces  // Calculamos t2_e
			37. Si dx ≠ 0, entonces
				38. tX_e ← ( x_e - P.v[i].x ) / dx
			39. Si no, entonces
				40. tX_e ← -∞
			41. Si dy ≠ 0, entonces
				42. tY_e ← ( y_e - P.v[i].y ) / dy
			43. Si no, entonces
				44. tY_e ← -∞
			45. Si tX_e < tY_e, entonces
				46. t2_e ← tY_e
			47. Si no, entonces
				48. t2_e ← tX_e
			49. Si t1_s < t2_e, entonces  // El segmento no es visible
				50. Si 0 < t1_s ≤ 1, entonces  // Agregamos un vértice de giro
					51. Si tX_e < tY_e, entonces
						52. Resultado.Agregar( x_s, y_e )
					53. Si no, entonces
						54. Resultado.Agregar( x_e, y_s )
			
			55. Si no, entonces
				56. Si 0 < t1_s y t2_e ≤ 1, entonces
					57. Si 0 < t2_e, entonces  // Agregamos una intersección
						58. Si tX_e > tY_e, entonces
							59. Resultado.Agregar( x_e, P.v[i].y + tX_e * dy )
						60. Si no, entonces
							61. Resultado.Agregar( P.v[i].x + tY_e * dx, y_e )
					62. Si no, entonces  // Agregamos el vértice inicial
						63. Resultado.Agregar( P.v[i].x, P.v[i].y )
					64. Si t1_s < 1, entonces  // Agregamos una intersección
						65. Si tX_s < tY_s, entonces
							66. Resultado.Agregar( x_s, P.v[i].y + tX_s * dy )
						67. Si no, entonces
							68. Resultado.Agregar( P.v[i].x + tY_s * dx, y_s )
					
					69. Si no, entonces  // Agregamos el vértice final
						70. Resultado.Agregar( P.v[i+1].x, P.v[i+1].y )
			
			71. Si 0 < t2_s ≤ 1, entonces  // Agregamos un vértice de giro
				72. Resultado.Agregar( x_s, y_s )
		
	
	73. Terminar( Resultado )

Agregar() se refiere a la operación básica para agregar un punto al final de la lista de vértices de un polígono.

Algoritmo de Weiler-Atherton

Este algoritmo se ideó originalmente para determinar la visibilidad de polígonos. Sin embargo, también sirve para determinar la intersección de dos polígonos, lo que implica que este mismo algoritmo se puede aplicar para recortar un polígono en un polígono de recorte. La ventaja de este algoritmo, comparado con otros, es que sirve para recortar polígonos convexos o cóncavos en cualquier polígono de recorte que también puede ser convexo o cóncavo; incluso acepta polígonos con agujeros. El resultado de este algoritmo es uno o varios polígonos que representan las partes visibles e interiores al polígono de recorte. Se supone, para cada polígono, una lista de vértices ordenada en el sentido de las agujas del reloj para representar el exterior del polígono. Una ordenación en el sentido contrario de las agujas del reloj sirve para describir cualesquier agujeros que contenga el polígono.

La estrategia se basa en recorrer los vértices y aristas del polígono a recortar que sean interiores al polígono de recorte. Si la arista está a punto de salirse del polígono de recorte, entonces cambiamos el recorrido al polígono de recorte, para continuar con su lista de vértices y aristas. Esto sugiere que debemos determinar todos los puntos de intersección entre ambos polígonos, teniendo en cuenta cuáles son entrantes y cuáles son salientes. Aplicamos las siguientes reglas al llegar a un punto de intersección en nuestro recorrido:

Entrante: Recorra el polígono a recortar.
Saliente: Recorra el polígono de recorte.

Ambos recorridos se hacen en el sentido de las agujas del reloj.

Por lo tanto, el algoritmo se divide en dos partes principales consecutivas: el cálculo de todas las intersecciones y posteriormente el recorrido de todos los puntos, según las reglas descritas anteriormente, para generar los polígonos resultantes.

Para formar cada polígono recortado, comenzamos con un punto de intersección entrante, agregando los demás puntos recorridos según las reglas establecidas hasta reencontrar ese mismo punto de intersección del comienzo, así cerrando el polígono.

Como ocurre en el recorte, es posible que las aristas de ambos polígonos no se crucen y por tanto no existan puntos de intersección. Si esto ocurriere, tenemos tres posibles casos a considerar según el polígono a recortar, P, y el polígono de recorte, R:

P es interior a R, por lo que el resultado es P.
R es interior a P o que es lo mismo, P engloba R, por lo que el resultado es R.
P y R son polígonos que no se intersectan entre sí, ni en las aristas ni en sus interiores y por tanto no existe ningún polígono recortado resultante.

Ejemplo

Descripción

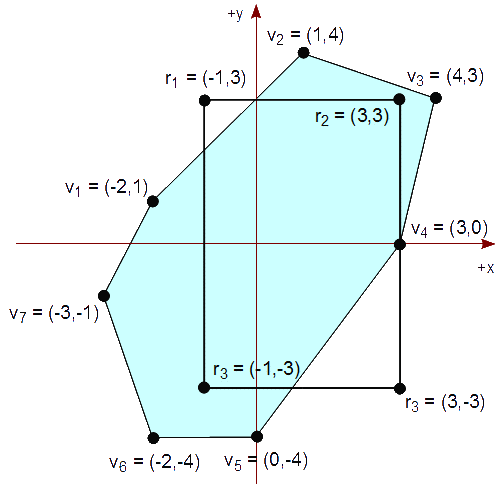
Retomamos el mismo ejemplo del método de Sutherland-Hodgman y Liang-Barsky. Tenemos un polígono de recorte, R, cuya lista de vértices es:

R : { (-1,3), (3,3), (3,-3), (-1,-3) }

Queremos uno varios polígonos, en tal polígono de recorte, a partir del polígono, P, descrito por la siguiente lista de vértices:

P : { (-2,1), (1,4), (4,3), (3,0), (0,-4), (-2,-4), (-3,-1) }

Solución

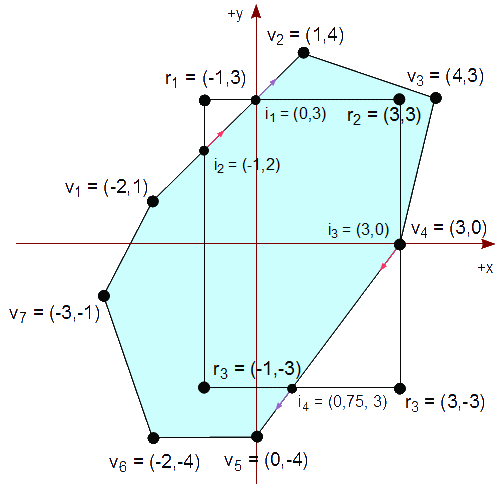
Figura 62 - Calculamos todas las intersecciones

Creamos una lista de polígonos, Q, que cada uno incluye una lista de vértices para representar los polígonos resultantes del recorte, inicialmente vacía:

Q₁ : {}

Antes de empezar el recorte de nuestro polígono, calculamos todos los puntos de intersección. Como tenemos que insertar estos puntos correctamente en las dos listas de vértices, P y R, para que ambas listas sigan el sentido de las agujas del reloj. Para realizar esta ordenación, calculamos y guardamos sus parámetros del segmento, t. Adicionalmente, necesitamos saber cuáles de estos puntos de intersección son entrantes (en rojo en la figura 62) y cuáles son salientes (en morado en la figura 62). Los puntos son:

i₁ = (  0,  3 )  ⇐  t = 0,6666  (saliente)
i₂ = ( -1,  2 )  ⇐  t = 0,3333  (entrante)
i₃ = (  3,  0 )  ⇐  t = 0       (entrante)
i₄ = (0,75, 3 )  ⇐  t = 0,75    (saliente)

Insertamos estos puntos de intersección correctamente en cada lista de vértices. i₁ e i₂ deben insertarse correctamente entre los vértices P.v₁ y P.v₂. Comparando los parámetros de i₁ e i₂, determinamos que el orden correcto es:

  v₁       i₂     i₁     v₂
(-2,1), (-1,2), (0,3), (1,4)
 t=0    t=0,33  t=0,66  t=1

El resultando de todas las inserciones correctas en las listas de vértices de ambos polígonos es:

P : { (-2,1), (-1,2), (0,3), (1,4), (4,3), (3,0), (3,0), (0,75, 3), (0,-4), (-2,-4), (-3,-1) }

R : { (-1,3), (0,3), (3,3), (3,0), (3,-3), (0,75, 3), (-1,-3), (-1,2) }

Seguimos el recorrido, pero llegamos al punto i₁ que es saliente. Según las reglas, debemos cambiar de lista de vértices para continuar el recorrido en R. Agregando este punto i₁, por el momento, Q₁ contiene la siguiente lista:

Q₁ : { (-1,2), (0,3) }

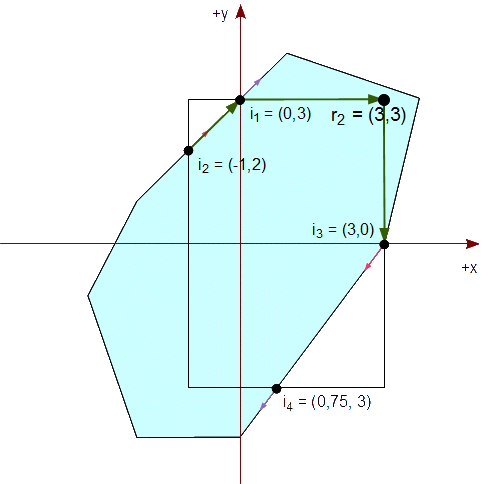
Figura 64 - Seguimos con el recorrido de R

Ahora, seguimos con el recorrido del polígono, R. Para ello, buscamos el punto de intersección saliente, i₁, en la lista de R. Recorriendo R, nos encontramos con el vértice, R.r₂, el cual agregamos a Q₁. El siguiente punto es una intersección entrante, i₃, por lo que debemos cambiar a la lista de vértices del polígono, P. Ahora la lista de vértices, Q₁, es:

Q₁ : { (-1,2), (0,3), (3,3), (3,0) }

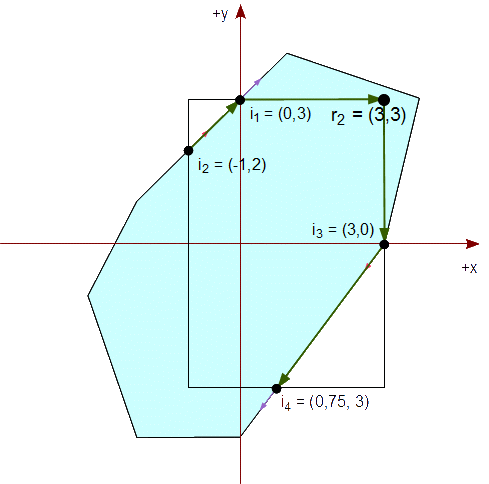
Figura 65 - Seguimos con el recorrido de P

Al saltar al polígono, P, buscamos el punto de intersección, i₃. Siguiendo la lista de P, a partir de i₃, nos encontramos con el punto de intersección saliente, i₄, el cual agregamos a Q₁. Como se trata de un punto de intersección saliente, debemos cambiar a la lista de vértices del polígono, R. Por ahora la lista de vértices, Q₁, es:

Q₁ : { (-1,2), (0,3), (3,3), (3,0), (0,75, 3 ) }

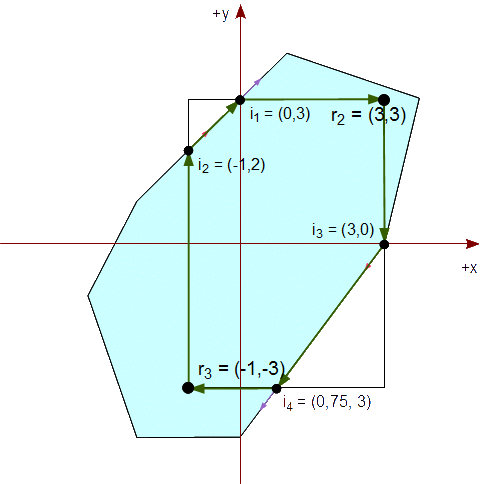
Figura 66 - Seguimos con el recorrido de R

Con la lista de vértices, R, buscamos el punto de intersección, i₄. Siguiendo la lista de R, a partir de i₄, nos encontramos con el vértice original, R.r₃, el cual agregamos a Q₁. El siguiente punto en R es de intersección entrante, i₁, que también se debería agregar a Q₁, pero ya lo visitamos previamente; y por tanto, se agregó en una etapa anterior del algoritmo. Como se trata de un punto de intersección entrante, debemos cambiar a la lista de vértices del polígono, P. Terminamos la lista de vértices, Q₁, que queda así:

Q₁ : { (-1,2), (0,3), (3,3), (3,0), (0,75, 3 ), (-1,-3) }

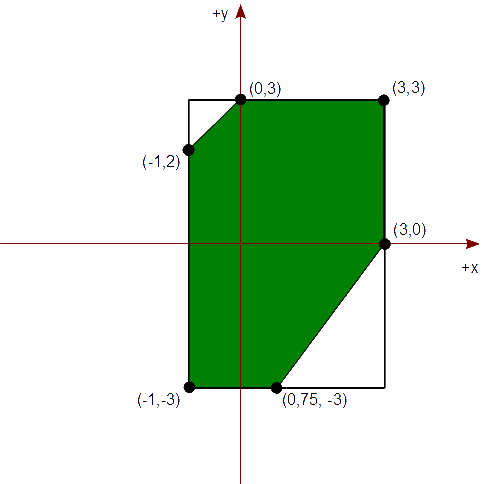
Al terminar un polígono recortado, volvemos a comenzar el algoritmo con la lista de vértices, P. Buscamos el siguiente punto de intersección entrante que no hayamos visitado, ni por lo tanto hayamos agregado al polígono de recorte, previamente. Como todos los puntos entrantes han sido visitados y usados anteriormente, finalizamos el recorte, dando lugar al polígono resultante, Q, que queda así:

Q : { (-1,2), (0,3), (3,3), (3,0), (0,75, 3 ), (-1,-3) }

Algoritmo

El algoritmo hace uso de cierta información que agruparemos en la siguiente estructura especial, definida así:

PuntoInfo
{
  real t;
  Punto vértice;
  booleano entrante;
}

Esta información se asociará a los puntos de intersección que calcularemos. Como el algoritmo debe distinguir entre un punto original de un polígono dado y un punto de intersección calculado, agregaremos una propiedad a Punto llamada original; si es verdadero, entonces se trata de un punto original, y falso indicará que es una intersección. También agregamos otra propiedad a Punto llamada visitado; si es verdadero, entonces hemos procesado este punto en el algoritmo de la intersección, y falso indicará que aún está por procesar.

Presentamos el algoritmo para Recortar() que acepta cualquier tipo de polígono convexo o cóncavo cerrado:

ListaPolígonos Recortar( Polígono P, Polígono R )
	1. Crear ListaPolígonos: Resultado ← vacía
	2. P.Agregar( P.v[1] )  // Agregamos el primer vértice al final
	3. R.Agregar( R.v[1] )
	4. ExistenIntersecciones ← Calcular_Intersecciones( P, R )
	5. Si ExistenIntersecciones = verdadero, entonces
		6. Resultado ← Intersectar( P, R, Resultado )
	7. Si no, entonces
		8. ContienePunto ← Acepta( P, R.v[1] )
		9. Si ContienePunto = verdadero, entonces
			10. Resultado ← R
		11. Si no, entonces
			12. ContienePunto ← Acepta( R, P.v[1] )
			13. Si ContienePunto = verdadero, entonces
				14. Resultado ← P
			15. Si no, entonces
				16. Resultado ← vacía
	17. Terminar( Resultado )

Exponemos el algoritmo de Calcular_Intersecciones() para calcular los puntos de intersección de las aristas entre los dos polígonos. Simultáneamente, agregamos estos puntos de intersección a los dos polígonos. Adicionalmente indicamos cuáles puntos son entrantes y cuáles son salientes.

booleano Calcular_Intersecciones( ref Polígono P, ref Polígono R )
	1. ExistenIntersecciones ← falso
	2. A ← P.v₁
	3. B ← Siguiente_Original( P, A )
	4. Mientras que, B ≠ P.v₁
		5. C ← R.v₁
		6. D ← Siguiente_Original( R, C )
		7. Mientras que, D ≠ R.v₁, repetir
			8. t_p ← Calcular_Parámetro( A, B, C, D )
			9. Si 0 ≤ t_p ≤ 1, entonces
				10. t_r ← Calcular_Parámetro( C, D, A, B )
				11. Si 0 ≤ t_r ≤ 1, entonces
					12. ExistenIntersecciones ← verdadero
					13. nuevo.vértice ← A + t_p*(B-A)
					14. nuevo.vértice.original ← falso
					15. nuevo.t ← t_p
					16. nuevo.entrante ← Es_Entrante( A, B, C, D )
					17. Insertar( P, A, B, nuevo )
					18. nuevo.t ← t_r
					19. Insertar( Q, C, D, nuevo )
			20. C ← D
			21. D ← Siguiente_Original( R, C )
		22. A ← B
		23. B ← Siguiente_Original( P, A )
	24. Terminar( ExistenIntersecciones )

El algoritmo de Siguiente_Original() requiere un polígono y un punto que pertenece a tal polígono. Recorrerá todos los puntos en busca del siguiente que es un vértice - un punto original del polígono.

Punto Siguiente_Original( Polígono P, Punto A )
	1. Resultado ← P.Siguiente( A )
	2. Mientras que, Resultado.original = falso, repetir
		3. Resultado ← P.Siguiente( Resultado )
	4. Terminar( Resultado )

Hacemos uso del algoritmo básico Siguiente() que obtendrá el siguiente vértice en la lista que forma el polígono.

El algoritmo para Calcular_Parámetro() requiere los puntos extremos de cada segmento para calcular el valor del parámetro del primer segmento del punto de intersección de ambos segmentos.

real Calcular_Parámetro( Punto P0, Punto P1, Punto Q0, Punto Q1 )
	1. N ← ( Q0_y - Q1_y, Q1_x - Q0_x )
	2. numerador ← N⋅(P0 - Q0)
	3. denominador ← -N⋅(P1 - P0)
	4. Si denominador ≠ 0, entonces
		5. t ← numerador / denominador
	6. Si no, entonces
		7. t ← ∞
	8. Terminar( t )

He aquí el algoritmo de Es_Entrante(), que determina si el segmento, descrito por el vector U, es entrante (verdadero) al cruzar la arista descrita por el vector V. Esto implica que su punto de intersección, tambié es entrante.

booleano Es_Entrante( Vector U, Vector V )
	1. N ← ( -V_y, V_x )
	2. denominador ← N⋅U
	3. Si denominador < 0, entonces
		4. Terminar( verdadero )
	5. Si no, entonces
		6.Terminar( falso )

El siguiente algoritmo describe Insertar(), que acepta un polígono, dos puntos extremos de una arista, y el nuevo punto a insertar correctamente.

Insertar( ref Polígono P, Punto A, Punto B, PuntoInfo nuevo )
	1. Actual ← A
	2. Sig ← P.Siguiente( A )
	3. terminar ← falso
	4. Mientras que, terminar = falso  y  Sig.original = falso, repetir
		5. Si nuevo.t < Sig.t, entonces
			6. P.Insertar_Nuevo( Actual, nuevo )
			7. terminar ← verdadero
		8. Si no, entonces
			9. Actual ← Sig
			10. Sig ← P.Siguiente( Actual )
		11. Resultado ← P.Siguiente( Resultado )
	12. P.Insertar_Nuevo( Actual, nuevo )
	13. Terminar

El algoritmo básico del polígono, Insertar_Nuevo(), sirve para agregar un nuevo punto a ello, justo después del punto indicado.

Exponemos el algoritmo de Intersectar() para determinar los polígonos de intersección entre dos polígonos dados.

ListaPolígonos Intersectar( Polígono P, Polígono R )
	1. Crear ListaPolígonos: Actual ← { P, R }   // Actual[1] = P, Actual[2] = R
	2. Crear ListaPolígonos: Resultado ← vacía
	3. Crear Polígono: Auxiliar ← vacío
	4. índice ← Buscar_Punto_Entrante_No_Visitado( P )
	5. Mientras que, índice > 0, repetir
		6. n ← 1
		7. Mientras que, Actual[n].v[índice].visitado = falso, repetir
			8. Actual[n].v[índice].visitado = verdadero
			9. Auxiliar.Agregar( Actual[n].v[índice].vértice )
			10. Si Actual[n].v[índice].original = falso, entonces
				11. Si Actual[n].v[índice].entrante = falso, entonces  // Cambio de polígono
					12. n_ant ← n
					13. Si n = 1, entonces
						14. n ← 2
					15. Si no, entonces
						16. n ← 1
					17. índice ← Buscar_Punto( Actual[n], Actual[n_ant].v[índice].vértice )
			18. índice ← índice + 1
			19. Si índice > Actual[n].Cantidad_Vértices(), entonces
				20. índice ← 1
		21. Resultado.AgregarPolígono( Auxiliar )
		22. Auxiliar.Vaciar()
		23. índice ← Buscar_Punto_Entrante_No_Visitado( P )
	24. Terminar( Resultado )

He aquí el algoritmo de Buscar_Punto_Entrante_No_Visitado() para encontrar el punto entrante sin marcar como visitado del polígono dado. El algoritmo retornará el índice al punto encontrado o 0 (cero), para indicar que no existe ninguno.

entero Buscar_Punto_Entrante_No_Visitado( Polígono P )
	1. Para: índice ← 1 hasta P.Cantidad_Vértices(), repetir
		2. Si P.v[índice].original = falso  y  Si P.v[índice].entrante = verdadero  y  Si P.v[índice].visitado = falso, entonces
			3. Terminar( índice )
	4. Terminar( 0 )

Presentamos el algoritmo de Buscar_Punto() para encontrar el punto indicado en el polígono dado. El algoritmo retornará el índice al punto encontrado o 0 (cero), para indicar que no se encontró.

entero Buscar_Punto( Polígono P, Punto I )
	1. Para: índice ← 1 hasta P.Cantidad_Vértices(), repetir
		2. Si P.v[índice].vértice = I, entonces
			3. Terminar( índice )
	4. Terminar( 0 )

Observaciones

Para aquellas implementaciones del algoritmo de Sutherland-Hodgman para hardware, podemos descomponer este algoritmo en varias etapas. Cada etapa manipula un vértice para cada arista y así no tenemos que usar una lista de vértices intermediaria. Esta mejora se puede conseguir con un procesamiento paralelo o con un solo procesador configurado por etapas. Si un vértice es validado al terminar todas las etapas de recorte, entonces se agrega a la lista final de vértices. De lo contrario, el vértice no continúa en el procesamiento.

Una mejora del algoritmo de Weiler-Atherton es mantener una lista de puntos entrantes, en lugar de buscarlos en el polígono a recortar. Dejamos su implementación como un ejercicio. También podemos usar este algoritmo para conseguir la unión de dos polígonos. En lugar de tratar los puntos de intersección entrantes como el principio del polígono resultante y los salientes para alternar entre polígonos, invertimos esta lógica. Tratamos los puntos de intersección entrantes para alternar entre polígonos y los salientes como el principio del polígono resultante. También dejamos esta implementación como un ejercicio.

Concluyendo, el algoritmo de Nicholl-Lee-Nicholl es actualmente el mejor de los algoritmos de recorte de segmentos que hemos tratado. Los algoritmos de Liang-Barsky y Cohen-Sutherland siguen siendo populares, y en este último caso, el algoritmo es muy fácil de implementar. Estos tres algoritmos se basan en un rectángulo vertical de recorte. El algoritmo de Cyrus-Beck se basa en un polígono convexo de recorte, pero requiere varios cálculos costosos en comparación con los algoritmos anteriores. Para los algoritmos de recorte de polígonos, los algoritmos presentados son fáciles de entender y de describir, pero no son recomendados porque requieren varios cálculos, y además existen otros algoritmos de mejor rendimiento.

Volviendo a nuestro esquema de las etapas del procesamiento de datos geométricos a colores asignados a cada píxel de la pantalla o puntos de impresión en papel, agregamos el proceso de recorte como una nueva etapa. Nuestro esquema es ahora el siguiente:

Ejercicios

Enlace al paquete de este capítulo.

Como mencionamos en la explicación del algoritmo de Cohen-Sutherland, podemos mejorarlo un poco para que no recalcule la pendiente de la intersección en cada iteración.
1. Implemente el algoritmo original,
2. Implemente otra versión del algoritmo con la mejora mencionada, y
3. Escriba un programa para comparar el rendimiento de ambos algoritmos. Para el programa, cree aleatoriamente varios segmentos - decenas de millares - para pasarlos por los dos algoritmos de a) y b) para ser recortados. Cronometre los procesamientos de ambos algoritmos y muestre los resultados de la comparativa.
Optimice el algoritmo de Nicholl-Lee-Nicholl para reusar multiplicaciones y restas y así no hay que invocar a Izquierda(), ni a Derecha(), ni tampoco a Intersección_Vertical() ni a Intersección_Horizontal(). Por ejemplo, en el algoritmo de Recortar_Interior(), podemos sustituir el comienzo con los siguientes pasos, para no tener que usar Izquierda():
```
	2. QPX ← Q.x - P.x
	3. QPY ← Q.y - P.y
	4. A ← R.x_izq - P.x
	5. B ← R.y_sup - P.y
	6. Si A*QPX + B*QPY > 0, entonces
```
Implemente las mejoras mencionadas anteriormente para el algoritmo Weiler-Atherton. Cree otra lista de puntos, o referencias a los puntos, para guardar las intersecciones entrantes, que previamente hemos calculado. Esta lista contendrá menos puntos que la lista de los vértices originales y puntos de intersección. Ahora, sólo tendremos que consultar esta lista, en lugar de buscar las intersecciones entre todos los puntos, para conseguir aquellas intersecciones entrantes aún sin visitar.
Como mencionamos anteriormente, podemos usar el algoritmo de Weiler-Atherton para el modelado. Con las operaciones básicas de conjuntos - unión, intersección, y diferencia - podemos construir nuevas figuras geométricas a partir de dos figuras básicas, como mínimo.

Ejercicio 4 - Polígonos A y B
- A ∪ B. Para la unión, buscamos cualesquier intersecciones entre los dos polígonos A y B. Comenzamos con el recorrido de A, el polígono a recortar, o de B, el polígono de recorte. Cambiamos de polígono al encontrarnos con intersecciones.
  
  Ejercicio 4 - Unión de A y B
- A ∩ B. La intersección es justamente el algoritmo original de recorte de Weiler-Atherton. Recorremos el polígono A al encontrarnos con las intersecciones entrantes y recorremos el polígono B al encontrarnos con las intersecciones salientes.
  
  Ejercicio 4 - Intersección de A y B
- A − B. Para la diferencia, comenzamos con el polígono A y eliminamos partes de ello con el polígono B. Usando el algoritmo de Weiler-Atherton, recorremos el polígono A al encontrarnos con las intersecciones salientes y recorremos el polígono B al encontrarnos con las intersecciones entrantes.
  
  Ejercicio 4 - Diferencia de A y B
Cree un programa que permita al usuario generar polígonos con estas operaciones.