Capítulo 2 - Trazar Ecuaciones
Para comenzar, veamos un ejemplo práctico del uso de gráficos: trazar la gráfica de una ecuación.
En este capítulo trazaremos la ecuación: y = 3x2 - 6.
Cambio de Coordenadas I
La ventaja que tenemos es que el ordenador no se "cansará" al calcular todos los valores que requerimos, por lo que no tendremos problemas de precisión. Por otro lado, estamos intentado representar una imagen de dimensiones infinitas - el plano cartesiano, debido a los valores de x que son infinitos, en un área de dimensiones finitas - la pantalla. Por lo tanto, debemos representar la gráfica ajustándonos a las dimensiones de nuestra pantalla. Las dimensiones de la imagen equivalen a la resolución gráfica establecida. Para este ejemplo, usaremos una resolución de 800 x 600.
Ahora tenemos que pensar qué representa cada píxel que activemos - demos color.
Si establecemos que cada píxel equivale a una unidad matemática, entonces no obtendremos una imagen presentable.
Hay que tener en cuenta que las unidades matemáticas no tienen por qué
ser valores enteros, mientras que los píxeles sí deben serlos.
Lo que tenemos que hacer es decidir los valores mínimo y máximo a usarse en la ecuación.
Digamos que queremos ver parte de la gráfica usando los valores de
Primeramente, debemos cambiar la escala o longitud: 6 (=3-(-3)) unidades cartesianas a 800 píxeles (el número de columnas); esto implica que existen 6/800 unidades cartesianas por cada píxel, que es lo mismo que decir: 0,0075 unidades/píxel. Dicho de otro modo, cada píxel representará 0,0075 unidades cartesianas. Miremos unos cuantos valores, para ilustrar este concepto:
| Unidades Cartesianas |
Píxeles |
| -3,0000 |
0 |
| -2,9925 |
1 |
| -2,9850 |
2 |
| -2,9775 |
3 |
| . . . |
. . . |
| 2,9700 |
796 |
| 2,9775 |
797 |
| 2,9850 |
798 |
| 2,9925 |
799 |
También podemos establecer la relación realizando la operación inversa: 800/6 = 133,3333 píxeles/unidad. Aquí podemos ver que sería algo difícil representar 133,3333 píxeles, ya que los píxeles son siempre enteros. Esto implica que obtendremos errores al aproximarnos a un número entero; en este caso, 133 (≅133,3333).
Cual sea la relación, podemos averiguar un píxel determinado a partir de una coordenada cartesiana determinada, y viceversa.
Por ejemplo, si tenemos la coordenada-X de un píxel,
6 unidades |xu - xui| unidades ------------- = ---------------------- ⇒ 800 píxeles |345 - xpi| píxeles |345 - 0| píxeles * 0,0075 unidades/píxel = |x - (-3)| unidades ⇒ x = -0,4125 unidades.
Por otro lado, podemos averiguar el píxel correspondiente a la coordenada-X, xu = -2,0000, aplicando la simple regla de tres:
800 píxeles |xp - xpi| píxeles ------------- = -------------------------- ⇒ 6 unidades |-2,0000 - xui| unidades 1,000 unidad * 133,3333 píxeles/unidad = |xp - 0| píxeles ⇒ x = 133,3333 píxeles ⇒ x = 133 píxeles.
Del mismo modo, tenemos que averiguar los valores de y en unidades cartesianas correspondientes con los valores en píxeles.
El número de filas es 600 píxeles, según nuestra resolución que hemos elegido.
Ya que los valores del eje-Y son imaginarios, éstos pueden ser calculados.
Por esta razón, el conjunto de valores puede ser ajustado según los valores inicial y final del eje-X.
Con
| Unidades Cartesianas |
Píxeles |
| -6,0000 |
0 |
| -5,9550 |
1 |
| -5,9100 |
2 |
| -5,8650 |
3 |
| . . . |
. . . |
| 20,8200 |
596 |
| 20,8650 |
597 |
| 20,9100 |
598 |
| 20,9550 |
599 |
Calculemos el píxel que corresponda al valor en unidades cartesianas de
600 píxeles |yp - ypi| píxeles ------------- = -------------------------- ⇒ 27 unidades |6,0000 - yui| unidades |6,0000 - (-6)| unidades * 22,2222 píxeles/unidad = |yp - 0| píxeles ⇒ y = 266,6666 píxeles ⇒ y = 267 píxeles.
Por lo tanto, la coordenada
Observaciones
Es posible que el lector haya hecho unos cuantos cálculos u observaciones y haya descubierto que,
-
Aunque tengamos una serie de píxeles con coordenadas continuas a lo largo del eje-X, las coordenadas del eje-Y no son contiguas, en su mayor parte.
Esto depende de la gráfica y, por tanto, del tipo de ecuación.
Si estuviéramos trazando la gráfica de una ecuación lineal de poca pendiente:
y = mx + b, m : [0,1], donde m es la pendiente, entonces todos los valores de cada coordenada(xp, yp) serían contiguos. Perdemos precisión en la coordenada-Y, al ser precisos en la coordenada-X, y viceversa. Un arreglo que podemos hacer es trazar líneas continuas entre cada píxel que calculemos. Esto implica que cada píxel se convertirá en un vértice para luego ser unidos con líneas. En resumen, aproximamos la curva de la gráfica usando líneas. Esto queda mejor explicado en la siguiente sección: Explicación Detallada. -
Las fórmulas presentadas no sirven para hallar los valores finales de la coordenada x ni y.
En nuestro ejemplo, estos valores corresponderían a:
xuf = 3 eyuf = 21; sus homólogos en píxeles son:xpf = 800 eypf = 600. Claro está, estos valores son 1 píxel más allá de la resolución en cada dirección. Esto es debido a que estamos aproximando un intervalo de valores (cartesianos) como un valor único (píxel). Por ejemplo, el valor xp = 4 representa el conjunto de valoresxu : [-2,9700, -2,9625). Si nos fijamos, el valor limitante, -2,9625, no pertenece a este intervalo, pero todos los valores anteriores pertenecientes sí son aproximados porxp = 4. Cuando llegamos al último intervalo,xu : [2,9925, 3,0000), notamos que el último valorxuf = 3 no forma parte de este intervalo, aunque por defecto tiene la misma representación. No podemos hacer mucho para corregir esta inexactitud; simplemente se nos han acabado las columnas. Sin embargo, podemos hacer una de estas dos posiblidades para intentar arreglarlo: -
Trazar una línea usando como la última coordenada,
xpf = 800 (el siguiente valor). La mayoría de los sistemas gráficos permitirá dibujar en zonas inexistentes ya que éstos realizan la tarea de eliminar píxeles "sobrantes" o "irrepresentables". Con esto, conseguiremos la parte de la línea en el eje-Y. Aunque no lleguemos justamente a la coordenadaxpf, llegaremos lo suficientemente cerca. - Invertir el proceso de trazado. En vez de averiguar el valor de y a partir del valor de x y posteriormente obtener su correspondencia en píxeles, trataremos de averiguar los valores de y que pertenezcan a sus complementos de x.
Explicación Detallada
Como ya se ha explicado, los píxeles representan intervalos de valores.
En nuestro ejemplo,
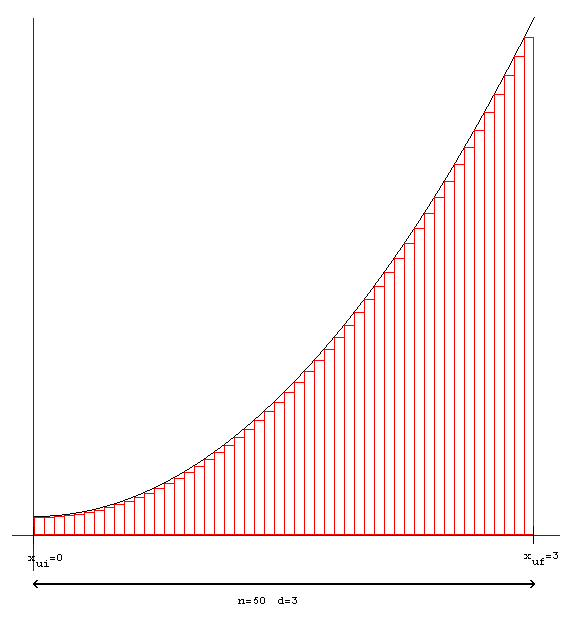
En la Figura 1, cada rectángulo representa la coordenada xp del píxel. La anchura de cada rectángulo indica el recorrido de valores de xu que representa. Del mismo modo, actúa cada rectángulo para la coordenada yp. Esto se muestra claramente en la Figura 2:
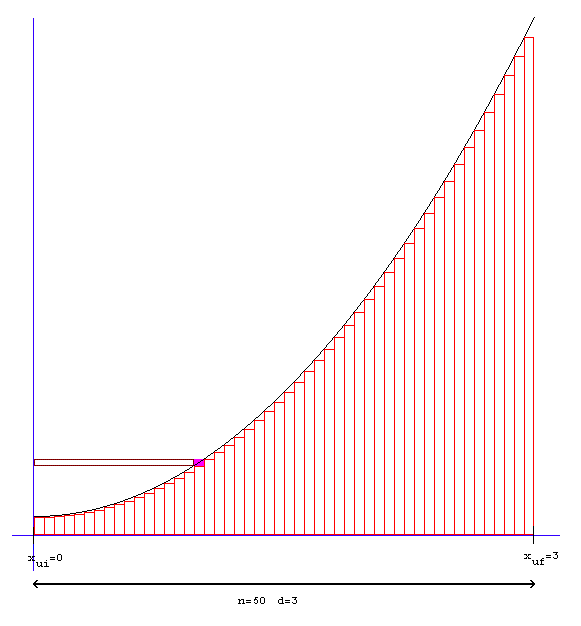
El área de color violeta representa el píxel (xp,yp) para los recorridos de los valores de xu e yu.
Para aquellos lectores que tengan conocimientos de cálculo diferencial, ambas figuras asemejan la aproximación del área debajo de una curva. Al área real (precisa) la llamamos una integral. Sin embargo, nosotros sólo calculamos los valores para crear una serie y no una suma, como es el método de la suma de Riemann. En la Figura 2, tenemos los datos suficientes para comprobar nuestro método:
n : Número de particiones = rectángulos, d : Distancia de nuestro intervalo. xui : Valor inicial de nuestro intervalo.
Usando los valores en la gráfica, obtenemos:
x0 = [xui, xui + 3/50) x1 = [xui + 3/50, xui + 6/50) x2 = [xui + 6/50, xui + 9/50) ... xa = [xui + a*d / n, xui + (a+1)*d / n), a = 0,1,2,...,n-1
a representa el número de columnas de nuestra resolución gráfica. Así es como elegimos a nuestros valores en la coordenada x. Para los valores en la coordenada y, aplicamos nuestra ecuación teniendo en cuenta el número de particiones a lo largo del eje-Y. Por esta razón debemos realizar un cambio de coordenadas del plano cartesiano al plano gráfico en píxeles.
Al ver ambas figuras, podemos observar que tal método nos es suficiente para coordenadas que no se distancien mucho entre sí. Observando la curva hacia la derecha, nos damos cuenta de que los valores de cada partición se alejan bastante, y por tanto optamos por trazar líneas entre cada píxel. Esto es análogo al método trapezoidal para la aproximación de un área debajo de una curva. Es decir, en vez de usar rectángulos, usamos trapezoides.
La otra observación de ambas figuras es la representación del último valor xuf. La curva continúa, pero la partición no puede representar xuf. Una alternativa es invertir el proceso de aproximación. En vez de usar el método de rectángulos inscritos, usar rectángulos circunscritos o exteriores en vez de interiores. Generalmente no podemos decidir cuál método nos saldrá más rentable, ya que depende de la ecuación que queramos representar y por tanto de la forma de la gráfica.
Otro método que podemos implementar es realizar los cálculos inversos: a partir de coordenadas en píxeles, averiguar si pertenecen a la ecuación en unidades cartesianas. Sin embargo, para usar este método, tendríamos que comprobar todos los píxeles en la pantalla. Para crear imágenes de fractales, sí haremos uso de este método. Para algunos fractales, la imagen no es el trazado de la ecuación, sino que se basa en una ecuación. Este caso lo veremos más detenidamente en el siguiente capítulo: Fractales.
Cambio de Coordenadas II
Aún no hemos acabado con nuestra gráfica. Al calcular los valores y cambios de escala, lo hemos hecho en base a una condición: la orientación del sistema de coordenadas del plano cartesiano sea la misma que el sistema gráfico; en nuestro caso, es la pantalla. Generalmente, los sistemas gráficos comienzan por la coordenada (0,0) en la esquina superior izquierda. Esto implica que la orientación en el eje-X es positiva de izquierda a derecha y en el eje-Y es positiva de arriba a abajo. En el plano cartesiano, por regla común, la orientación positiva en el eje-X es de izquierda a derecha y en el eje-Y de abajo a arriba. Como podemos observar, la orientación en el eje-X es la misma que en el plano cartesiano: de izquierda a derecha, pero no en el eje-Y. Debido a esta diferencia, debemos asegurarnos de la orientación; de lo contrario, veremos nuestros trazados en el sentido inverso, como si fueran vistos en un espejo.
Para arreglar las orientaciones, necesitamos arreglar nuestras fórmulas. Como ya se ha dicho, la orientación en el eje-X no necesita cambios, pero el eje-Y, sí los necesita. Usaremos el mismo ejemplo, yu = 6,0000. El píxel yp en su orientación correcta se calcula de la siguiente forma:
600 píxeles |(ypi + alturap) - yp| píxeles ------------- = ------------------------------- ⇒ 27 unidades (6,0000 - yui) unidades |6,0000 - (-6)| unidades * 22,2222 píxeles/unidad = |(0+600) - yp| píxeles ⇒ yp = 333,3333 píxeles ⇒ yp = 333 píxeles.
alturap : es la altura o el número de filas de nuestra resolución. Aplicando un poco de lógica y álgebra, podemos usar la siguiente fórmula:
600 píxeles |(ypf + 1) - yp| píxeles ------------- = -------------------------- ⇒ 27 unidades |6,0000 - yui| unidades |6,0000 - (-6)| unidades * 22,2222 píxeles/unidad = |(599+1) - yp| píxeles ⇒ yp = 333,3333 píxeles ⇒ yp = 333 píxeles.
Al final, el píxel (133,333) representa correctamente el punto (-2,6), en la mayoría de los sistemas gráficos.
Fórmulas
| xpi |
Valor inicial de la coordenada X en píxeles |
| ypi |
Valor inicial de la coordenada Y en píxeles |
| xpf |
Valor final de la coordenada X en píxeles |
| ypf |
Valor final de la coordenada Y en píxeles |
| xp |
Valor arbitrario de la coordenada X en píxeles |
| yp |
Valor arbitrario de la coordenada Y en píxeles |
| xui |
Valor inicial de la coordenada X en unidades cartesianas |
| yui |
Valor inicial de la coordenada Y en unidades cartesianas |
| xuf |
Valor final de la coordenada X en unidades cartesianas |
| yuf |
Valor final de la coordenada Y en unidades cartesianas |
| xu |
Valor arbitrario de la coordenada X en unidades cartesianas |
| yu |
Valor arbitrario de la coordenada Y en unidades cartesianas |
| anchurap |xpf - xpi + 1| |
Número de columnas a representar en píxeles |
| alturap |ypf - ypi + 1| |
Número de filas a representar en píxeles |
| anchurau |xuf - xui| |
Distancia entre los valores final e inicial de las coordenadas X en unidades cartesianas |
| alturau |yuf - yui| |
Distancia entre los valores final e inicial de las coordenadas Y en unidades cartesianas |
anchurau |xu - xui| ---------- = ----------- anchurap |xp - xpi| |
Para hallar el valor de xu conociendo el valor de xp |
alturap |(ypf - ypi + 1) - yp| --------- = ----------------------- alturau |yu - yui| |
Para hallar el valor de yp conociendo el valor de yu si la orientación en píxeles es de sentido contrario a la del plano cartesiano |
Algoritmo
Aquí exponemos el algoritmo para el trazado de una ecuación:
- Inicializar valores para:
xui, xuf, yui, yuf, xpi, xpf, ypi, ypfanchurau ← |xuf - xui|alturau ← |yuf - yui|anchurap ← |xpf - xpi + 1|alturap ← |ypf - ypi + 1|dxup ← anchurau / anchurapdypu ← alturap / alturauxu ← xuiyu ← función( xu )x_origp ← xpiy_origp ← ypf + 1 - dyup * |yu - yui|- Bucle:
xp ← xpi+1hastaxpfcon incremento de 1xu ← xu + dxupyu ← función( xu )yp ← ypf + 1 - dyup * |yu - yui|Dibujar_Línea( x_origp, y_origp, xp, yp )x_origp ← xpy_origp ← yp
función() es la ecuación cuya gráfica queremos trazar. La función Dibujar_Línea() hace alusión a la función básica de cualquier API o biblioteca gráfica, para trazar una línea recta desde una coordenada de píxeles a otra.
Ejercicios
Enlace al paquete de este capítulo.
-
Escriba, para cada ecuación, un programa que trace las gráficas de las siguientes ecuaciones y según las restricciones dadas:
-
y(x) = 0,5x4 - 2x3 + 0,33x2 - 0,75x + 1,
Restricciones:x = [-1, +2], y = [y(2), y(-1)],
Resolución: 100 x 100.
Ejercicio 1a -
y(x) = (1,5x3 - 2,6x2 + 3,3x - 10) / (x2 - 1,5x + 0,5),
Restricciones:x = [0, +2], y
Resolución: 300 x 300,
Observación: la ecuación contiene dos asíntotas verticales,x1yx2.xpara que la ecuación no sea indeterminada enx = x1x = x2.
(Pista: Precalcula,x2 - 1,5x + 0,5 = 0,
Ejercicio 1b -
Si
x < 1,y(x) = 1 - x2,1 ≤ x ≤ 9,y(x) = ln x,x > 9,y(x) = cos x,
Restricciones:x = [-1, +12], y
Resolución: 600 x 600.
Ejercicio 1c -
y(x) = |6 - x2|,
Restricciones:x = [-5, +5], y = [0, +6]
Resolución: 300 x 300 para la gráfica, pero centrado en una resolución total de la ventana, portal, o zona de dibujo de 500 x 500. Es decir, la gráfica debe dibujarse en unas dimensiones de 300 x 300, pero las dimensiones de la ventana o zona de dibujo son de 500 x 500. La gráfica debe estar centrada con respecto a la ventana.
Ejercicio 1d
-
- Elija dos de las ecuaciones anteriores y reescriba sus programas para que trace las curvas usando el método descrito en el último párrafo de la sección Observaciones, bajo b)2.. Esto es, trace la ecuación a partir de valores dados para yp en vez de xp. Compare las gráficas obtenidas con este método junto con el usado en el ejercicio anterior.
-
Escriba un programa para trazar la siguiente ecuación:
f(x) = 4 / π * [ ∑( sen(nx) / n ) ],n = 1,3,5,7,..., +∞ (infinito).
Si escribimos unos cuantos términos de la suma, obtenemos lo siguiente:
f(x) = 4 / π * [sen(x) +sen(3x) / 3 +sen(5x) / 5 +sen(7x) / 7 +sen(9x) / 9 +sen(11x) / 11 +sen(13x) / 13 + ...]
Restricciones:x = [-2π, +2π], y = [-1,5, +1,5],
Resolución: 800 x 800,
Como no podemos llegar hasta +infinito, entonces elegiremos un intervalo finito. Esto es,n := [1,N]
-
N = 3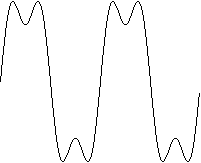
Ejercicio 3a -
N = 7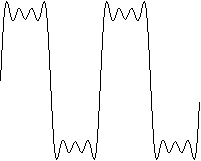
Ejercicio 3b -
N = 21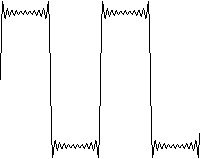
Ejercicio 3c
Observaciones: Cuanto mayor sea el valor de N, obtendremos una mayor precisión de la ecuación. Esto implica que nuestro error se reducirá a 0 (cero) o al menos a un valor insignificante. -
-
La ecuación presentada en el ejercicio #3 es, en realidad, la serie de Fourier para esta ecuación periódica:
Si-π < x < 0,f(x) = -1.0 < x < +∞,f(x) = 1.
Reescriba el programa del ejercicio anterior #3 - usando las mismas restricciones y resolución - para dibujar la función anterior, presentada en este ejercicio #4. Si sabe manipular colores, use distintos colores para cada trazado. Si no puede distinguir un trazado del otro, entonces cree otro programa diferente y ejecute ambos simultáneamente. Compare ambos trazados. Después de varias sumas (por ejemplo, N = 21), el trazado de la serie de Fourier (ejercicio #3) se parecerá o igualará al de esta ecuación (ejercicio #4).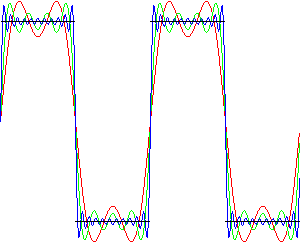
Ejercicio 4
Observaciones: 1) La función no define algunos valores def(x)para todos los valores dex. El dominio (valores dex) es el intervalo (-π, 0) ∪ (0, +π), ∪ significa unión. Los valoresx1 = -π,x2 = 0,x3 = +πf(x).
2) La ecuación anterior debe ser trazada periódicamente. Es decir, el mismo trazado debe ser igual para los intervalosx := ... ∪(-3π, -2π) ∪(-2π, -π) ∪(-π, 0) ∪(0, +π) ∪(+π, 2π) ∪(+2π, +3π) ∪ ... -
Otra forma de crear curvas es basándonos en un parámetro común para
xey. Esto sería,x = x(t)ey = y(t), dondetes nuestro parámetro. Tales ecuaciones están en forma paramétrica. Escriba un programa para trazar las siguientes curvas paramétricas:-
x(t) = sen(t), y(t)= cos(t), 0 ≤ t ≤ 2π, 
Ejercicio 5a -
x(t) = t*cos(t), y(t) = 3t*sen(t), 0 ≤ t ≤ 8π, 
Ejercicio 5b -
x(t) = (1 - t2) / (1 + t2), y(t) = 2t / (1 + t2), -π ≤ t ≤ +π, 
Ejercicio 5c -
x(t) = a*cos(t) + b*cos(at/2), y(t) = a*sen(t) - b*sen(at/2), 0 ≤ t ≤ 2π,
-
a = 8, b = 5
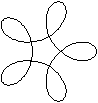
Ejercicio 5d1 -
a = 6, b = 5
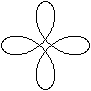
Ejercicio 5d2 -
a = 6, b = 2
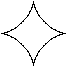
Ejercicio 5d3 -
a = 12, b = 8
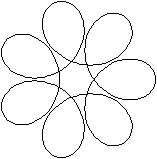
Ejercicio 5d4 -
a = 14, b = 8,6
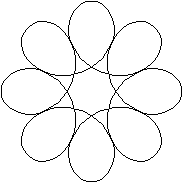
Ejercicio 5d5
-
Observaciones: Al usar ecuaciones paramétricas, el parámetro t sirve
para calcular la pareja de valores
delta_t = |tf - ti| / n,
donde