Apéndice 1: Geometría

Daremos un repaso general de la geometría, haciendo hincapié en la trigonometría.

Definiciones

Triángulo: Polígono cerrado de tres ángulos, y por tanto con tres lados.

• Rectángulo: Triángulo que tiene un ángulo recto; o sea, de 90°. Cada lado que forma el ángulo de 90° se llama cateto y el lado, que une los catetos, se llama hipotenusa. La hipotenusa es siempre mayor que cualquiera de los dos catetos.
• Isósceles: Triángulo que tiene dos lados de igual longitud y por tanto, dos de los ángulos son iguales.
• Equilátero: Triángulo que tiene los tres lados de igual longitud al igual que sus tres ángulos: 60°.

Cuadrilátero: Polígono cerrado de cuatro lados.

• Paralelogramo: Un cuadrilátero cuyos lados opuestos son paralelos y de igual longitud.
• Rombo: Un paralelogramo cuyos lados son de igual longitud.
• Rectángulo: Un paralelogramo cuyos lados forman ángulos rectos (90°).
• Cuadrado: Un rectángulo cuyos lados miden la misma longitud.

Geometría General

Líneas Rectas

Ecuaciones

Ecuaciones para una línea recta:

y-y0 = m (x-x0),

Esta ecuación describe una línea recta que pasa por el punto (x₀, y₀), con una pendiente m. Resolviendo para y, obtenemos la siguiente ecuación:

y = m x + b,

En esta ecuación, se describe una línea recta, con una pendiente m, que corta el eje Y (la ordenada) en el punto (0, b), y corta el eje X (la abscisa) en el punto (-b/m, 0).

Si x es una constante, x_c, entonces nuestra ecuación describe una línea recta vertical:

x = xc,

Si y es una constante, y_c, entonces nuestra ecuación describe una línea recta horizontal:

y = yc

Propiedades entre dos líneas rectas

Dos líneas rectas son coincidentes, cuando una línea sobrepone a la otra. Dicho de otro modo, todos los puntos de ambas líneas son comunes entre sí.

Dos líneas rectas son paralelas, cuando una línea no cruza la otra. Dicho de otro modo, no existe un punto común para ambas líneas.

Dos líneas rectas son perpendiculares, cuando una línea corta la otra formando un ángulo recto (90°).

Dos líneas rectas son oblicuas, cuando las líneas que intersectan no son perpendiculares.

Trigonometría

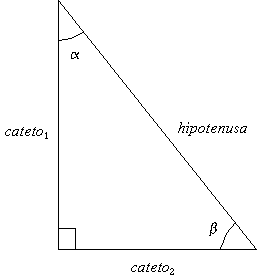
Para un triángulo rectángulo, se establecen las siguientes fórmulas:

hipotenusa2 = (cateto1)2 + (cateto2)2  (Teorema de Pitágoras)

         cateto opuesto
sen x = ----------------
           hipotenusa

         cateto contiguo
cos x = -----------------
           hipotenusa

         cateto opuesto
tg x  = -----------------
         cateto contiguo

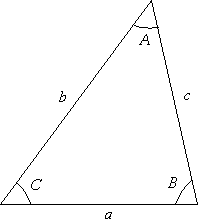
Sean a, b, y c las longitudes de cada lado de un triángulo arbitrario y sean A, B, y C los ángulos opuestos a los lados mencionados respectivamente, se establecen las siguientes fórmulas:

c2 = a2 + b2 - 2 a b cos C    (Ley de cosenos)

 sen A     sen B     sen C
------- = ------- = -------  (Ley de senos)
   a         b         c

sen(-x) = -sen x

cos(-x) = cos x

       sen x
tg x = -------
       cos x

          1
cosec x = -------
          sen x

        1
sec x = -------
         cos x

	   1       cos x
cotg x = ------- = -------
          tg x     sen x

sen2 x + cos2 x = 1

tg2 x + 1 = sec2 x

1 + cotg2 x = cosec2 x

sen(x+y) = sen(x) cos(y) + cos(x) sen(y)

cos(x+y) = cos(x) cos(y) - sen(x) sen(y)

          tg x + tg y
tg(x+y) = -------------------
           1 - tg(x) tg(y)

sen 2x = 2 sen(x) cos(x)

cos 2x = cos2 x - sen2 x

sen2(x/2) = (1 - cos x) / 2

cos2(x/2) = (1 + cos x) / 2