Apéndice 2: Vectores
Los vectores sirven para agrupar valores numéricos ordenados linealmente. Los vectores tienen ciertas propiedades matemáticas que pueden resultar en cálculos más rápidos. Para la teoría de gráficos, usamos vectores en la representación de ciertos objetos y conceptos descritos por su orientación - vector - y un punto - localización. Generalmente, usaremos vectores de 4 elementos, para describir la orientación de ejes de un sistema de coordenadas o incluso la orientación de la cámara de una escena, por ejemplo.
Definiciones
Un vector es un conjunto de elementos que geométricamente describe un segmento orientado. Este segmento conlleva suficiente información para conocer la orientación, dirección, y su magnitud (o longitud). Visto de otra manera:
v = ( v1, v2, v3, v4, …, vn )
Aquí v es un vector de dimensión (u orden) n, ya que tiene n elementos o componentes.
Para obtener un vector, requerimos dos puntos, ya que un vector es al fin y al cabo un segmento. Las coordenadas de ambos puntos se restan para calcular el vector. Esto es, tenemos los dos siguientes puntos:
A = ( a1, a2, a3, a4, …, an ) B = ( b1, b2, b3, b4, …, bn )
Para conseguir un vector desde el punto A al punto B, realizamos la siguiente operación:
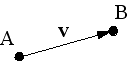
v = B-A = ( b1-a1, b2-a2, b3-a3, b4-a4, …, bn-an )
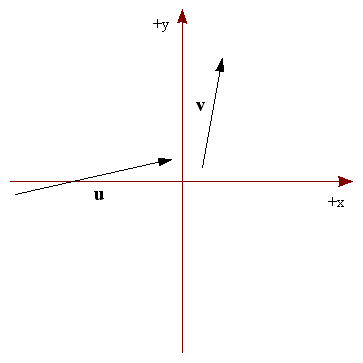
Podemos ver el resultado gráficamente en la Figura 1:
Orientación
También obtendremos un vector desde B hasta a A. Sin embargo, la orientación o el sentido del vector w es contraria a la del vector v. El vector se obtendría de esta manera:
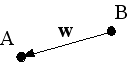
w = A-B = ( a1-b1, a2-b2, a3-b3, a4-b4, …, an-bn )
Podemos comparar gráficamente la diferencia de cada vector viendo la Figura 2:
Por lo tanto, tenemos que,
w = -v
El signo negativo para vectores significa que el vector tiene una orientación o sentido contrario.
Pendiente
Un vector tiene dirección que es lo mismo que la pendiente. Como un vector contiene la diferencia entre las coordenadas de dos puntos, entonces podemos calcular fácilmente la pendiente.Usamos la siguiente fórmula para vectores en 2D:
v = ( v1, v2 ) m = v2 / v2
Módulo
Un vector también tiene longitud o magnitud, llamado módulo del vector. Ésta se calcula de la siguiente manera usando el teorema de Pitágoras:
v = ( v1, v2, v3, v4, …, vn ) ‖v‖2 = (v1)2 + (v2)2 + (v3)2 + (v4)2 + … + (vn)2
Si un vector tiene como módulo 1, entonces se trata de un vector unitario.
Vector Nulo
Hay que hacer mención del vector cero, 0, el cual se define así:
0 = ( 0, 0, 0, …, 0 )
Este vector simplemente no tiene ni dirección, ni por tanto orientación, pero tiene magnitud 0 (cero). Por estas razones, se le suele llamar el vector nulo.
Equivalencia
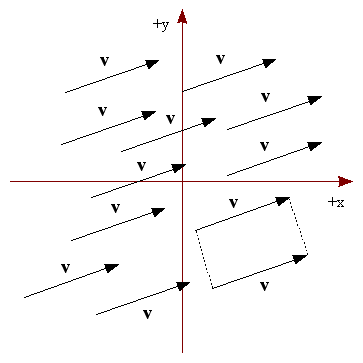
Dos vectores son iguales si sus componentes homólogos son iguales. Expresamos este concepto de esta manera:
u = ( u1, u2, u3, u4, …, un ) v = ( v1, v2, v3, v4, …, vn ) u = v si y sólo si, u1 = v1 u2 = v2 u3 = v3 u4 = v4 ⋮ un = vn
Los vectores iguales entre sí tienen la misma dirección, orientación, y magnitud. Esto implica que los vectores son paralelos entre sí. Esto se puede apreciar geométricamente en la Figura 3.
Ejemplos
Veamos algunos ejemplos.
Ejemplo 1
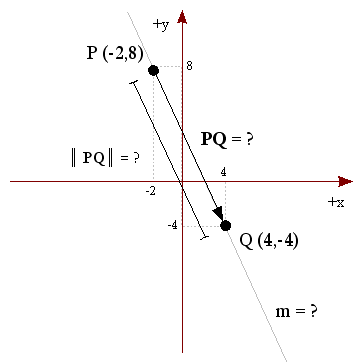
Calcule el vector PQ, su módulo, y la pendiente m a partir de estos dos puntos:
P = ( -2, 8 ) yQ = ( 4, -4 )
Solución
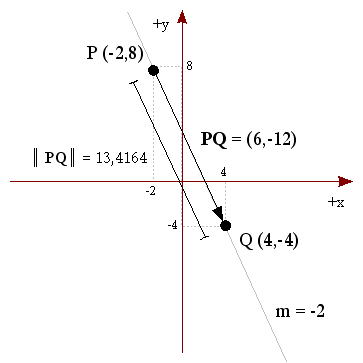
Calculamos el vector PQ,
PQ = Q-P =( 4, -4 ) - ( -2, 8 ) =( 4-(-2), -4-8 ) =( 6, -12 )
La pendiente m es:
m = -12 / 6 = -2
El módulo del vector v es:
‖PQ‖ =√( 62 + (-12)2 ) =√( 36 + 144 ) =√ 180 ≅ 13,4164
Ejemplo 2
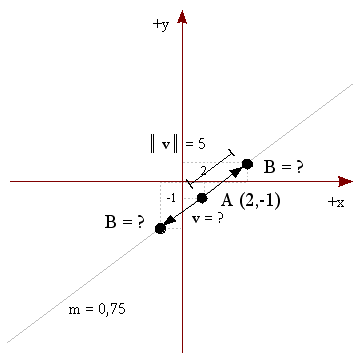
Determine las coordenadas del punto B, dada la siguiente información:
- El punto A = ( 2, -1 ) y B pertenecen a la misma línea recta
- La pendiente de tal línea es m = 0,75
- El punto B se encuentra en el tercer cuadrante y a 5 unidades del punto A
Solución
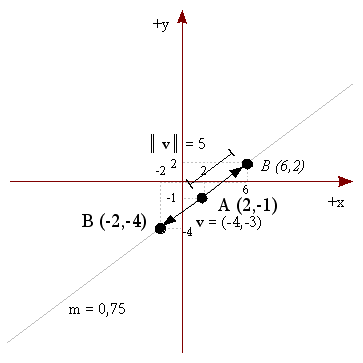
Vamos a intentar calcular el vector AB, para ver hasta dónde podemos llegar y así ver qué información nos hace falta.
v = AB = B-A =( x, y ) - ( 2, -1 ) =( x-2, y+1 )
O sea, tenemos lo siguiente:
v = ( vx, vy ) = ( x-2, y+1 ),
esto implica que,
vx = x-2 vy = y+1
Obviamente, necesitamos determinar los valores de x e y que forman las coordenadas del punto B.
Como nos dan la pendiente m, usaremos su fórmula:
m =vy / vx ⇒0,75 = vy / vx ⇒vy = 0,75 vx
También nos dan la distancia entre ambos puntos: 5. La distancia es en realidad el módulo del vector v, la cual conocemos su fórmula:
‖v‖2 = (vx)2 + (vy)2
Con la información dada, tenemos que,
52 = (vx)2 + (vy)2
Sustituimos los componentes del vector v con la ecuación que obtuvimos - basada en la pendiente. Esto es,
25 =(vx)2 + (0,75 vx)2 ⇒25 = (vx)2 + 0,5625 (vx)2 ⇒25 = 1,5625 (vx)2 ⇒√16 = vx ⇒vx = 4
Volvemos a la ecuación de la pendiente para averiguar vy,
vy = 0,75 vx = 0,75*4 = 3
Ahora, sustituimos los componentes del vector v en las primeras ecuaciones que obtuvimos. Esto es,
vx = x-6 ⇒ 4 = x-2 ⇒ x = 6 vy = y-3 ⇒ 3 = y+1 ⇒ y = 2
Por lo tanto, el punto B = ( 6, 2 ). No obstante, se nos olvida el último dato importante: el punto B se encuentra en el tercer cuadrante. Revisando las coordenadas que hemos calculado, vemos que el punto ( 6, 2 ) pertenece al primer cuadrante y no al tercero. Recordamos, que un vector tiene orientación y por tanto es posible que estemos ante un vector con un sentido contrario al que pensábamos. Esto es posible ya que calculamos la pendiente basándonos en que los componentes del vector eran ambos positivos, pero también puede darse el caso de que ambos sean negativos. Esto es,
m =-vy / -vx ⇒0,75 = -vy / -vx
Por consiguiente, tenemos que,
v = ( -4, -3 )
Esto implica que,
vx = x-2 ⇒ -4 = x-2 ⇒ x = -2 vy = y+1 ⇒ -3 = y+1 ⇒ y = -4
Consecuentemente, nuestro punto B = ( -2, -4 ) es el que se nos pide ya que yace en el tercer cuadrante.
Operaciones de Vectores
Existen cuatro operaciones de vectores básicas: multiplicación escalar-vector, suma vector-vector, resta vector-vector, producto escalar, y producto vectorial.
Multiplicación Escalar-Vector
Es la multiplicación del escalar s por cada elemento del vector v.
sv = s * ( v1, v2, v3, v4, …, vn ) = ( sv1, sv2, sv3, sv4, …, svn )
Este tipo de multiplicación tiene las siguientes propiedades:
- conmutativa: sv = vs
- asociativa: s(tv) = (st)v
- distributiva: (s+t)v = sv + tv
Como el escalar s modifica todos los elementos de un vector igualmente, entonces el vector en sí cambia proporcionalmente. Esto implica que la dirección no varía, pero posiblemente sí su orientación y magnitud. Veamos los casos:
| Condición | Efecto | Ejemplo |
| Si s > 1 | el módulo de v aumenta |
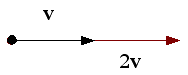
|
| Si s = 1 | v no varía y por tanto, su módulo tampoco |
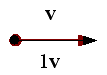
|
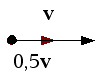
| Si 0 < s < 1 | el módulo de v disminuye |
|
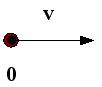
| Si s = 0 | v = 0 y por tanto, su módulo es 0 |
|
| Si s < 0 | el módulo de v varía según la cantidad de s, pero su signo hace invertir la orientación o sentido del vector v |
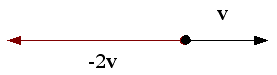
|
Suma Vector-Vector
Se suman los elementos correspondientes de los dos vectores. La suma sólo se puede hacer si los dos vectores son del mismo orden o dimensión: el número de elementos es el mismo para el vector u y v:
u + v =( u1, u2, u3, u4, …, un ) + ( v1, v2, v3, v4, …, vn ) =( u1+v1, u2+v2, u3+v3, u4+v4, …, un+vn )
La suma de vectores acepta las propiedades:
- conmutativa:
u + v = v + u - asociativa:
u + (v + w) = (u + v) + w - distributiva (con escalares):
s(u + v) = su + sv
Por supuesto, todos los vectores han de ser de orden n.
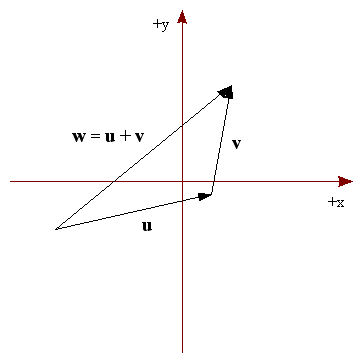
Geométricamente, el resultado de la suma de vectores es otro vector llamado el vector resultante. Como los vectores no están fijados a un punto, podemos "mudarlos" a nuestro antojo. Si colocamos uno de los vectores para poder encadenarlo a nuestro otro vector sumando, observamos que el resultante forma un triángulo junto con los otros dos sumandos. La forma de encadenar los vectores es colocando la cola de un vector sobre la cabeza de otro. Esto se puede comprobar en las Figura 13 y Figura 14.
Resta Vector-Vector
Se restan los elementos correspondientes de los dos vectores. Como en la suma, la resta de dos vectores sólo es posible si ambos son del mismo orden. Esto es,
u - v =( u1, u2, u3, u4, …, un ) - ( v1, v2, v3, v4, …, vn ) =( u1-v1, u2-v2, u3-v3, u4-v4, …, un-vn )
La resta entre vectores realmente es la suma del minuendo y el sustraendo en forma negativa. Esto es,
u - v =u + (-v)
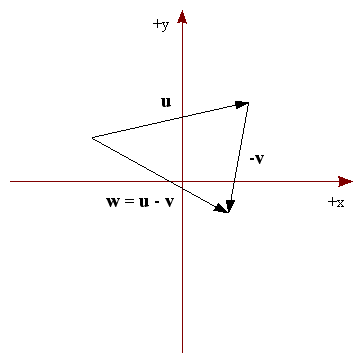
Analizando esta operación a través de la geometría, vemos que implementamos la misma técnica de encadenar los vectores. Sin embargo, al tratarse de una suma pero con el vector sustraendo en el sentido contrario, encadenamos este vector negativo. Esto se puede ver mejor en la Figura 15.
Producto Escalar
Esta operación nos da como resultado un escalar que tiene relación con la magnitud de un vector resultante de dos vectores. El producto escalar se realiza multiplicando los componentes homólogos de ambos vectores y luego sumando tales productos. Por lo tanto, si tenemos que,
u = ( u1, u2, u3, u4, …, un ) v = ( v1, v2, v3, v4, …, vn )
entonces su producto escalar es,
u⋅v = u1v1 + u2v2 + u3v3 + u4v4 + … + unvn
El producto escalar tiene las siguientes propiedades:
u⋅u = ‖u‖2
u⋅v = v⋅u
u⋅( v+w ) = u⋅v + u⋅w
(su)⋅v = s(u⋅v) = u⋅(sv)
Si α es el ángulo entre dos vectores, u y v, entonces tenemos que,
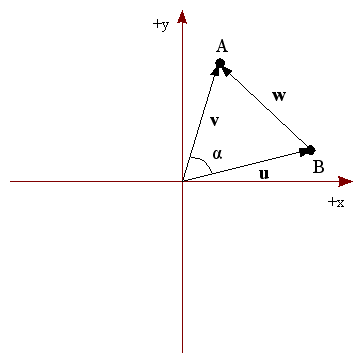
u⋅v = ‖u‖ ‖v‖ cos α
Esto implica que existe una relación entre el ángulo α y el producto escalar. Con ambas fórmulas, podemos descubrir el ángulo α entre dos vectores. Esto se ve claramente en la Figura 16.
Podemos deducir los siguientes casos:
-
u⋅v = 0 implica que el ángulo α = α/2 (90°) y por tanto, u y v son perpendiculares. Se dice que u y v son ortogonales. Si, además de ser ortogonales, u y v son vectores unitarios (de módulo 1), entonces decimos que los vectores son ortonormales.
-
Si el ángulo α = 0 (0°) ó α = π (180°), entonces u y v son paralelos
Aplicando la ley de cosenos, para triángulos,
c2 = a2 + b2 - 2 a b cos α
observamos la siguiente fórmula:
‖w‖2 = ‖u‖2 + ‖v‖2 - 2 ‖u‖ ‖v‖ cos α
Esto implica que,
‖w‖2 = ‖u‖2 + ‖v‖2 - 2 u⋅v
Producto Vectorial
Esta operación sirve para determinar un nuevo vector que es perpendicular - ortogonal - a ambos vectores operandos. Dados dos vectores no paralelos, u y v, en un espacio tridimensional, el producto vectorial dará un tercer vector, w, que es ortogonal a ambos. Debemos tener:
w ⋅ u = w ⋅ v = 0
Tenemos dos vectores de tres elementos, u y v, definidos de la siguiente manera:
u = ( u1, u2, u3 ) v = ( v1, v2, v3 )
Definimos el vector w como el determinante con estos elementos:
| i j k |
w = u × v = | u1 u2 u3 | = (u2v3 - u3v2)i - (u1v3 - u3v1)j + (u1v2 - u2v1)k
| v1 v2 v3 |
Aquí i, j, y k representan los vectores unitarios: (1, 0, 0), (0, 1, 0), y (0, 0, 1), respectivamente. Observamos que i es el vector con la misma dirección que el eje X, con el sentido positivo, y tiene como longitud 1. Lo mismo ocurre con los vectores j y k.
Podemos reescribir el resultado del determinante, que es el vector w:
w = ( u2v3 - u3v2, u1v3 - u3v1, u1v2 - u2v1 )
El producto vectorial tiene las siguientes propiedades:
-
u × u = u × 0 = 0 × u = 0
-
u × v = - ( v × u )
-
u × ( v + w ) = ( u × v ) + ( u × w )
-
u ⋅ ( v × w ) = ( u × v ) ⋅ w
-
u × ( v × w ) = ( u ⋅ w ) v - ( u ⋅ v ) w
-
( su ) × v = u × ( sv ) = s ( u × v ),
donde s es un número real: un escalar.
-
‖u × v‖2 = ‖u‖2 ‖v‖2 - (u ⋅ v)2
Como se puede apreciar en la primera propiedad, el orden de los operandos para el producto vectorial influye en el vector resultante. Sin embargo, la única diferencia entre los dos posibles vectores, es un cambio de sentido; es decir:
u × v = - ( v × u )
Existe otra propiedad con el módulo del producto vectorial:
‖u × v‖ = ‖u‖ * ‖v‖ * sen α,
donde α es el ángulo formado entre los vectores u y v.
Dicho lo anterior, podemos deducir los siguientes casos:
-
u × v = 0
implica que el ángulo α = 0 (0°) ó α = π (180°) y por tanto, u y v son paralelos.
-
Si el ángulo α = π/2 (90°), entonces u y v son perpendiculares.
Ejemplos
Dados los vectores: u = ( -3, 5, 1 ) y v = ( 4, -2, -1 ), determine el producto vectorial tanto de u × v como de v × u, y el ángulo entre ambos vectores, usando el módulo del producto vectorial.
| i j k |
w = u × v = | -3 5 1 |
| 4 -2 -1 |
= (5*(-1) - 1*(-2))i - ((-3)*(-1) - 1*4)j + ((-3)*(-2) - 5*4)k
= -3i + j - 14k
| i j k |
w′ = v × u = | 4 -2 -1 |
| -3 5 1 |
= ((-2)*1 - (-1)*5)i - (4*1 - (-1)*(-3))j + (4*5 - (-2)*(-3))k
= 3i - j + 14k
Como podemos observar w = -w′, por lo que ‖w‖ = ‖w′‖ :
‖w‖ = √( (-3)2 + (1)2 + (-14)2 ) = √206 = 14,3527 unidades
Ahora podemos averiguar el ángulo α que forman estos dos vectores:
‖u‖ = √( (-3)2 + (5)2 + (1)2 ) = √35 = 5,9161 unidades
‖v‖ = √( (4)2 + (-1)2 + (-1)2 ) = √18 = 4,2426 unidades
‖u × v‖ 14,3527
sen α = -------- = ----------------- = 0,5718
‖u‖ ‖v‖ 5,9161 * 4,2426
α = sen-1 0,5718 = 0,6087 radianes ⇒ 34,88º
Otras Operaciones
Aquí presentamos otras cuatro operaciones asociadas a vectores.
Combinación Lineal
Se trata de obtener un vector a partir de una combinación de otros n vectores u1, u2, u3, u4, …, un y un conjunto de n escalares a1, a2, a3, a4, …, an. Esto es,
u = a1u1 + a2u2 + a3u3 + a4u4 + … + anun
Si el único conjunto de escalares tal que,
a1u1 + a2u2 + a3u3 + a4u4 + … + anun = 0
es
a1 = a2 = a3 = a4 = … = an
entonces se dice que estos vectores son linealmente independientes. Dicho de otra manera, si u no puede ser representado usando una combinación lineal de otros vectores, entonces son linealmente independientes.
La mayor cantidad de vectores linealmente independientes que podemos encontrar para un espacio indica la dimensión de ese espacio. Por ejemplo, si tenemos tres vectores linealmente independientes entre sí, entonces ese espacio es tridimensional, ya que todos los vectores en ese espacio pueden ser representados por estos tres vectores linealmente independientes.
Base de vectores
Si un espacio vectorial tiene n dimensiones, entonces cualquier conjunto de n vectores linealmente independientes forma una base. Típicamente usamos una base de vectores para describir un sistema de coordenadas si estos vectores son perpendiculares entre sí. Esto implica que tales vectores y la base son ortogonales.
Digamos que tenemos el conjunto de vectores v1, v2, v3, v4, …, vn que forma una base de vectores. Podemos representar cualquier vector v únicamente como una combinación lineal de esta base de vectores. Esto es,
v = b1v1 + b2v2 + b3v3 + b4v4 + … + bnvn
donde b1, b2, b3, b4, …, bn son escalares.
En la práctica, escribimos los vectores unitarios que forman la base del plano cartesiano así:
i y j para ℝ2, e i y j para ℝ3
Nota: Los ingenieros escriben tales vectores con un circunflejo: î, ĵ, y k̂.
Proyección
La proyección nos ayuda para determinar la longitud (escalar) de la proyección perpendicular de un vector a sobre la línea recta determinada por un vector b. También podemos hablar del componente de a sobre b como la proyección. Esto se puede calcular geométricamente de esta manera:
compb a = ‖a‖ cos α
La expresión a la derecha del símbolo de igualdad se parece mucho a la definición del producto escalar. Por lo tanto, podemos reescribir la fórmula anterior de esta manera:
‖a‖ ‖b‖ cos α a⋅b
compb a = ------------- = -----
‖b‖ ‖b‖
El resultado es positivo si el ángulo 0 < α < π/2 y negativo si α > π/2.
Ya que la proyección nos da la longitud de la proyección, podemos averiguar los vectores componentes de a sobre b. Esto es, podemos averiguar los vectores paralelo,
b
a‖ = (compb a) ---
‖b‖
a⊥ = a - a‖
Ejemplos
Algunos ejemplos acerca de estas operaciones son:
Ejemplo 1
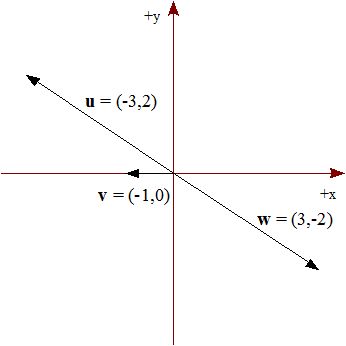
Dados los siguientes vectores:
u = ( -3, 2 ) v = ( -1, 0 ) w = ( 3, -2 )
- Determine cuáles de estos vectores son linealmente independientes entre ellos.
- Averigüe cuáles de estos vectores forman una base.
- Represente el vector que no es linealmente independiente y que no forma una base en términos de la base averiguada del apartado b).
Solución
-
Comprobamos la combinación lineal de cada pareja de vectores por independencia lineal.
Veamos la pareja u y v,
0 = a u + b v; ( 0, 0 ) = a ( -3, 2 ) + b ( -1, 0 ) = ( -3a-b, 2a )
Por lo que tenemos,
0 = -3a-b 0 = 2a ⇒ a = 0 ⇒ b = 0
Concluimos que u y v son linealmente independientes.
Ahora comprobamos la pareja u y w,
0 = a u + b w; ( 0, 0 ) = a ( -3, 2 ) + b ( 3, -2 ) = ( -3a+3b, 2a-2b )
Por lo que tenemos,
0 = -3a+3b 0 = 2a-2b
Esto implica que, a = b y por tanto, no existe una única solución.
Estos dos vectores son linealmente dependientes.
Por último, revisemos la pareja v y w,
0 = a v + b w; ( 0, 0 ) = a ( -1, 0 ) + b ( 3, -2 ) = ( -a+3b, -2b )
Por lo que tenemos,
0 = -a+3b ⇒ a = 0 0 = -2b ⇒ b = 0
Concluimos que v y w son linealmente independientes.
Podemos formar dos bases:
- u y v, y
- v y w
- Escribimos cada vector que no pertence a la base como una combinación lineal de los otros dos vectores,
-
Con la base, u y v, representamos w de la siguiente manera,
w = a u + b v; ( 3, -2 ) = a ( -3, 2 ) + b ( -1, 0 ) = ( -3a-b, 2a )
Por lo que tenemos,
3 = -3a-b -2 = 2a ⇒ a = -1 y por tanto b = 0
Es decir,
w = -u
-
Usando la base, v y w, representamos u así,
u = a v + b w; ( -3, 2 ) = a ( -1, 0 ) + b ( 3, -2 ) = ( -a+3b, -2b )
Por lo que tenemos,
3 = -a+3b 2 = -2b ⇒ b = -1 y por tanto a = 0
Al final, obtenemos que,
u = -w
-
Ejemplo 2
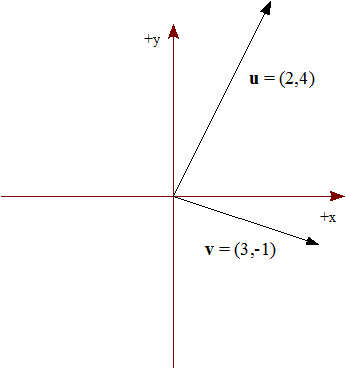
Dado el vector
Solución
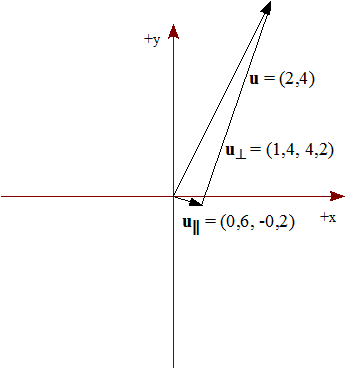
Calculemos el componente paralelo de u,
(2,4)⋅(3,-1) 6-4
compv u = ------------ = ----- = 0,6325
‖v‖ √10
Obtenemos los siguientes vectores,
u‖ =0,6325*(3,-1) / √10 =(3/5,-1/5) =(0,6, -0,2) u⊥ =u - u‖ =(2,4) - (0,6, -0,2) =(1,4, 4,2)