Capítulo 4 - Nubes

En este capítulo, veremos la forma de generar nubes blancas con un fondo de un cielo azul. Esto lo haremos manipulando los píxeles y los colores, según unas fórmulas sencillas. Por lo tanto, daremos una breve explicación acerca de los colores, antes de dar paso a la explicación y al algoritmo para crear nubes.

Colores

En el capítulo 1, se dio una breve explicación de los colores y los modelos de colores. En nuestra discusión de programación de gráficos, usaremos el modelo RGB. Intentamos modelar la luz descomponiéndola en tres colores primarios; también llamados estímulos tricolores. Sumando los tres estímulos, obtendremos un color o, mejor dicho, un tono de un color determinado. En sistemas gráficos, como ordenadores, cada estímulo o intensidad de un tricolor es representado por un valor numérico entero no negativo, que es limitado por una cantidad de bits. Dependiendo de la cantidad de bits, podremos usar más o menos colores a nuestra disposición. En este tema, al referirnos a varios miles de colores, realmente nos referimos a varios tonos de ciertos colores. Sin embargo, como el ordenador se basa en valores numéricos, cada número y, por tanto, cada combinación de números es diferente. Esto implica que los colores y tonos de colores representados por tales números son también diferentes colores, desde el punto de "vista" del ordenador o sistema gráfico.

Por ejemplo, con una cantidad de 15 bits para guardar la información de cada color, nos ofrece una gama de 2¹⁵ = 32.768 colores diferentes. De igual forma, una cantidad de 24 bits para crear un color, obtendremos una cantidad de 2²⁴ = 16.777.216 colores diferentes. Esta cantidad de bits para cada color se denomina profundidad de colores, del inglés colour depth. Como cada píxel puede tener un color diferente, se suele hablar de las prestaciones de un sistema gráfico al hablar de bits por píxel, o simplemente bpp.

Al hablar de 15 bpp, estamos tratando un sistema gráfico con una gama total de 32.768 colores y por tanto, cada píxel contiene 15 bits para describir su color correspondiente. Si la imagen a mostrar es de dimensión, 500 x 500, entonces dicha imagen tiene un tamaño de 500 × 500 × 15 = 3.750.000 de bits que equivale a 468.750 bytes que son unos 458 KB aproximadamente. Ahora bien, en memoria, se suele usar bytes enteros. Por lo tanto, no podemos tratar 15 bits, pero sí 16 bits, ya que son 2 bytes enteros. Recalculando lo anterior con 16 bpp, obtenemos que, nuestra imagen es de unos 488 KB, aproximadamente. Esta profundidad de colores se suele llamar "color [de nivel] alto" del inglés "high colour"; productos estadounidenses lo escriben como "hicolor". Con una imagen de 500 x 500 á 24 bpp, obtenemos un tamaño de unos 732 KB. Una profundidad de 24 bpp se llama "color auténtico", del inglés "true colour", ya que se usa como base para mostrar imágenes fotorrealistas.

Modelo RGB

Vamos a tratar el modelo RGB con una profundidad de 24 bpp. Por lo tanto, cada intensidad - rojo, verde, y azul - es controlada por valores numéricos de 8 bits por cada intensidad. Visto de otra forma, las intensidades de rojo, verde, y azul tienen un intervalo de 0 á 255 (ambos incluidos), cada una. Un valor de 0 indica la intensidad mínima; o sea, el color está "apagado". Un valor de 255 indica una intensidad máxima.

Combinando valores para cada intensidad, podemos recrear la mayoría de los colores visibles. Por ejemplo,

Rojo = 255, Verde = 0, Azul = 0,

Obtenemos el color rojo, ya que la intensidad del rojo es máxima, y las otras son mínimas (apagadas).

Otro ejemplo,

R=127, V=127, A=127,

Obtendremos un color gris, ya que todas las intensidades son iguales y a la mitad del intervalo. Por consiguiente, el color negro es:

R=0, V=0, A=0,

y el color blanco es:

R=255, V=255, A=255

Algunos sistemas y librerías gráficas, usan porcentajes en lugar de valores enteros. Esto es para no tener que definir los colores con acorde a la profundidad. Al usar valores numéricos, tendremos un problema si queremos cambiar la profundidad, o incluso si el sistema gráfico no alcanza la profundidad establecida por el programa o por la imagen. Algunos sistemas gráficos aplicarán una fórmula para averiguar un color aproximado al requerido. Si usamos un valor decimal a modo de porcentaje, entonces no tendremos muchos problemas de compatiblidad entre diferentes profundidades, pero consecuentemente se tendrá que convertir los porcentajes a valores numéricos siempre. Esto supone un gasto añadido de tiempo al mostrar la imagen.

El uso de porcentajes describe cada color indirectamente, mientras que el uso de valores enteros, dentro del intervalo de bits, describe cada color directamente según la profundidad establecida.

Abajo podemos practicar combinando cada una de las intensidades - Rojo, Verde, y Azul - para formar un color.

Applet para Colores

Nota: Se requiere la máquina virtual de Sun (Sun VM) para poder ejecutar este applet de Java.

Paletas

Vamos a hablar de paletas de colores, pero no entraremos en mucho detalle. Los pintores suelen usar unos cuantos colores básicos para dibujar sus cuadros. Tales colores se colocan en una paleta. Luego, se mezclan los colores básicos en la misma paleta para crear otros tonos y mezclas. El tema de gráficos generados por computación se sirve de este concepto de una paleta.

En algunos sistemas gráficos, especialmente antiguos, en lugar de manipular los colores directamente con el modelo RGB, se usaban números enteros a modo de índices. Previamente, se establecía todos los colores que se iban a usar para una imagen o programa. Básicamente, se crean los colores y se guardan en una lista. Al usar funciones gráficas, los píxeles contienen índices que indirectamente hacen referencia a esta lista o tabla donde se guardan los colores. Siguiendo el ejemplo en el apartado anterior: 500 x 500 x 16, digamos que tenemos una paleta de 8 bits. Esto supone que tenemos una paleta de 256 colores y por tanto 256 valores a modo de índices. Para cada píxel, sólo guardamos el índice del color y no el color en sí. Por lo tanto, 500 × 500 × 8 = 2.000.000 bits = 250.000 bytes, que es aproximadamente, 244 KB. Por supuesto, tenemos que agregar la paleta de 256 colores × 16 bpp = 4.096 bits = 512 bytes. Al final, la imagen ocupará aproximadamente unos 245 KB. Comparando este tamaño con el de la imagen usando colores directamente, 488 KB, vemos que podemos ahorrarnos una cantidad de espacio considerable.

Generar Nubes

Ahora podemos dar paso a la explicación para generar nubes. Lo que hacemos es elegir un color aleatoriamente para cada uno de los 4 puntos que están en las 4 esquinas de nuestra imagen rectangular:

(x_i, y_i), (x_i, y_f), (x_f, y_i), y (x_f, y_f)

La figura 1 muestra los 4 puntos en las esquinas de nuestra imagen rectangular.

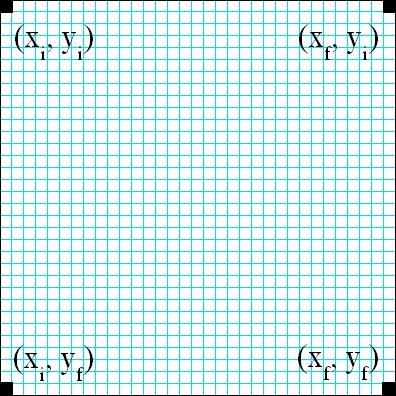
Luego, calcularemos un 5º punto, que se situará en el centro del rectángulo: (x′,y′) = ((x_i+x_f)/2, (y_i+y_f)/2), el cual contendrá la media de los colores de los 4 puntos (o esquinas) obtenidos previamente. Con las coordenadas de este 5º punto junto con las coordenadas de los 4 puntos de las esquinas, podemos calcular otros 4 puntos medios para cada lado de nuestra imagen rectangular:

(x′, y_i), (x_f, y′), (x′, y_f), y (x_i, y′)

La figura 2 muestra las nuevas coordenadas calculadas a partir de las 4 esquinas dadas:

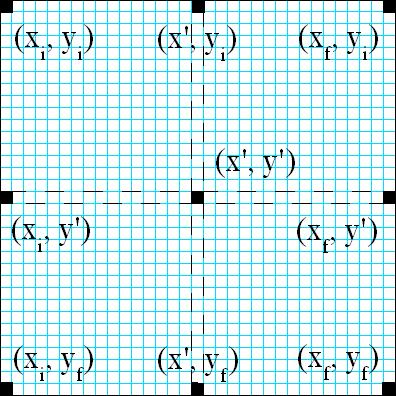
Para calcular el color de cada uno de estos puntos medios, calculamos la media de los colores de cada color de las 2 coordenadas de cada lado. Sin embargo, no obtendremos un resultado aleatorio, por lo que agregamos algo de aleatoriedad a la hora de calcular el nuevo color para el punto medio. El método de perturbación o aleatoriedad agregada se basa en la distancia entre las 2 coordenadas originales. Cuanto más distantes entre sí estén las coordenadas, mayor perturbación existirá. La idea es viceversa: cuanto menor sea la distancia entre las coordenadas, menor será el valor aleatorio. Esto resultará en agrupaciones de colores parecidos, cuanto menor sea la distancia, y por tanto, tendremos colores más dispares, cuanto más alejados estén las coordenadas entre sí. Para llevar a cabo este método de perturbación, el valor generado aleatoriamente será el parámetro para conseguir un color de nuestro mapa de colores; esto se explica más abajo.

Al tener 9 puntos: 4 esquinas, 4 puntos medios en cada lado, y 1 punto central, nuestra imagen rectangular puede divididirse en 4 rectángulos más pequeños. Recursivamente, repetimos el mismo proceso, aplicándolo a cada uno de los cuatro rectángulos o cuadrantes. Seguimos repitiendo tal proceso hasta que todos los píxeles de la imagen tengan asignados un color. Podemos ver la siguiente iteración en la figura 3, subdividiendo nuestra imagen rectangular en 4 áreas rectangulares para aplicar el mismo método a cada una:

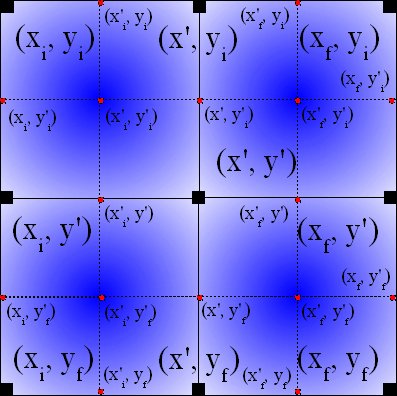
Al final del proceso, obtendremos una imagen parecida a la mostrada en la Figura 4:

Mapa de Colores

Para elegir un color aleatoriamente, necesitamos crear un mapa de colores. Tal mapa nos permitirá asociar un valor entero a un color determinado. Esto es parecido a una paleta, pero se generará el color elegido a partir de una fórmula. El procedimiento para realizar tal mapa de colores es algo sencillo. Basta con comprobar el intervalo del valor entero dado, y generar el color que queremos. Cada vez que queramos un color determinado, simplemente invocamos el mapa de colores para generarlo y obtenerlo. Por ejemplo,

Color Mapa( i )
1. Si i ≤ 0,10
   2. color ← de BLANCO (i=0,00) a AZUL (i=0,10)
3. Si 0,10 < i ≤ 0,50
   4. color ← de AZUL (i=0,10) a ROJO (i=0,50)
5. Si 0,50 < i
   6. color ← de ROJO (i=0,50) a AMARILLO (i=1,00)
7. Terminar( color )

El valor usado por el mapa de colores puede ser de cualquier intervalo. Podemos usar porcentajes como valores en el intervalo de [0, 255]. En el algoritmo anterior, obtenemos un color diferente según el porcentaje indicado por i. Por ejemplo, si queremos averiguar el color de i=0,75, podemos comprobar que se generará un color a mitad de camino entre el rojo y el amarillo, que será naranja, seguramente. Esto es porque 0,75 es la media entre 0,50 y 1,00. Usando el applet presentado anteriormente, conseguiremos un color anaranjado con R=255, V=127, A=0. Este color está a la mitad entre el color rojo: R=255, V=0, A=0 y el color amarillo: R=255, V=255, A=0. Calculando la media de cada intensidad: R=(255+255)/2, V=(0+255)/2, A=(0+0)/2, conseguimos nuestro color naranja: R=255, V=127, A=0.

Para obtener el cálculo anterior, tenemos que crear una fórmula basada en el valor de i. Tal fórmula puede ser:

6.1.  color.rojo  = 255
6.2.  color.verde = 255*(2*(i-0,50)) = 510*(i-0,50)
6.3.  color.azul  = 0

Cuando i valga 0,50, color.verde será 0 y cuando i valga 1,00, color.verde será 255. Esto es justamente lo que queremos, ya que podemos generar los demás colores comprendidos entre tales colores.

Algoritmo

El algoritmo se compone de varias funciones importantes:

Necesitamos la función principal, Generar_Nube(), que establecerá los valores iniciales y preparará el procedimiento adecuadamente.
La función Mapa() sirve para generar un color para las nubes a partir de un valor numérico entero no negativo en el intervalo [0, 255].
La función Subdividir() se encargará de la parte recursiva del algoritmo.
La función Generar_Parámetro() se encarga de obtener el color del punto medio de dos puntos. Se calcula la media de los colores de cada punto agregando un valor aleatorio. Como los colores nuevos deben pertenecer a nuestro mapa de colores, se basará el cálculo en los parámetros de los colores, en lugar de los colores verdaderos. Es decir, calcularemos el parámetro que representa el nuevo color. Luego, usaremos Mapa() para obtener el color verdadero según el parámetro.

Para Generar_Nube(), el algoritmo es:

Generar_Nube()Iniciar: valor_semilla, anchura_p, altura_p
Inicializar: parámetros[anchura_p, altura_p] ← -1 o cualquier valor negativo
Iniciar_Generador_Números_Aleatorios( valor_semilla )

// Obtener parámetros de colores
parámetros[0,0] ← Generar_Número(256)
parámetros[anchura_p-1,0] ← Generar_Número(256)
parámetros[anchura_p-1,altura_p-1] ← Generar_Número(256)
parámetros[0,altura_p-1] ← Generar_Número(256)

// Dibujar Esquinas
PonPíxel( 0,0, Mapa( parámetros[0,0] ) )
PonPíxel( anchura_p-1,0, Mapa( parámetros[anchura_p-1,0] ) )
PonPíxel( anchura_p-1,altura_p-1, Mapa( parámetros[anchura_p-1,altura_p-1] ) )
PonPíxel( 0,altura_p-1, Mapa( parámetros[0,altura_p-1] ) )

// Comenzar la Recursividad
Subdividir( parámetros, 0,0, anchura_p-1,altura_p-1 )
Terminar

La matriz o tabla parámetros, de dimensiones anchura_p x altura_p, guardará los parámetros usados para obtener un color del mapa, para cada píxel. Inicialmente, esta matriz contendrá valores negativos, que indican un estado inválido.
Las funciones Iniciar_Generador_Números_Aleatorios() y Generar_Número() representan funciones estándares que tiene el compilador para generar número aleatorios. La variable valor_semilla contiene el valor inicial para comenzar el generador de números pseudo-aleatorios. Usando un valor inicial conocido, podemos recrear la misma imagen con sólo usar el mismo número. De esta forma, asociamos un único valor con cada imagen generada. Para Generar_Número(N), se generará un número aleatoriamente en el intervalo [0, N-1].
La función PonPíxel() hace referencia a una función de la librería o API gráfica para establecer un color para un píxel determinado en la pantalla, según las coordenadas dadas.

Para Mapa(), el algoritmo es:

Color Mapa( x )color.rojo  ← |2*x-255|
color.verde ← |2*x-255|
color.azul  ← 255
Terminar( color )

color contiene los valores de cada estímulo del modelo RGB de 24 bpp. El mapa para crear nubes se basa en una gama de colores entre blanco, azul y de vuelta a blanco. Esto es, desde (255,255,255) pasando por (0,0,255) hasta llegar otra vez a (255,255,255). Por supuesto, podemos tener un mapa más simple: de azul a blanco, o incluso de blanco a azul. Sin embargo, para generar nubes, queremos colocar estratégicamente el color blanco en las "puntas" de nuestro mapa.

Para Subdividir(), el algoritmo es:

Subdividir( matriz, x_i, y_i, x_f, y_f )Si x_f-x_i < 2  Y  y_f-y_i < 2, entonces
Terminar
// Calcular el punto medio
x ← (x_i+x_f) / 2
y ← (y_i+y_f) / 2// Dibujar los puntos medios
Si matriz[x,y_i] < 0, entonces
Generar_Parámetro( matriz, x_i,y_i, x,y_i, x_f,y_i )
PonPíxel( x,y_i, Mapa( matriz[x,y_i] ) )
Si matriz[x_f,y] < 0, entonces
Generar_Parámetro( matriz, x_f,y_i, x_f,y, x_f,y_f )
PonPíxel( x_f,y, Mapa( matriz[x_f,y] ) )
Si matriz[x,y_f] < 0, entonces
Generar_Parámetro( matriz, x_i,y_f, x,y_f, x_f,y_f )
PonPíxel( x,y_f, Mapa( matriz[x,y_f] ) )
Si matriz[x_i,y] < 0, entonces
Generar_Parámetro( matriz, x_i,y_i, x_i,y, x_i,y_f )
PonPíxel( x_i,y, Mapa( matriz[x_i,y] ) )
// Dibujar el punto central = la media de 4 colores
matriz[x,y] ← ( matriz[x_i,y_i] + matriz[x_f,y_i] +
                matriz[x_i,y_f] + matriz[x_f,y_f] ) / 4
PonPíxel( x,y, Mapa( matriz[x,y] ) )// Recursividad
Subdividir( matriz, x_i,y_i, x,y )   // Cuadrante superior izquierdo
Subdividir( matriz, x,y_i, x_f,y )   // Cuadrante superior derecho
Subdividir( matriz, x,y, x_f,y_f )   // Cuadrante inferior derecho
Subdividir( matriz, x_i,y, x,y_f )   // Cuadrante inferior izquierdo
Terminar

Los parámetros x_i, y_i, x_f, y_f contienen los valores de las coordenadas de la esquina superior izquierda (x_i, y_i), y de la esquina inferior derecha (x_f, y_f).

Para Generar_Parámetro(), el algoritmo es:

Generar_Parámetro( parámetros, x_a,y_a, x,y, x_b,y_b )t ← |x_a-x_b| + |y_a-y_b|
t ← Generar_Número(2*t) - t +
     ( parámetros[x_a,y_a] + parámetros[x_b, y_b] + 1 ) / 2
Si t < 0, entonces
t ← 0
Si no, comprueba Si t > 255, entonces
t ← 255
parámetros[x,y] ← t
Terminar

Algunos valores en la matriz parámetros son guardados. Huelga decir que tales cambios deben existir al terminar la función Generar_Parámetro(). En otras palabras, parámetros es un dato entrante y saliente.

Observaciones

Este algoritmo se basa en obtener colores a través de una fórmula paramétrica. El parámetro de dicha fórmula o mapa se obtiene al principio a través de una secuencia de números aleatorios. En nuestro algoritmo, nos interesa manipular cada uno de estos parámetros, en lugar de los colores en sí. Esto es análogo a usar una paleta. En nuestro caso, en vez de guardar los colores generados para luego manipular su índice, calculamos los colores a través de un parámetro. Debemos guardar los parámetros usados mediante la recursividad, por lo que necesitamos una tabla homóloga a la imagen y con las mismas dimensiones. Esto es la tabla parámetros en nuestro algoritmo. La figura 5 muestra esta transformación de nuestro parámetro a un color en nuestro mapa:

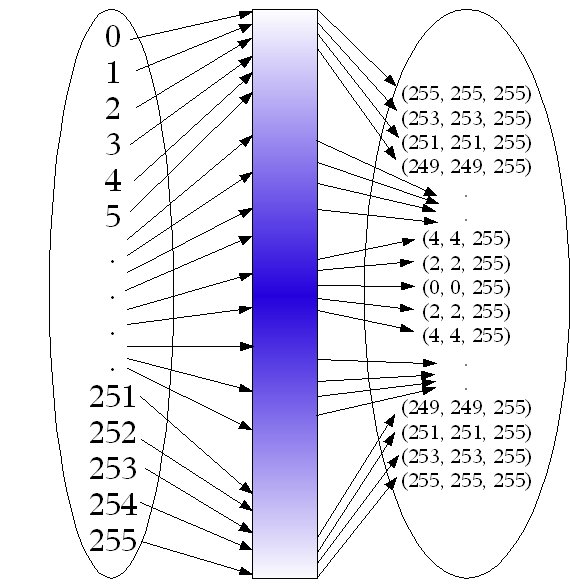
Algunos lectores habrán observado que algunas de las imágenes generadas con este algoritmo tienen una tendencia de formar un rectángulo. Es decir, algunos colores se agrupan de una manera peculiar, creando grupos o brumos con una forma rectangular. Esto se produce debido al método recursivo de nuestro algoritmo, que se basa en calcular los colores de los píxeles de forma rectangular. También es culpable el método de perturbación, ya que la variedad es menor, cuanto menor sea la distancia entre los píxeles. Esto implica que los colores nuevos para píxeles cercanos entre sí no varían mucho de los colores de sus vecinos.

Explicación Detallada

Como se ha explicado anteriormente, este algoritmo se basa en un método recursivo y un método de perturbación para obtener un parámetro que luego es usado para calcular un color en nuestro mapa de colores; o sea, para que un color nuevo pertenezca a nuestra gama de colores. Existen otros métodos para generar este tipo de imágenes. El método más popular y usado es el método de Perlin. Este método se basa en crear un mapa semi-infinito de valores pseudo-aleatorios, que sirven para formar varias frecuencias distintas. Tales frecuencias son sumadas entre sí para crear una función continua. Esta función continua tiene como figura estar formado por grandes perturbaciones en algunos puntos aislados, pero muchas perturbaciones pequeñas a lo largo de toda la función. Con esta función, se puede aplicar varios mapas de colores para generar imágenes muy realistas y naturales; desde nubes en un cielo azul (mejores que con el método que hemos usado), pasando por una textura de madera, granito, hasta texturas de tejidos de lana y algodón.

El método de Perlin se usa para generar texturas, pero también se puede aplicar a animación, para simular movimientos con apariencia aleatoria, pero no caótica. Algunos ejemplos de tal uso puede ser el movimiento de las copas de los árboles en una suave brisa o en un vendaval, o incluso el agiteo de alas de una mariposa o pájaro, hasta incluso la simulación de la caída de copos de nieve en una escena navideña.

Tanto las imágenes generadas por nuestro algoritmo, como las del método de Perlin, se denominan texturas de procedimiento. Estas texturas de procedimiento son un gran alivio para muchos problemas frecuentes al aplicar imágenes rectangulares a objetos en tres dimensiones. Esto es porque las imágenes precreadas deben ser deformadas para ajustarse a las dimensiones del objeto al igual que una distorsión mayor por motivos de perspectiva. Con texturas de procedimiento, cada color puede ser calculada sin depender de las dimensiones del objeto. Como añado, estas texturas se basan en coordenadas de cualquier dimensión: 1D, 2D, 3D, 4D, etc. y por tanto, no existe una transformación de coordenadas de píxeles a coordenadas del objeto, y de vuelta a píxeles. La propia textura se puede usar directamente en cualquier sistema de coordenadas, sin necesidad de un cambio, o al menos no sería impactante.

Huelga decir que, tanto para nuestro método, como el de Perlin, las ímagenes producidas son algo nítidas o marcadas para el cambio de colores. Por lo tanto, nos conviene aplicar un método de suavizado, para mezclar los colores de la imagen. Esto implica que un conjunto de píxeles de colores idénticos o muy parecidos resultará en el mismo conjunto pero de colores iguales, pero seguramente de menor intensidad. Con esto, podemos eliminar esos colores aislados y poblar más área de la imagen con otros colores mayoritarios. El método de suavizado también se llama antialiasing, según los factores que proporcionemos al método.

Trataremos todos estos temas más adelante en el curso, pero aún nos faltan muchos temas y conceptos por tratar.

Ejercicios

Enlace al paquete de este capítulo.

Escriba un programa que implemente el algoritmo descrito en este capítulo para generar nubes. Use una resolución de 400 x 400.

Escriba un programa usando el mapa de colores descrito en cada apartado más abajo, con una resolución de 400 x 400.

Plasma:

Color Mapa( x )Si 0 ≤ x ≤ 85
color.rojo  ← 0
color.verde ← 3*x
color.azul  ← 3*(86-x)
Si 86 ≤ x ≤ 170
color.rojo  ← 3*(86-x)
color.verde ← 3*(171-x)
color.azul  ← 0
Si 171 ≤ x ≤ 255
color.rojo  ← 3*(255-x)
color.verde ← 0
color.azul  ← 3*(x-172)
Terminar( color )

Fuego-Hielo:

Color Mapa( x )color.rojo  ← 255*(1+sen(2*π/256*x))/2
color.verde ← 255*(1+cos(2*π/256*x))/2
color.azul  ← x
Terminar( color )

Topográfico:

Color Mapa( x )
  1. Si 0 ≤ x ≤ 31
    2. color.rojo  ← 64
    3. color.verde ← 127
    4. color.azul  ← 192
  5. Si 32 ≤ x ≤ 62
    6. color.rojo  ← 255
    7. color.verde ← 127
    8. color.azul  ← 0
  9. Si 63 ≤ x ≤ 255
    10. x ← 318-x  // De 255 á 63
    11. color.rojo  ← 255-x/3
    12. color.verde ← 255-x/2
    13. color.azul  ← x
  14. Terminar( color )

Aunque en el algoritmo descrito en este capítulo haga uso de parámetros entre 0 y 255 (ambos incluidos), podemos usar parámetros entre 0,00 y 1,00 (ambos incluidos) como se explicó en la sección, Mapa de Colores. Ahora podemos explicar una forma sencilla de calcular todos los colores entre dos colores conocidos. Se trata del método de interpolación lineal.
En esta fórmula, queremos seguir una progresión lineal entre (x_i, y_i) hasta (x_f, y_f). Nos interesa averiguar el valor y, según un valor x; o sea, nos interesa averiguar (x,y). Por lo tanto, tenemos cuatro valores constantes: x_i, y_i, x_f, y_f; una variable dada: x; y un valor a calcular: y. He aquí la fórmula:
```
Real Interpolación( y_i, y_f, x, x_i, x_f )y ← y_i*(x-x_f)/(x_i-x_f) + y_f*(x-x_i)/(x_f-x_i)
Terminar( y )
```
donde, x_i ≤ x ≤ x_f
Observando esta fórmula, podemos ver que,
Si x = x_i, entonces y = y_i*(x_i-x_f)/(x_i-x_f) + y_f*0 = y_i * 1 = y_i,
Si x = x_f, entonces y = y_i*0 + y_f*(x_f-x_i)/(x_f-x_i) = y_f * 1 = y_f

De esta forma, nos "desplazamos" desde (x_i, y_i) hasta (x_f, y_f), encontrando otros valores que siguen una línea recta.

Por ejemplo, tenemos (2, 5) y (4, 10). Queremos averiguar los valores para la pareja (3, y). Aplicando la fórmula, tenemos que,
```
        (3 - 2)          (3 - 4)
y = 5 * -------  +  10 * ------- = 5/2 + 10/2 = 7,5
        (4 - 2)          (2 - 4)
```
El valor que buscamos es y = 7,50, por lo que tenemos que (3, 7,50).

Tomando el mapa descrito en el ejemplo de la sección, Mapa de Colores, veamos la forma de convertirlo usando interpolación lineal.
```
Color Mapa( i )
1. Si  i ≤ 0,10
   // De Blanco a Azul
   2. color.rojo  ← 255*(0,10-i)/0,10
   3. color.verde ← 255*(0,10-i)/0,10
   4. color.azul  ← 255
5. Si  0,10 < i ≤ 0,50
   // De Azul a Rojo
   6. color.rojo  ← 255*(i-0,10)/0,40
   7. color.verde ← 0
   8. color.azul  ← 255*(i-0,50)/0,40
9. Si  0,50 < i
   // De Rojo a Amarillo
   10. color.rojo  ← 255*(1,00-i)/0,50
   11. color.verde ← 255*(i-1,00)/0,50
   12. color.azul  ← 255*(i-0,50)/0,40
13. Terminar( color )
  
```
Ejercicio 3

Cree algunos mapas basados en esta técnica de interpolación.
Como se hizo en los ejercicios del capítulo 3d - Fractales, es aconsejable crear varias funciones con cada mapa que se desee usar. Luego, al invocar el proceso, pasamos un puntero a la función con el mapa de colores que nos interesa.

Cree más mapas y siga el proceso descrito anteriormente, usando punteros a funciones, para aplicar cualquier mapa de colores a nuestras nubes para formar otras imágenes. Se recomienda mapas de colores que sigan una fluidez de un color a otro con suavidad.
Por ahora, hemos estado creando mapas de colores directamente con el parámetro calculado. Otra fórmula que podemos implementar es en el trato del parámetro. En lugar de escoger un color de nuestro mapa usando el parámetro, aplicaremos una ecuación al parámetro antes de escoger nuestro color.
1. Aplique la función del seno al parámetro. Si se usa el parámetro de 0,00 á 1,00, entonces se puede seguir la siguiente fórmula:
```
parámetro ← (1 + sen( 2π*matriz[x,y] )) / 2
PonPíxel( x,y, Mapa( parámetro ) )
```
  Ejercicio 5a
2. Aplique la función del exponencial al parámetro. De nuevo, si el parámetro se encuentra en el intervalo: [0,00, 1,00], entonces use la siguiente fórmula:
```
parámetro ← (exp(matriz[x,y]) - 1) / (e-1)
PonPíxel( x,y, Mapa( parámetro ) )
```
  donde, e = 2,7182818285 y la función exponencial: exp(x) = e^x
  
  Ejercicio 5b
  
  Observación: Aplicando una función exponencial es una técnica para suavizar una imagen. Compare la imagen de nubes producida con el método descrito en este capítulo y la imagen generada aplicando la función exponencial. En general, se notará una imagen más suave y algo borrosa generada con la función exponencial.
3. Aplique la función del seno hiperbólico al parámetro. Si el parámetro se encuentra en el intervalo: [0,00, 1,00], entonces use la siguiente fórmula:
```
parámetro ← senh(matriz[x,y]) / senh(1)
PonPíxel( x,y, Mapa( parámetro ) )
```
  Ejercicio 5c
4. Aplique la función del coseno hiperbólico al parámetro. Si el parámetro se encuentra en el intervalo: [0,00, 1,00], entonces use la siguiente fórmula:
```
parámetro ← (cosh(matriz[x,y])-1) / (cosh(1)-1)
PonPíxel( x,y, Mapa( parámetro ) )
```
  Ejercicio 5d