Resolución de sudokus (15)
Bugs
Por desgracia ni nuestros algoritmos ni nuestro código está a salvo de errores. Lamentablemente, en algunos de los procedimientos que hemos visto he cometido algunos bastante serios.
Así que dedicaremos este artículo a solucionar algunos de los errores que he detectado hasta ahora.
Durante los últimos meses he puesto a prueba la última versión del programa con varios sudokus que he ido recopilando entre los más difíciles que he jugado. El objetivo era seleccionar aquellos que ilustren algunas de las técnicas de resolución que nos quedan por implementar, pero en el proceso han salido a la luz algunos errores, que o bien impedían detectar ciertos patrones, o los detectaban donde no existían.
Grupos de casillas
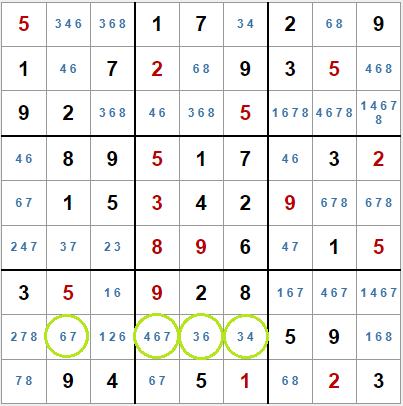
El primer error que vamos a corregir afecta al algoritmo para buscar grupos de casillas que vimos en sudoku 6, porque el algoritmo propuesto no encuentra todos los grupos de casillas posibles.
Por ejemplo, en el sudoku de la derecha, en la octava fila, tenemos siete casillas con candidatos en las que hay un grupo de cuatro casillas que el algoritmo que usamos no es capaz de detectar. Nuestro algoritmo debería haber encontrado el grupo formado por las casillas H2, H4, H5 y H6, que contiene los candidatos 3, 4, 6 y 7, pero el procedimiento que creamos para buscar grupos en el grafo no prueba con todos los posibles caminos y por eso, no localiza este grupo.
Para resolver esto tenemos dos posibilidades. O bien corregimos el procedimiento BuscarGrupo de la clase Grafo, o diseñamos un algoritmo mejor para detectar grupos ocultos.
Además, nuestro programa solo busca grupos de dos, tres o cuatro casillas, pero el caso más desfavorable a la hora de buscar grupos ocultos sería en una fila, columna o caja sin ninguna casilla resuelta. En ese caso, el grupo más grande que tendremos que buscar sería de siete casillas, para encontrar un grupo oculto de dos.
Lo que haremos será buscar otro algoritmo que solucione el problema a la hora de localizar estos grupos.
Para cada fila, columna y caja aplicaremos el siguiente procedimiento:
Creamos una lista para cada casilla con los candidatos que contiene:
1) 2 7 8 2) 6 7 3) 1 2 6 4) 4 6 7 5) 3 6 6) 3 4 7) 5 8) 9 9) 1 6 8
En la práctica, cuando resolvemos sudokus, para hacer las búsquedas de grupos descartaremos las casillas con valores finales, la 7 y 8. Podríamos argumentar que esas dos casillas contienen un par desnudo con los candidatos 5 y 9, pero cualquier información que extraigamos de ahí ya la habremos obtenido previamente al asignar los valores finales.
Si buscamos grupos de dos solo nos interesan las casillas con dos candidatos, la 2, 5 y 6. El objetivo es localizar dos con los mismos candidatos, que en este ejemplo no existen.
Para los grupos de tres nos interesan las casillas con dos o tres candidatos. El objetivo es encontrar grupos de tres casillas con un total de tres candidatos. Es decir, probar todas las combinaciones de tres casillas y contar los candidatos que contienen. En este caso tampoco existen grupos de tres.
Para grupos de cuatro nos quedamos con las casillas con 2, 3 o 4 candidatos, y buscamos todas las combinaciones de cuatro elementos. De este modo llegaríamos a que las casillas 2, 4, 5 y 6 contienen los candidatos 3, 4, 6, 7.
Podemos obviar estas optimizaciones y para cada caso crear todas los posibles combinaciones de dos, tres, cuatro, o más casillas, independientemente del número de candidatos o de si contienen un valor final, y contar cuántos candidatos contiene cada combinación. Si el número coincide, es decir, si una combinación de n casillas contiene n candidatos, tendremos un grupo desnudo, si además esto nos permite eliminar candidatos en alguna de las casillas del resto, habremos aportado información para solucionar el sudoku.
Buscar grupos ocultos
El procedimiento es aplicable para buscar directamente grupos ocultos en lugar de grupos desnudos.
Tan solo tenemos que partir de una tabla de candidatos con una lista de las casillas en las que aparece cada uno, y aplicar el mismo procedimiento.
Para el mismo ejemplo crearíamos una lista para cada candidato con las casillas en que aparece:
1) 3 9 2) 1 3 3) 5 6 4) 4 6 5) 7 6) 2 3 4 5 9 7) 1 2 4 8) 1 9 9) 8
Para buscar grupos ocultos de dos casillas deberemos encontrar dos candidatos que aparezcan únicamente en las mismas dos casillas, es decir, dos candidatos con listas iguales. Para ello podemos eliminar todos los candidatos que aparezcan en solo una casilla (evidentemente), y los que aparezcan en más de dos. En este caso, el 1, 2, 3, 4 y 8. Pero no hay dos candidatos que cumplan esa condición.
Para buscar grupos ocultos de tres casillas eliminamos los candidatos que parezcan en una única casilla y los que aparezcan en más de tres. En este caso, todos menos el 5, 6 y 9. A continuación creamos todos los grupos de tres candidatos y verificamos si contienen o no más de tres casillas. Por ejemplo, los candidatos 1, 2 y 3 aparecen en las casillas 1, 3, 5, 6 y 9. Si seguimos este procedimiento, encontraremos que los candidatos 1, 2 y 8 aparecen en las casillas 1, 3 y 9.
Para el resto de grupos ocultos seguiríamos el mismo procedimiento.
Pero aunque buscar directamente los grupos ocultos sea posible, y técnicamente no requiere usar procedimientos más complejos, esta no es la forma intuitiva de resolver sudokus en la práctica. No resulta fácil ni práctico, ya que no se basa en las marcas de lápiz.
Combinaciones
Lo primero que necesitamos es un procedimiento para encontrar todas las combinaciones de n elementos de un conjunto dado.
Afortunadamente ya tenemos una clase para encontrar esas combinaciones. Tenemos un artículo dedicado a ese tema en algoritmo de combinaciones, que nos permite ir obteniendo las sucesivas combinaciones de un conjunto.
Tomaremos ese algoritmo y aunque lo podríamos optimizar para nuestro caso, de modo que se puedan descartar elementos del conjunto que no nos interese incluir, como los valores finales o las casillas con más candidatos que el tamaño de la combinación que buscamos, y esto seguramente mejoraría el rendimiento del programa, de momento no lo haremos.
Código
Para empezar, eliminamos la clase Grafo de nuestro proyecto.
Partiendo de la plantilla para generar combinaciones vamos a diseñar una nueva clase Grupo que se encargará de obtener las combinaciones de casillas, y añadiremos algunos métodos para facilitar la detección de grupos.
// Sudokus con Clase
// Resolución de sudokus con técnicas reales
// (C) 2023 Salvador Pozo
// Con Clase https://conclase.net
//
// Declaración de la clase Grupo
//
// Se usa para detectar parejas, trios, cuartetos... ocultos
#ifndef SUDOKU_GRUPO
#define SUDOKU_GRUPO
#include "casilla.h"
#include "marcaslapiz.h"
#include "combinaciones.h"
class Grupo {
private:
int valor[9];
Combinacion<Casilla *> comb;
public:
Grupo(Casilla *c[9]) : comb(c, 9) {}
bool PrimeraCombinacion(int nElementos) { return comb.PrimeraCombinacion(nElementos); }
bool SiguienteCombinacion() { return comb.SiguienteCombinacion(); }
Casilla *Comb(int index) const { return comb.Comb()[index]; }
bool Contiene(Casilla *cas, int nElementos);
char *Casillas(int);
char *Valores(MarcasLapiz marcas, int);
};
#endif // SUDOKU_GRUPO
En la clase Tablero eliminamos el código referente a Grafo y lo sustituimos por el nuevo usando Grupo.
Tenemos tres métodos privados:
bool ProcesaGrupoFila(int grupo, int nElementos);
bool ProcesaGrupoColumna(int grupo, int nElementos);
bool ProcesaGrupoCaja(int grupo, int nElementos);
Para buscar grupos en filas, columnas o cajas. En cada caso indicamos el número de fila, columna o caja y el número de elementos del grupo a buscar.
Un método público:
bool ProcesaGrupo(int nElementos);
Que llamará a los métodos privados para cada fila, columna y caja buscando grupos de nElementos.
bool Tablero::ProcesaGrupo(int nElementos) {
bool retval = false;
for(int f=0; f<9; f++) {
retval |= ProcesaGrupoFila(f, nElementos);
}
for(int c=0; c<9; c++) {
retval |= ProcesaGrupoColumna(c, nElementos);
}
for(int k=0; k<9; k++) {
retval |= ProcesaGrupoCaja(k, nElementos);
}
return retval;
}
Los tres métodos privados son semejantes, veamos el correspondiente a las filas:
bool Tablero::ProcesaGrupoFila(int f, int nElementos) {
Grupo grupo(fila[f].GetCasillas());
MarcasLapiz marcas;
bool retval = false;
if(grupo.PrimeraCombinacion(nElementos)) {
do {
marcas = MarcasLapiz(0);
for(int i = 0; i<nElementos; i++) {
if(grupo.Comb(i)->Valor()) marcas = marcas + 0x1ff; // Ignorar grupos con casillas finales
else marcas = marcas + grupo.Comb(i)->Lapiz();
}
if(marcas.CuentaMarcas() == nElementos) {
for(int i = 0; i<9; i++) {
if(!grupo.Contiene(fila[f].Cas(i), nElementos)) {
retval |= (fila[f].Cas(i)->Lapiz() ^ marcas).CuentaMarcas();
}
}
if(retval) { // Tenemos un grupo que aporta información
for(int c=0; c<9; c++) {
for(int v=1; v<=9; v++) {
if(marcas.ContieneMarca(v) && !grupo.Contiene(fila[f].Cas(c), nElementos) && fila[f].Cas(c)->Lapiz().ContieneMarca(v)) {
fila[f].Cas(c)->Lapiz().EliminaMarca(v);
}
}
}
}
}
} while(grupo.SiguienteCombinacion());
}
return retval;
}
Iremos generando combinaciones sucesivamente. Para cada una calcularemos las marcas de lápiz que contiene. Para evitar tener en cuenta combinaciones que contengan casillas con valor final, añadiremos las nueve marcas para esas casillas.
Si el número de marcas de la combinación coincide con el número de elementos, verificamos su alguna del resto de casillas contiene alguno de los valores de la combinación. Esto evitará procesar grupos que no permitan eliminar candidatos.
Finalmente eliminamos los candidatos del grupo del resto de casillas de la fila.
El constructor recibe como parámetro un array de punteros a Casilla que puede ser una fila, columna o caja en las que buscaremos grupos, y las usa para crear una instancia privada de la plantilla Combinacion de objetos Casilla.
Los métodos PrimeraCombinacion y SiguienteCombinacion son simplemente un interfaz para acceder a los métodos homónimos de la plantilla Combinacion.
El método Comb nos permite recuperar la casilla indicada en el parámetro de la última combinación generada.
El método Contiene devolverá true si la combinación actual contiene la casilla indicada en el parámetro.
Los otros dos métodos Casillas y Valores se usan para mostrar información en pantalla y generar el fichero log con el procedimiento de resolución.
Finalmente, en main podemos invocar el método ProcesaGrupo con valores de parámetro entre 2 y 7.
Sashimi X-Wing
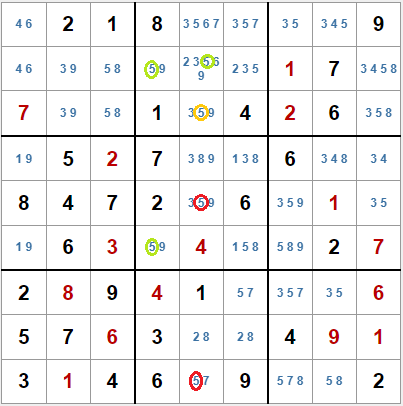
Intentando resolver el sudoku de la derecha, el programa llega a una situación de error, con valores repetidos y casillas sin candidatos.
El error se produce al detectar patrones Sashimi X-Wing, y como resultado procesa determinadas configuraciones como si lo fueran y elimina candidatos que no debería eliminar.
Como vimos en Sudoku 12, un patrón Sashimi X-Wing es similar a un patrón X-Wing con alas, en el que en la caja con las alas la casilla correspondiente al patrón X-Wing no contiene el candidato.
Como vemos en el sudoku del ejemplo, ese no es el patrón que se ha detectado. Para empezar, las dos columnas están en la misma columna de cajas. Además, en la segunda columna aparecen candidatos en la fila de cajas que no pertenece al patrón, y para terminar, se elimina el candidato del ala, en lugar de los que se pueden eliminar según el método. (No sé cómo pude programar tan mal este algoritmo).
Existen cuatro posibles configuraciones para este patrón:
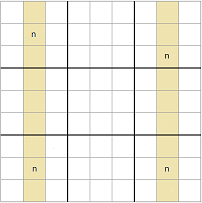
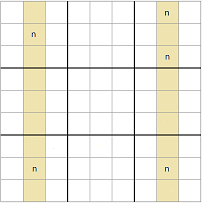
- Por columnas, con un ala
- Por columnas, con dos alas.
- Por filas, con un ala.
- Por filas, con dos alas.
Nos centraremos en los patrones por columnas, ya que los otros dos solo cambian filas por columnas.
Un patrón Sashimi X-Wing por columnas correcto debe cumplir las siguientes condiciones:
- Una de las columnas solo puede tener dos candidatos, en cajas diferentes.
- La otra columna debe tener un candidato en la misma fila que una de las casillas de la primera columna.
- En la caja correspondiente a la casilla que debería completar el patrón X-Wing puede haber una o dos alas, en la misma columna que la casilla anterior.
La variante con un ala es lo que denominamos un patrón rascacielos, que hemos tratado a parte, y por lo que parece, sin cometer errores.
Por lo tanto, nos centraremos en los casos b y d.
En cada uno de estos casos hay dos variantes del patrón: b, en el que las alas están en la caja superior y b', en el que las alas están en la caja inferior.
El algoritmo es semejante para filas y columnas, nos centraremos en las filas.
El procedimiento empieza igual, buscando para cada candidato una fila en la que aparezca solo en dos casillas, pero que no estén en la misma caja.
A continuación calcularemos las columnas en las que pueden estar las dos alas del patrón.
Buscaremos en las filas que no estén en la misma fila de cajas alguna en la que el candidato aparezca tres veces en las casillas en que debe aparecer, ya sea el patrón b o b'.
Si se detecta el patrón, lo procesaremos para averiguar si se puede eliminar algún candidato, y en ese caso, eliminarlo.
Código
Nuestro nuevo método para buscar patrones Sashimi X-Wing es:
bool Tablero::BuscaSashimiFilas() {
Pareja par;
int c1, c2;
int c1a, c1b, c2a, c2b;
for(int v=1; v<=9; v++) {
for(int f1=0; f1<8; f1++) {
par = fila[f1].DobleCandidato(v);
if(par.Cas(0) && !par.MismaCaja() ) {
c1 = par.Cas(0)->Columna();
c2 = par.Cas(1)->Columna();
// Calcular las columnas donde pueden estar las alas:
switch(c1%3) {
case 0: c1a=3*(c1/3)+1; c1b=3*(c1/3)+2; break;
case 1: c1a=3*(c1/3)+0; c1b=3*(c1/3)+2; break;
case 2: c1a=3*(c1/3)+0; c1b=3*(c1/3)+1; break;
}
switch(c2%3) {
case 0: c2a=3*(c2/3)+1; c2b=3*(c2/3)+2; break;
case 1: c2a=3*(c2/3)+0; c2b=3*(c2/3)+2; break;
case 2: c2a=3*(c2/3)+0; c2b=3*(c2/3)+1; break;
}
for(int f2=0; f2<9; f2++) {
// Las dos filas deben estar en cajas diferentes, y la segunda debe tener el candidato tres veces
if(casilla[f1][c1].Caja() != casilla[f2][c1].Caja() && fila[f2].CuentaCandidato(v) == 3) {
if(casilla[f2][c1].Lapiz().ContieneMarca(v) && !casilla[f2][c2].Lapiz().ContieneMarca(v) &&
casilla[f2][c2a].Lapiz().ContieneMarca(v) && casilla[f2][c2b].Lapiz().ContieneMarca(v)){
if(ProcesarSashimiColumna(f1, f2, c1, c2, v, c2, c2a, c2b)) return true;
}
if(casilla[f2][c2].Lapiz().ContieneMarca(v) && !casilla[f2][c1].Lapiz().ContieneMarca(v) &&
casilla[f2][c1a].Lapiz().ContieneMarca(v) && casilla[f2][c1b].Lapiz().ContieneMarca(v)) {
if(ProcesarSashimiColumna(f1, f2, c1, c2, v, c1, c1a, c1b)) return true;
}
}
}
}
}
}
return false;
}
Y para procesar el patrón detectado:
bool Tablero::ProcesarSashimiFila(int f1, int f2, int c1, int c2, int v, int c, int ca, int cb) {
int retval = false;
int k = casilla[f2][c].Caja();
char cad[100];
for(int p=0; p<9; p++) {
if(caja[k].Cas(p)->Columna() == c) retval |= caja[k].Cas(p)->Lapiz().ContieneMarca(v);
}
if(retval) {
for(int p=0; p<9; p++) {
if(caja[k].Cas(p)->Columna() == c)
caja[k].Cas(p)->Lapiz().EliminaMarca(v));
}
}
return retval;
}
Con esto tenemos una versión corregida que aplica correctamente los métodos de resolución que hemos visto hasta ahora, salvo que surjan errores que aún no se han manifestado.
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku20 | sudoku20.zip | 2023-08-16 | 36472 bytes | 544 |