Resolución de sudokus (6)
Parejas, trios y cuartetos ocultos.
Parejas, trios y cuartetos ocultos
Si hay que llegar a este punto para resolver un sudoku ya podemos considerarlo como difícil. El criterio es que hasta ahora hemos trabajado con bloques: filas, columnas y cajas, pero a partir de ahora tenemos que trabajar con casillas individuales de todo el tablero. La diferencia puede parecer sutil, pero se necesita más concentración y mas tiempo para localizar las relaciones entre casillas con los métodos que veremos a partir de ahora. Y eso irá en aumento a medida que tengamos que recurrir a métodos más complejos.
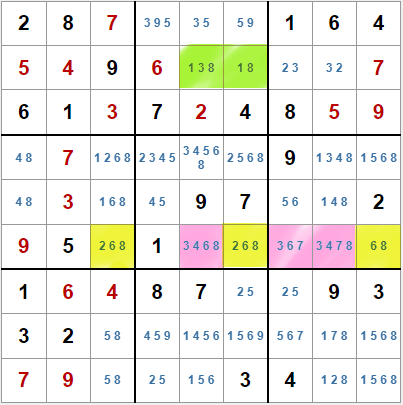
Una pareja o trio oculto se localizará a través de otras parejas o trios previamente conocidos. Por ejemplo, en el sudoku de la imagen de marcas de lápiz, para localizar la pareja en verde usaríamos la otra pareja de la línea (2,3), que elimina el valor 3 de la quinta casilla.
En general tendremos que partir siempre de una pareja, trio o incluso cuartetos o quintetos no ocultos para poder detectar algún grupo oculto. De modo que nuestra primera tarea es localizar esos grupos de dos, tres o cuatro casillas.
A medida que vayamos eliminado candidatos de casillas pueden aparecer nuevas parejas o trios desnudos de forma automática, de modo que seguiremos buscándolos y procesándolos.
Clase para marcas de lápiz
Para los algoritmos que usaremos a partir de ahora no resulta práctico trabajar un arrays para almacenar y manipular marcas de lápiz.
Necesitaremos hacer algo de aritmética con esas marcas de lápiz. Concretamente, necesitaremos saber qué marcas tienen en común dos casillas, y cuántas marcas tienen en conjunto varias casillas.
Lo ideal sería poder sumar marcas para saber cuántas y cuales tienen en conjunto dos o más casillas, y restarlas para saber cuántas y cuales no tienen en común y usar otro operador para saber cuántas y cuáles tienen en común.
Así que modificaremos el programa para añadir una nueva clase MarcasLapiz, y poder incorporar esta aritmética, de modo que nuestros algoritmos se simplifiquen notablemente.
class MarcasLapiz {
private:
unsigned int lapiz;
public:
MarcasLapiz(unsigned int l=0) : lapiz(l) {}
MarcasLapiz(const MarcasLapiz &m) { lapiz = m.lapiz; }
bool AsignaMarca(int v);
bool EliminaMarca(int v);
int CuentaMarcas();
bool ContieneMarca(int v);
MarcasLapiz &operator=(const MarcasLapiz &m1) { lapiz = m1.lapiz; return *this; };
MarcasLapiz operator+(const MarcasLapiz &m1);
MarcasLapiz operator^(const MarcasLapiz &m1);
MarcasLapiz operator-(const MarcasLapiz &m1);
bool operator==(const MarcasLapiz &m1) { return this->lapiz == m1.lapiz; }
bool Quitar(const MarcasLapiz &m1);
};
La implementación es oscuramente simple:
bool MarcasLapiz::AsignaMarca(int v) {
if(lapiz & 1<<(v-1)) return false;
lapiz |= 1<<(v-1);
return true;
}
bool MarcasLapiz::EliminaMarca(int v) {
if((lapiz & 1<<(v-1)) == 0) return false;
lapiz &= ~(1<<(v-1));
return true;
}
int MarcasLapiz::CuentaMarcas() {
int c=0;
for(int v=1; v<=9; v++) if(ContieneMarca(v)) c++;
return c;
}
bool MarcasLapiz::ContieneMarca(int v) {
return (lapiz & 1<<(v-1));
}
MarcasLapiz MarcasLapiz::operator+(const MarcasLapiz &m1) {
MarcasLapiz res(0);
res.lapiz = this->lapiz | m1.lapiz;
return res;
}
MarcasLapiz MarcasLapiz::operator^(const MarcasLapiz &m1) {
MarcasLapiz res(0);
res.lapiz = this->lapiz & m1.lapiz;
return res;
}
MarcasLapiz MarcasLapiz::operator-(const MarcasLapiz &m1) {
MarcasLapiz res(0);
res.lapiz = (this->lapiz | m1.lapiz) & ~(this->lapiz & m1.lapiz);
return res;
}
bool MarcasLapiz::Quitar(const MarcasLapiz &m1) {
if(!(lapiz & m1.lapiz)) return false;
lapiz &= ~m1.lapiz;
return true;
}
Lo que hace esta clase es almacenar las marcas de lápiz en bits, y trabajar con máscaras para individualizar cada uno. Así, por ejemplo, para saber si una marca está activa para un valor v, rotamos un bit a la izquierda v-1 posiciones, y hacemos una operación AND con las marcas almacenadas.
Contar marcas es también sencillo. Hemos optado por contar los bits activos para cada posible valor de 1 a 9, pero podríamos haber rotado las marcas a la derecha nueve veces y contar las veces que el bit 1 se activa.
Para la aritmética hemos sobrecargado los operadores de suma, resta y ^. La suma es una operación OR de bits. El operador ^ calculará la intersección, es decir, las marcas comunes, usando la operación AND de bits. La resta calculará las marcas no comunes, es decir AND entre la suma y el complemento de los comunes.
También sobrecargamos el operador de asignación y el de comparación, y añadiremos una función para eliminar las marcas de lápiz que pasaremos como parámetro.
Localizar grupos de casillas
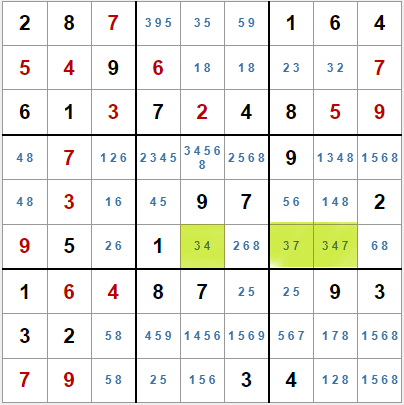
Pero volvamos al tablero actual (marcas de lápiz final). En la sexta fila tenemos seis casillas libres. En teoría podría haber como mucho tres pares desnudos o dos trios desnudos ocultos. Pero para poder detectarlos tendremos que localizar al menos un par o trio desnudo. Veremos más tarde que nuestro algoritmo puede localizar grupos de cualquier tamaño, aunque el tamaño máximo en la práctica sea de siete elementos, que nos permitiría localizar una pareja desnuda oculta.
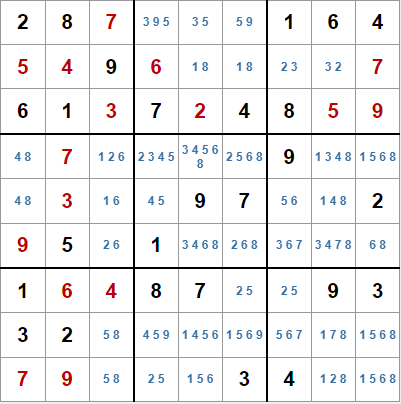
Tenemos las siguientes marcas de lápiz:
- 3): 2, 6
- 5): 3, 4, 6, 8
- 6): 2, 6, 8
- 7): 3, 6, 7
- 8): 3, 4, 7, 8
- 9): 6, 8
Para localizar pares solo nos interesan casillas con dos marcas de lápiz, de otro modo se trataría de un par escondido, y sería imposible de detectar.
Las casillas con dos marcas son la tercera y novena, que no forman un par, ya que no tienen las mismas marcas.
Para localizar los trios tomaremos las casillas con dos o tres marcas de lápiz:
- 3): 2, 6
- 6): 2, 6, 8
- 7): 3, 6, 7
- 9): 6, 8
Necesitamos elegir tres de ellas que tengan tres marcas de lápiz en común. Por lo que podemos descartar las casillas que contengan una marca de lápiz que solo aparezca una vez. En este caso, la séptima casilla que contiene el único 7.
En este ejemplo solo quedan tres casillas, si entre las tres solo tienen marcas de lápiz para tres valores, habremos encontrado un trio desnudo. Si hubiera más casillas tendremos que probar diferentes combinaciones de tres casillas.
Por ejemplo, en la quinta fila tenemos las siguientes casillas con dos o tres marcas de lápiz:
- 1): 4, 8
- 3): 1, 6
- 4): 4, 5
- 7): 5, 6
- 8): 1,4, 8
No hay pares desnudos, ya que no se repiten las mismas marcas de lápiz en dos casillas.
Para buscar trios no podemos eliminar ninguna casilla, así que tomaremos combinaciones de casillas de tres en tres.
- La 1 y la 3 no pueden formar parte de un trio, ya que entre las dos tienen cuatro marcas de lápiz.
- La 1 y la 4 sí pueden, pero no forman un trio ni con la 7, ni con la 8.
- La 3 y la 4 no se pueden combinar.
- La 3 y la 7 sí, pero no se puede combinar con la 8.
- La 4, 7 y 8 tampoco forman un trio.
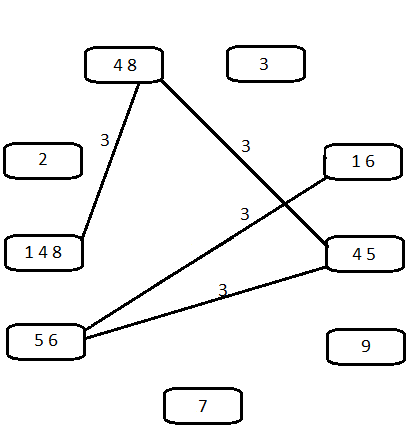
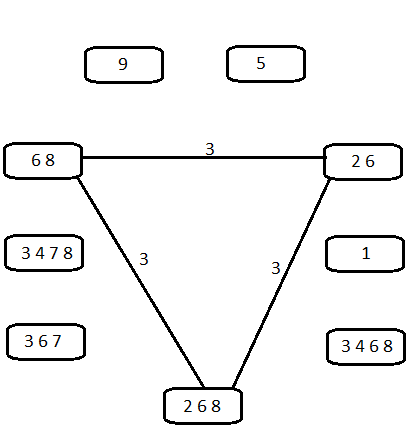
Podemos resolver esto mucho más fácilmente con un método más visual, usando grafos.
Creamos un nodo para cada casilla, y los unimos con aristas. Ignoraremos las casillas con un valor asignado y con más marcas de lápiz que elementos del grupo que buscamos. Tampoco añadiremos aristas entre casillas sin marcas de lápiz en común. El valor de cada arista se calcula sumando el número de marcas comunes y no comunes, si ese valor también es mayor que el número de elementos, no añadiremos esa arista. Una vez añadida una arista, su valor es irrelevante.
Para la quinta fila nos queda el grafo de la izquierda, y para la sexta el de la derecha.
Ahora eliminaremos aristas y nodos con el siguiente criterio: si un nodo tiene dos aristas menos que el tamaño del grupo podemos eliminar ese nodo, eliminando todas sus aristas. Esto es porque para formar un grupo de n casillas, cada una de las casillas tiene que tener elementos comunes con otras n-1. Por lo tanto, si solo se relaciona con n-2 o menos, no es posible que forme parte de un grupo.
Si en el grafo de la quinta fila aplicamos este criterio nos quedamos sin aristas, por lo que no podremos formar grupos de tres casillas.
Finalmente buscaremos recorridos cerrados de n casillas con n valores diferentes.
En la práctica lo que haremos es, para las casillas que contengan alguna arista, formar un grupo con ellas y con todas las relacionadas y verificar si cumplen las condiciones para formar un grupo desnudo: que el número de casillas y el número de marcas de lápiz del conjunto sea el mismo.
En el grafo de la sexta fila nos quedan tres casillas conectadas, y podemos recorrerlas siguiendo las aristas. Esto significa que esas tres casillas forman un trio desnudo. Una vez eliminadas las marcas de lápiz del trio en el resto de casillas, si repetimos el proceso, veremos que se pueden definir dos trios. Es decir, hemos descubierto un trio oculto.
Hay que tener en cuenta que una zona del sudoku puede contener varios grupos desnudos. En nuestro ejemplo, en la segunda línea hay dos pares desnudos, con las marcas de lápiz (1,8) y (2,3). Esto puede ocurrir también con trios, y que aún pueda haber grupos ocultos en la misma zona. Por lo tanto, deberemos tener esto en cuenta en nuestro algoritmo.
Para programar este procedimiento crearemos una nueva clase Grafo encargada de realizar todas las tareas de detección de grupos:
class Grafo {
private:
int grupo;
Casilla **cas;
int nAristas[9];
bool arista[9][9];
bool nodo[9];
bool valor[9];
MarcasLapiz marcas;
int valor[9];
int nod[9];
public:
Grafo(int gr) : grupo(gr) {}
void IniciarMarcas(Casilla **c) { cas = c; }
void AsignarAristas();
void EliminarAristasUnicas();
bool BuscarGrupo();
void EliminarGrupo();
int Nodo(int n);
int Valor(int n);
bool Contiene(int p);
};
Esta clase contiene un puntero a un grupo de casillas (fila, columna o caja), un array de aristas entre nodos correspondientes a las nueve casillas del grupo, y algunas variables auxiliares, como el número de aristas por nodo, y dos arrays con los nodos y aristas. Usaremos un objeto de la clase MarcasLapiz para almacenar las marcas de lápiz del grupo.
Este procedimiento nos permite localizar cualquier grupo desnudo, que a su vez nos permitirá, con algo de suerte, eliminar algunos candidatos para algunas casillas, y desvelar otros grupos ocultos.
Expliquemos algunos métodos:
AsignarAristas se encarga de asignar todas las aristas entre los nodos.
void Grafo::AsignarAristas() {
MarcasLapiz marcas;
// Eliminamos cualquier arista de un nodo consigo mismo
for(int i=0; i<9; i++) {
nAristas[i]=0;
arista[i][i] = false;
}
for(int c1=0; c1<8; c1++) {
for(int c2=c1+1; c2<9; c2++) {
// Inicialmente eliminamos las aristas
arista[c1][c2]= arista[c2][c1] = false;
if(!cas[c1]->Valor() && !cas[c2]->Valor() &&
cas[c1]->Lapiz().CuentaMarcas() <= grupo &&
cas[c2]->Lapiz().CuentaMarcas() <= grupo) {
marcas = cas[c1]->Lapiz() + cas[c2]->Lapiz();
if(marcas.CuentaMarcas() <= grupo) {
nAristas[c1]++;
nAristas[c2]++;
arista[c1][c2]= arista[c2][c1] = true;
}
}
}
}
EliminarAristasUnicas();
}
Se trata de dos bucles anidados que recorren las casillas comparándolas dos a dos. Tenemos dos condicionantes. En el primero descartamos casillas con valor final y con más marcas de lápiz que el tamaño del grupo que estamos buscando. En el segundo seleccionamos la pareja de casillas en la que la suma de marcas de lápiz es menor o igual al tamaño del grupo. En ese caso añadimos las aristas y actualizamos la cuenta.
EliminarAristaasUnicas se encarga de eliminar todas las aristas de aquellos nodos que tengan entre una y el tamaño del grupo menos dos aristas:
void Grafo::EliminarAristasUnicas() {
bool repetir;
do {
repetir = false;
for(int c1=0; c1<9; c1++) {
if(nAristas[c1]>0 && nAristas[c1]<=grupo-2) {
repetir = true;
for(int c2=0; c2<9; c2++) {
if(arista[c1][c2]) {
nAristas[c1]--;
nAristas[c2]--;
arista[c1][c2] = arista[c2][c1] = false;
}
}
}
}
} while(repetir);
}
BuscaGrupo se dedica a buscar un grupo que cumpla las condiciones necesarias, es decir, que esté formado por grupo casillas y que entre todas tengan grupo marcas de lápiz:
bool Grafo::BuscarGrupo() {
int nNodos;
for(int c1=0; c1<9; c1++) {
for(int c=0; c<9; c++) nodo[c] = false;
marcas = MarcasLapiz(0);
nNodos = 0;
if(nAristas[c1] > 0) {
nNodos++;
nodo[c1] = true;
marcas = marcas + cas[c1]->Lapiz();
for(int c2=c1+1; c2<9; c2++) {
if(arista[c1][c2]) {
nNodos++;
nodo[c2] = true;
marcas = marcas + cas[c2]->Lapiz();
}
}
if(nNodos == grupo && marcas.CuentaMarcas() == grupo) {
for(int i=0,n=0; n<9; n++) if(nodo[n]) nod[i++] = n;
for(int i=0,v=1; v<=9; v++) if(marcas.ContieneMarca(v)) valor[i++] = v;
return true;
}
}
}
return false;
}
Si encuentra un grupo válido, actualiza los arrays internos nod con los índices de las casillas que forman el grupo y valor con los valores de las marcas de lápiz.
Para procesar el tablero buscando y procesando los grupos encontrados añadiremos algunos métodos a la clase Tablero:
class Tablero {
private:
...
bool ProcesarGrafoFila(int grupo);
bool ProcesarGrafoColumna(int grupo);
bool ProcesarGrafoCaja(int grupo);
...
public:
bool ProcesarGrafo(int grupo);
...
};
Los procedimientos para procesar los grafos para filas, columnas y cajas son similares:
bool Tablero::ProcesaGrafoFila(int grupo) {
Grafo g(grupo);
bool retval = false;
// Para cada fila:
for(int f=0; f<9; f++) {
g.IniciarMarcas(fila[f].GetCasillas());
g.AsignarAristas();
// Para cada grupo existente
while(g.BuscarGrupo()) {
// Eliminar candidatos en resto de fila:
for(int c=0; c<9; c++) {
if(!g.Contiene(c)) {
for(int i=1; i<=grupo; i++) {
fila[f].Cas(c)->Lapiz().EliminaMarca(g.Valor(i));
}
}
}
g.EliminaGrupo();
}
}
return retval;
}
El procedimiento es sencillo, elimina las marcas de lápiz del grupo en las casillas de la zona salvo en las que forman parte del grupo. En el programa de ejemplo estas funciones son algo más largas para añadir las salidas de texto con las instrucciones.
Para columnas y cajas las funciones son análogas.
Necesitamos añadir el método GetCasillas a las clases Fila, Columna y Caja para obtener punteros a las casillas que forman cada grupo desde la clase Grafo:
class Fila {
private:
...
Casilla **GetCasillas() { return cas; }
...
};
Para buscar todos los grupos en cada fila, columna y caja usaremos el método ProcesarGrafo.
bool Tablero::ProcesarGrafo(int grupo) {
bool retval = false;
retval |= ProcesarGrafoFila(grupo);
retval |= ProcesarGrafoColumna(grupo);
retval |= ProcesarGrafoCaja(grupo);
return retval;
}
Bucle de resolución
Ya solo nos queda añadir las llamadas para procesar el tablero en busca de grupos de diferentes tamaños:
do {
...
if(!repetir && T.ProcesaGrafo(2)) {
repetir =true;
T.VerificarFinales();
}
if(!repetir && T.ProcesaGrafo(3)) {
repetir =true;
T.VerificarFinales();
}
...
} while(repetir);
Se pueden procesar también grupos de 4, 5, 6 y 7 casillas.
En nuestro ejemplo hemos eliminado algunos candidatos de la sexta fila, lo que nos deja el sudoku preparado para aplicar el siguiente método.
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku6 | sudoku6.zip | 2022-06-22 | 21476 bytes | 665 |