Resolución de sudokus (8)
X-Wing y X-Wing con alas.
X Wing
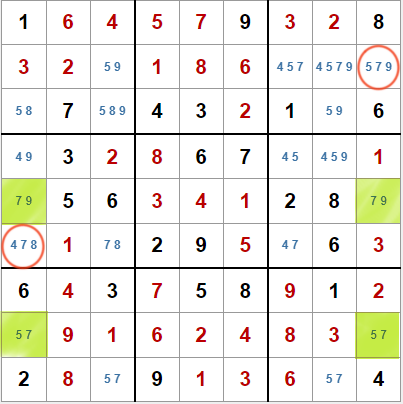
Aún existen situaciones en las que ninguna de las técnicas anteriores nos puede ayudar a resolver el sudoku. Veamos ahora otra técnica que podemos probar.
La técnica X Wing consiste en encontrar un valor de marca de lápiz que aparezca en cuatro casillas en solo dos filas y dos columnas, pero que o bien en las dos filas o bien en las dos columnas, sean las únicas casillas donde aparezcan.
En el sudoku del ejemplo el valor candidato compartido por las cuatro casillas es el 7. Es evidente que ese valor tiene que estar en las casillas E5 y H9, o bien en las casillas H1 y E9, ya que son las únicas casillas de cada fila en que aparecen como candidato. Esto descarta el valor 7 del resto de las casillas de la primera y novena columnas.
Empezaremos por buscar filas con candidatos que solo aparezcan en dos casillas. Si se localiza, buscaremos el mismo candidato en las filas restantes y en solo las mismas columnas, y eliminaremos las marcas de lápiz del valor común de esas cuatro casillas en el resto de las casillas de esas dos columnas.
Repetiremos todo el proceso con las columnas.
Crearemos una nueva clase auxiliar para almacenar parejas de casillas. Esto nos ayudará a simplificar los métodos para detectar situaciones X-Wing:
class Pareja {
private:
Casilla *cas[2];
public:
Pareja() { cas[0] = cas[1] = NULL; }
Casilla *Cas(int c) { return cas[c]; }
void Asigna(int p, Casilla *c) { if(p < 2) cas[p] = c; };
};
También añadiremos un método DobleCandidato a las clases Fila y Columna. Buscará marcas de lápiz que aparezcan solo dos veces en una fila o columna:
Pareja Fila::DobleCandidato(int v) {
int cuenta=0;
Pareja par;
for(int c=0; c<9; c++) {
if(cas[c]->Lapiz().ContieneMarca(v)) par.Asigna(cuenta++, cas[c]);
}
if(cuenta==2) return par;
return Pareja();
}
Por último, añadiremos tres nuevos métodos a la clase Tablero:
class Tablero {
private:
...
bool ProcesaXWingFila(Pareja a, Pareja b, int v);
bool ProcesaXWingColumna(Pareja a, Pareja b, int v);
...
public:
...
bool ProcesaXWing();
};
El método ProcesaXWing procesará las filas y columnas buscando patrones X-Wing
bool Tablero::ProcesaXWing() {
Pareja par1, par2;
for(int v=1; v<=9; v++) { // Para cada valor
// Empezamos con las filas. No buscaremos en la última,
// ya que no podemos comparar con las siguientes
for(int f=0; f<8; f++) {
// Detectar fila con dos casillas con el candidato v
par1 = fila[f].DobleCandidato(v);
// Si par1(0) != NULL, tenemos un candidato a X-Wing, buscaremos en el resto de filas
if(par1.Cas(0) != NULL) {
for(int f2=f+1; f2<9; f2++) {
par2 = fila[f2].DobleCandidato(v);
if(par2.Cas(0) != NULL &&
par1.Cas(0)->Columna() == par2.Cas(0)->Columna() &&
par1.Cas(1)->Columna() == par2.Cas(1)->Columna()) {
if(ProcesaXWingFila(par1, par2, v)) return true;
}
}
}
}
// Y ahora las columnas.
for(int c=0; c<8; c++) {
// Detectar fila con dos casillas con el candidato v
par1 = columna[c].DobleCandidato(v);
// Si par1(0) != NULL, tenemos un candidato a X-Wing, buscaremos en el resto de columnas
if(par1.Cas(0) != NULL) {
for(int c2=c+1; c2<9; c2++) {
par2 = columna[c2].DobleCandidato(v);
if(par2.Cas(0) != NULL &&
par1.Cas(0)->Fila() == par2.Cas(0)->Fila() &&
par1.Cas(1)->Fila() == par2.Cas(1)->Fila()) {
if(ProcesaXWingColumna(par1, par2, v)) return true;
}
}
}
}
}
return false;
}
Y procesaremos cada patrón X-Wing:
bool Tablero::ProcesarXWingFila(Pareja a, Pareja b, int v) {
bool retval=false;
for(int f=0; f<9; f++) {
if(f != a.Cas(0)->Fila() && f != b.Cas(0)->Fila()) {
retval |= casilla[f][a.Cas(0)->Columna()].Lapiz().EliminaMarca(v);
retval |= casilla[f][a.Cas(1)->Columna()].Lapiz().EliminaMarca(v);
}
}
return retval;
}
Para procesar patrones X-Wing en columnas la función es análoga.
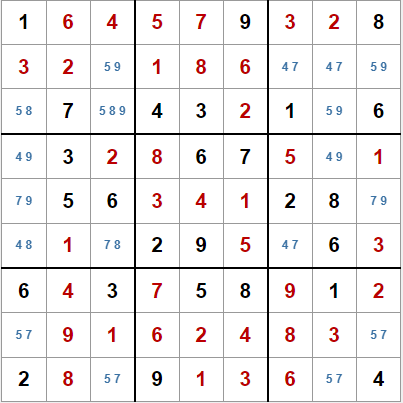
Aún aplicando esta técnica, este sudoku en particular se sigue resistiendo. Hemos eliminado algunos candidatos y revelado el valor de una casilla, pero de nuevo nos encontramos con que ninguna de las técnicas que hemos visto hasta ahora aporta información nueva.
Volveremos a este sudoku tal como está ahora en un capítulo posterior, ya que tiene una característica muy interesante: todas las casillas vacías tienen dos candidatos, excepto una que tiene tres. Cuando se de ésta situación, con la técnica adecuada, podemos resolver el sudoku completo en una operación.
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku8 | sudoku8.zip | 2022-06-22 | 24437 bytes | 615 |
X-Wing con alas
Nota: ya que X-Wing significa "alas en X", parece redundante añadir más alas. En realidad deberíamos traducir esta técnica como X-Wing con aletas o con alerones, ya que lo que se sugiere es que aparecen añadidos en una de las alas.
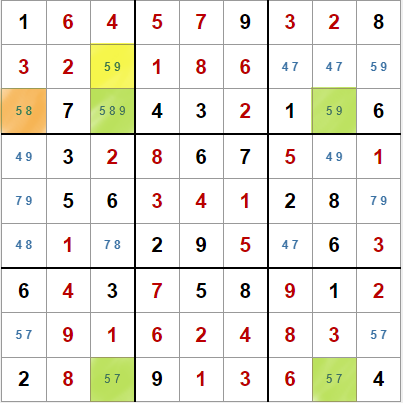
Esta técnica es una variante o generalización del método X-Wing. En la imagen de la izquierda tenemos dos posibles situaciones X-Wing con alas.
Para empezar, partimos de cuatro casillas con el valor 5 común en dos filas y columnas, en verde en la imagen.
Para el primer patrón consideremos las filas tercera y novena. Vemos que en la tercera hay tres casillas con el valor 5, la tercera en naranja, es la que llamaremos 'aleta'.
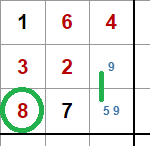
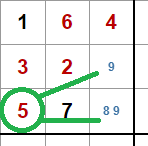
Ahora consideremos dos posibilidades:
- El valor 5 está en la aleta: esto eliminaría como candidato los 5 en el resto de las casillas de la primera caja.
- Ahora consideremos que el 5 no está en la aleta: esto nos deja una situación X-Wing, lo que eliminaría como candidato el 5 del resto de casillas de la tercera columna de la primera caja.
En ningún caso el valor 5 de la casilla en amarillo será un candidato, y por lo tanto, podemos eliminarlo.
La situación es análoga si procesamos el patrón X-Wing con alas desde el punto de vista de las columnas tercera y octava, en la que podremos eliminar el candidato 5 de la casilla en naranja.
Ahora diseñemos un algoritmo para localizar patrones X-Wing con alas.
Para el caso de filas, buscaremos una fila con solo dos casillas para un candidato. Una vez localizada, buscaremos en el resto de filas otra en las que el candidato aparezca en las mismas columnas, independientemente de que haya otras casillas con el mismo candidato en la misma fila. Las casillas extra con el candidato deben cumplir una condición: que estén en la misma caja que una de las dos casillas que forman el patrón X-Wing.
Las alas solo pueden aparecer en una de las cajas. Si hubiera alas en las dos cajas no tenemos un patrón X-Wing con alas válido.
Hay que tener presente que un patrón X-Wing con alas puede tener una o dos alas en cada caja. El ejemplo que estamos usando contiene un patrón X-Wing con alas simple, pero hay patrones con dos alas, o con un ala larga, en las que las dos casillas restantes de la caja en la misma fila o columna pueden contener el candidato. (En nuestro ejemplo, si el candidato 5 apareciese también en la casilla de la tercera fila y segunda columna). En ese caso hay un tercer supuesto, pero las casillas con candidatos eliminados son las mismas.
Una vez localizado el patrón, eliminaremos como candidato el valor común en el resto de casillas de la caja y columna en que se encuentre el ala o las alas. Por lo tanto, la información mínima que necesitamos para aplicar ésta técnica es la columna y caja de la casilla correspondiente al patrón X-Wing que tiene el o las alas, o más sencillamente, la casilla que contiene alas.
El razonamiento es análogo para patrones X-Wing con alas por columnas.
Añadiremos algunas funciones más a la clase Tablero:
class Tablero {
private:
...
bool BuscaXWingAlasFilas(int v);
bool BuscaXWingAlasColumnas(int v);
bool ProcesaXWingAlasFilas(Pareja par, Casilla *f2, int v);
bool ProcesaXWingAlasColumnas(Pareja par, Casilla *c2, int v);
public:
...
bool ProcesaXWingAlas();
...
};
Para buscar patrones X-Wing con alas usaremos una función para filas y otra análoga para las columnas:
bool Tablero::BuscaXWingAlasFilas(int v) {
bool retval = false;
Pareja par;
for(int f=0; f<9; f++) {
// Detectar fila con dos casillas con el candidato v
par = fila[f].DobleCandidato(v);
// Si par.Cas(0) != NULL, y la pareja no está en la misma caja
// tenemos un candidato a X-Wing con alas, buscaremos en el resto de filas
if(par.Cas(0) != NULL && par.Cas(0)->Caja() != par.Cas(1)->Caja()) {
for(int f2=0; f2<9; f2++) {
// No nos interesa que la segunda fila esté en la misma fila de cajas que la primera
if(f/3 != f2/3) {
Casilla *c2 = fila[f2].DobleCandidatoYMas(par, v);
if(c2) {
retval |= ProcesaXWingAlasFilas(par, c2, v);
}
}
}
}
}
return retval;
}
Necesitamos añadir un método a la clase Fila que busca dos casillas en que un valor que aparezca como candidato y que aparezca también en alguna casilla extra de la misma fila en la misma caja que una de las casillas. Es decir, una fila que cumpla el patrón X-Wing con alas. Para la clase Columna necesitaremos un método análogo.
class Fila {
private:
...
public:
...
Casilla *DobleCandidatoYMas(Pareja par, int v);
};
Y la implementación es algo asi:
Casilla *Fila::DobleCandidatoYMas(Pareja par, int v) {
bool presA, presB, presC;
int c1, c2;
c1 = par.Cas(0)->Columna();
c2 = par.Cas(1)->Columna();
// Verificamos si la las columnas de la pareja par tienen el candidato v
if(cas[c1]->Lapiz().ContieneMarca(v) && cas[c2]->Lapiz().ContieneMarca(v)) {
// Verificamos si el candidato esta presente en una o dos casillas de la misma fila y caja
// De cada una de las columnas.
presA = presB = presC = false;
for(int c=0; c<9; c++) {
// Si la casilla contiene el candidato, pero no forma parte del X-Wing
if(c!=c1 && c!=c2 && cas[c]->Lapiz().ContieneMarca(v)) {
if(cas[c]->Caja() == cas[c1]->Caja()) presA = true; // Es un ala de par(0)
else
if(cas[c]->Caja() == cas[c2]->Caja()) presB = true; // Es un ala de par(1)
else presC = true; // Presencia en caja diferente
}
}
// Si solo hay alas en par(0) o par(1) retornamos la caja a la que pertenecen el o las alas
if(presC) return NULL;
if(presA && !presB) return cas[c1];
if(!presA && presB) return cas[c2];
}
return NULL;
}
Por último, si localizamos un patrón X-Wing con alas, lo procesaremos usando la función correspondiente, que eliminará las marcas de lápiz en la caja en que aparezcan las alas en la misma columna que el patrón X-Wing, o con la función análoga para patrones X-Wing con alas en columnas:
bool Tablero::ProcesaXWingAlasFilas(Pareja par, Casilla *c2, int v) {
bool retval = false;
char cad[100];
// Eliminar el candidato si está presente en la caja y columna de c2, salvo en c2
for(int f=0; f<9; f++) {
retval |= columna[c2->Columna()].Cas(f) != c2 && // No mirar en la casilla c2
columna[c2->Columna()].Cas(f)->Caja() == c2->Caja() && // En la misma caja que c2
columna[c2->Columna()].Cas(f)->Lapiz().EliminaMarca(v)); // Y contiene el candidato v
}
return retval;
}
Solo nos queda procesar todo el tablero buscando patrones X-Wing con alas:
bool Tablero::ProcesaXWingAlas() {
bool retval = false;
for(int v=1; v<=9; v++) {
// Empezamos con las filas.
retval |= BuscaXWingAlasFilas(v);
// Y ahora las columnas.
retval |= BuscaXWingAlasColumnas(v);
}
return retval;
}
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku9 | sudoku9.zip | 2022-06-22 | 25954 bytes | 615 |