Resolución de sudokus (5)
Marcas de lápiz y parejas y trios punteros.
Marcas de lápiz
A partir de aquí será necesario hacer todas las marcas de lápiz en todas las casillas. Una vez hecho eso podemos volver a aplicar algunos métodos conocidos, como el de parejas desnudas, ya que puede que aparezcan algunas que no se habían revelado con los métodos anteriores.
Probablemente también tengamos que acudir a otras técnicas, más avanzadas, empezando por ampliar la técnica de parejas a trios y cuartetos.
Todas las técnicas avanzadas que veremos a partir de ahora están destinadas a eliminar marcas de lápiz, que indirectamente nos llevarán a la solución, con suerte.
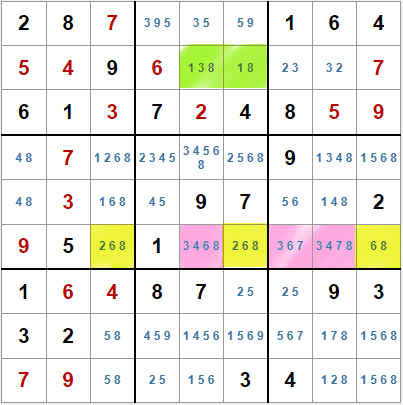
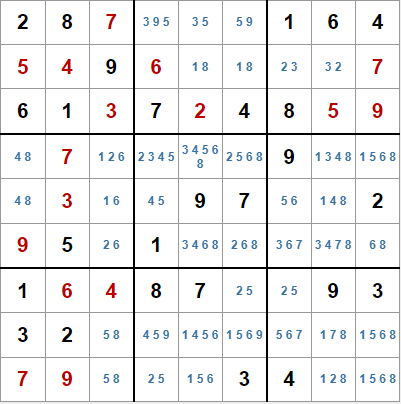
Para empezar añadiremos las marcas de lápiz, sin tener en cuenta las parejas y trios punteros que ya conocíamos por ahora, y vemos algunas situaciones nuevas en el tablero:
- En la segunda línea, el par desnudo 1,8 de las casillas quinta y sexta ha quedado oculto. Ya habíamos descubierto este par desnudo antes, pero al igual que ahora éste ha quedado oculto, al marcar todos los candidatos pueden aparecer otros pares ocultos. No es el caso de este sudoku, pero trabajaremos en un algoritmo para descubrir estos pares ocultos.
- En la sexta fila tenemos, en amarillo, un trio desnudo en las casillas tercera, sexta y novena, con los valores 2, 6 y 8. Esto descarta esos tres valores del resto de casillas de esa fila. En rosa, si eliminamos esos valores, quedaría otro trio desnudo, con los valores 3, 4 y 7,
El método para añadir las marcas y procesar las parejas y trios punteros sería algo así:
void Tablero::PonerMarcasLapiz() {
// Para cada casilla colocar marcas de lápiz que faltan:
for(int f=0; f<9; f++) {
for(int c=0; c<9; c++) {
if(!casilla[f][c].Valor()) { // Si no tiene un valor asignado
for(int v=1; v<=9; v++) {
int k = casilla[f][c].Caja();
if(!fila[f].Presente(v) && !columna[c].Presente(v) && !caja[k].Presente(v))
casilla[f][c].MarcaLapiz(v);
}
}
}
}
for(int v=1; v<=9; v++) { // Para cada posible valor
int ncaja=0;
for(int f=0; f<3; f++) { // Fila de cajas
for(int c=0; c<3; c++) { // Columna de cajas
for(int i=0; i<3; i++) { // Fila de punteros
if(caja[ncaja].PunteroFila(i, v)) fila[f*3+i].DesmarcaLapizMenosCaja(c, v);
}
for(int i=0; i<3; i++) { // Columna de punteros
if(caja[ncaja].PunteroColumna(i, v)) columna[c*3+i].DesmarcaLapizMenosCaja(f, v);
}
ncaja++;
}
}
}
}
Hemos añadido el método DesmarcaLapizMenosCaja a las clases Fila y Columna, para quitar las marcas a las casillas afectadas por las parejas y trios puntero.
void Fila::DesmarcaLapizMenosCaja(int k, int v) {
for(int i=0; i<9; i++)
if(i/3 != k) cas[i]->DesmarcaLapiz(v);
}
Casillas con solo una marca de lápiz
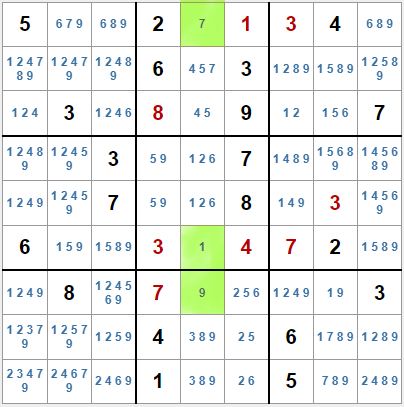
Al aplicar los métodos de resolución que veamos a partir de ahora se irán eliminando candidatos en ciertas casillas. Como resultado, en alguna casilla puede quedar una única marca de lápiz. Evidentemente, esa marca de lápiz es el valor de la casilla, así que podemos asignarlo.
El sudoku del ejemplo de la izquierda hemos colocado todas las marcas de lápiz, y vemos que en la quinta columna hay tres casillas, resaltadas en verde, que solo tienen una marca de lápiz.
Crearemos un método en la clase Tablero para esta tarea y lo invocaremos después de aplicar cada uno de los métodos que iremos desarrollando.
Esto es importante por dos motivos:
- Es la forma intuitiva de resolver el sudoku, cuando los resolvemos nosotros, si en una casilla solo queda una marca de lápiz, automáticamente colocaremos el valor final.
- Algunos algoritmos que veremos más adelante no funcionarán bien (o serán más complicados de programar) si en algunas casillas solo hay una marca de lápiz en lugar de un valor final.
bool Tablero::CasillasConUnaMarcaLapiz() {
bool retval=false;
int v;
for(int f=0; f<9; f++) {
for(int c=0; c<9; c++) {
if(casilla[f][c].NumeroMarcasLapiz() == 1) {
retval = true;
v=1;
while(!casilla[f][c].Lapiz(v)) v++;
Asignar(f, c, v);
}
}
}
return retval;
}
Zonas con un candidato en una única casilla
Ya tuvimos en cuenta esta situación en la fase 1, pero en la fase 2 no la estamos haciendo.
Existe la posibilidad que al ir eliminando candidatos de las casillas, en una fila, columna o caja un candidato concreto solo aparezca en una casilla.
No confundir con el caso anterior, en esa casilla puede haber otros candidatos, pero el que nos ocupa solo aparece en esa, y por lo tanto, también es un valor final.
Añadiremos una función a las clases Fila, Columna y Caja para buscar esas casillas con el único candidato:
class Fila {
...
public:
...
Unico UnicaCasillaConCandidato();
...
};
La definición es la misma para las tres clases:
Unico Fila::UnicaCasillaConCandidato() {
Unico u(-1, 0);
int cuenta;
for(int v=1; v<=9; v++) {
cuenta = 0;
for(int c=0; c<9; c++) {
if(!cas[c]->Valor()) {
if(cas[c]->Lapiz(v)) {
u = Unico(c, v);
cuenta++;
}
}
}
if(cuenta==1) return u;
}
return Unico(-1, 0);
}
En la clase Tablero añadiremos una función para buscar esas casillas en cada fila, columna y caja:
class Tablero {
private:
...
public:
...
bool UnicaCasillaConCandidato();
...
};
Y la definición es:
bool Tablero::UnicaCasillaConCandidato() {
bool retval = false;
Unico u(0,0);
// Buscar casillas con único valor de candidato en filas, columnas y cajas:
for(int f=0; f<9; f++) {
u = fila[f].UnicaCasillaConCandidato();
if(u.Casilla() != -1) {
Asignar(f, u.Casilla(), u.Valor());
retval = true;
}
}
for(int c=0; c<9; c++) {
u = columna[c].UnicaCasillaConCandidato();
if(u.Casilla() != -1) {
Asignar(u.Casilla(), c, u.Valor());
retval = true;
}
}
for(int k=0; k<9; k++) {
u = caja[k].UnicaCasillaConCandidato();
if(u.Casilla() != -1) {
int fil = caja[k].Cas(u.Casilla())->Fila();
int col = caja[k].Cas(u.Casilla())->Columna();
Asignar(fil, col, u.Valor());
retval = true;
}
}
return retval;
}
Valores finales
Debido a que deberemos invocar estos dos procedimientos cada vez que apliquemos un método que elimine candidatos de alguna casilla, será útil combinarlos en uno solo.
Añadiremos un nuevo método VerificarFinales a la clase Tablero:
class Tablero {
private:
...
public:
...
bool VerificarFinales();
...
};
Que simplemente llama a los dos métodos anteriores:
bool Tablero::VerificarFinales() {
bool retval=false;
while(CasillasConUnaMarcaLapiz()) {
retval = true;
}
while(UnicaCasillaConCandidato()) {
retval = true;
}
return retval;
}
Procesar pares desnudos
Al entrar en la fase 2 ya no se volverán a procesar los métodos de la fase 1, ya que estarán en un bucle independiente. Sin embargo, procesar los pares desnudos en la segunda fase aún puede aportar información, eliminando candidatos de algunas casillas.
El método para localizar pares desnudos sigue siendo válido, pero crearemos métodos alternativos para procesarlos en la segunda fase, más simples que los de la fase 1:
class Tablero {
private:
...
bool ProcesaParesDesnudosFilaFase2(int f);
bool ProcesaParesDesnudosColumnaFase2(int c);
bool ProcesaParesDesnudosCajaFase2(int c);
...
public:
...
bool ProcesaParesDesnudosFase2();
...
};
Para las filas, el método es:
bool Tablero::ProcesaParesDesnudosFilaFase2(int f) {
bool retval = false;
// Procesar pares desnudos
ListaDesnudo()->Primero();
while(ListaDesnudo()->Actual()) {
int fil = ListaDesnudo()->ValorActual().MismaFila();
if(fil == f) {
for(int c=0; c<9; c++) {
if(c != ListaDesnudo()->ValorActual().Cas(0)->Columna() &&
c != ListaDesnudo()->ValorActual().Cas(1)->Columna() &&
(!ListaDesnudo()->ValorActual().Trio() || c!= ListaDesnudo()->ValorActual().Cas(2)->Columna())) {
retval |= casilla[f][c].DesmarcaLapiz(ListaDesnudo()->ValorActual().Val(0));
retval |= casilla[f][c].DesmarcaLapiz(ListaDesnudo()->ValorActual().Val(1));
}
}
}
ListaDesnudo()->Siguiente();
}
return retval;
}
Para las columnas y cajas las funciones son parecidas.
Parejas y trios puntero
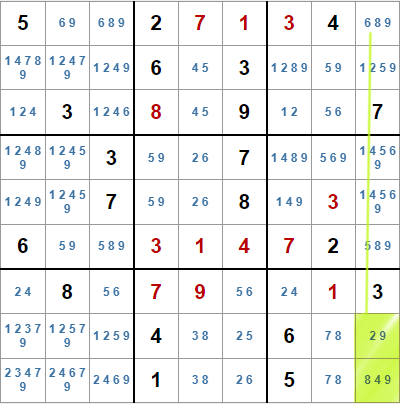
Una vez hemos colocado todas las marcas de lápiz, los métodos anteriores ya no nos sirven para seguir resolviendo el sudoku, por lo que perderemos información sobre las parejas y trios puntero que teníamos en la fase uno. Así que añadiremos nuevos métodos para localizar y procesar esa información.
En el ejemplo de la derecha, en la novena caja tenemos un par puntero formado por dos 9 que sólo aparecen en dos casillas de la misma columna de esa caja. Esto nos permite eliminar como candidato los 9 en la novena columna de las cajas tercera y sexta.
Ya no usaremos las mismas estructuras que en la fase uno.
Aunque podríamos usar la lista de pares y trios desnudos para almacenar también los pares y trios puntero, por claridad, crearemos otra clase 'Puntero", y añadiremos una lista de estos elementos a la clase Tablero.
class Puntero {
private:
int elementos;
Casilla *cas[3];
int val;
public:
Puntero(int n=0) : elementos(n) {
cas[0] = cas[1] = cas[2] = NULL;
}
void AsignarCas(int pos, Casilla *c) { cas[pos] = c; }
void AsignarVal(int v) { val = v; }
bool Par() const { return elementos==2; }
bool Trio() const { return elementos==3; }
Casilla *Cas(int c) { return cas[c]; }
int Val() { return val; }
bool operator<(const Puntero &d) const;
bool operator==(const Puntero &d) const;
int MismaFila();
int MismaColumna();
int MismaCaja();
};
Esta clase es casi idéntica a la clase 'Desnudo', salvo porque solo almacenamos un valor, ya que los punteros solo tienen uno.
Para que consideremos que ciertas casillas forman un par o trio puntero tienen que cumplir ciertas condiciones:
- Deben estar formadas por dos o tres casillas con una marca de lápiz común.
- Todas las casillas deben estar en la misma fila o columna y en la misma caja.
No consideraremos un par o trio puntero casillas que, aún estando en la misma fila o columna, ocupen más de una caja.
Añadiremos algunos métodos privados y uno público para buscar punteros, así como un método para obtener una referencia a la lista de punteros:
class Tablero {
private:
...
Lista<Puntero> puntero;
...
bool BuscaPunterosFila(int f, int v);
bool BuscaPunterosColumna(int c, int v);
bool BuscaPunterosCaja(int k, int v);
public:
...
Lista<Puntero> *ListaPuntero() { return &puntero; }
...
bool BuscaPunteros();
...
};
Para detectar estos punteros usaremos un método para filas, otro para columnas y un tercero para cajas.
bool Tablero::BuscaPunterosFila(int f, int v) {
int cuenta = 0;
// Si el valor v está asignado a la fila, retornar false
if(!fila[f].Presente(v)) {
// Leer casillas con la marca de lápiz v. Si son más de tres retornar false
for(int c=0; c<9; c++) if(fila[f].Cas(c)->Lapiz(v)) cuenta++;
if(cuenta == 3 || cuenta == 2) {
Puntero pun(cuenta);
cuenta = 0;
pun.AsignarVal(v);
for(int c=0; c<9; c++) {
if(fila[f].Cas(c)->Lapiz(v)) {
pun.AsignarCas(cuenta++, fila[f].Cas(c));
}
}
// Si todas las casillas están en la misma caja, almacenar.
if(pun.MismaCaja()!=-1) {
puntero.Insertar(pun);
return true;
}
}
}
return false;
}
Las funciones para buscar punteros en columnas y cajas son análogas.
Para buscar todos los punteros usaremos el método BuscaPunteros.
bool Tablero::BuscaPunteros() {
bool retval = false;
for(int v=1; v<=9; v++) {
for(int f=0; f<9; f++)
retval |= BuscaPunterosFila(f, v);
for(int c=0; c<9; c++)
retval |= BuscaPunterosColumna(c, v);
for(int k=0; k<9; k++)
retval |= BuscaPunterosCaja(k, v);
}
return retval;
}
Un puntero detectado en una fila o columna puede eliminar marcas de lápiz en la caja en la que se encuentre. Un puntero detectado en una caja puede eliminar marcas de lápiz en la fila o columna en la que se encuentre.
Una vez detectados todos los punteros ya podemos procesarlos.
Para ello añadiremos otros tres métodos privados, para procesar los punteros por filas, columnas y cajas, y un cuarto público para procesarlos todos.
class Tablero {
private:
...
bool ProcesaPunterosFila(int f);
bool ProcesaPunterosColumna(int c);
bool ProcesaPunterosCaja(int k);
...
public:
...
bool ProcesaPunteros();
...
};
bool Tablero::ProcesaPunterosFila(int f) {
bool retval = false;
// Procesar punteros
ListaPuntero()->Primero();
while(ListaPuntero()->Actual()) {
int fil = ListaPuntero()->ValorActual().MismaFila();
if(fil == f) {
for(int c=0; c<9; c++) {
if(c != ListaPuntero()->ValorActual().Cas(0)->Columna() &&
c != ListaPuntero()->ValorActual().Cas(1)->Columna() &&
(!ListaPuntero()->ValorActual().Trio() || c!= ListaPuntero()->ValorActual().Cas(2)->Columna())) {
retval |= casilla[f][c].DesmarcaLapiz(ListaPuntero()->ValorActual().Val());
}
}
}
ListaPuntero()->Siguiente();
}
return retval;
}
De nuevo, para columnas y cajas los métodos son análogos.
El método para procesar todos los punteros es simple:
bool Tablero::ProcesaPunteros() {
bool retval = false;
for(int f=0; f<9; f++) retval |= ProcesaPunterosFila(f);
for(int c=0; c<9; c++) retval |= ProcesaPunterosColumna(c);
for(int k=0; k<9; k++) retval |= ProcesaPunterosCaja(k);
return retval;
}
Bucle de resolución
Nuestro bucle para procesar cada método de resolución queda ahora dividido en dos bucles. Uno para la fase 1, que es el que usábamos en el programa del capítulo anterior, y otro para la fase 2:
do {
// Bucle de fase 1
repetir=false;
...
} while(repetir);
// FASE 2:
T.PonerMarcasLapiz();
T.VerificarFinales();
do {
repetir=false;
T.BuscaParesDesnudos();
if(T.ProcesaParesDesnudosFase2()) {
repetir =true;
T.VerificarFinales();
}
T.BuscaPunteros();
if(!repetir && T.ProcesaPunteros()) {
repetir =true;
T.VerificarFinales();
}
} while(repetir);
...
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku5 | sudoku5.zip | 2022-06-22 | 18287 bytes | 624 |