Resolución de sudokus (4)
Parejas desnudas.
Pares desnudos
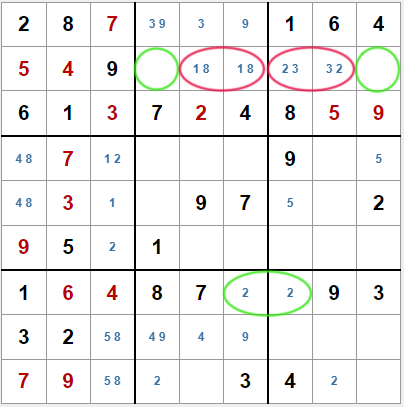
Veamos otro sudoku parcialmente solucionado con las técnicas que hemos incorporado hasta ahora, y fijémonos en la segunda fila.
Tenemos seis casillas libres, y faltan los valores 1, 2, 3, 6, 7 y 8. Pero el 1 y el 8 solo pueden estar en las casillas quinta y sexta, y el 2 y 3 en las casillas séptima y octava. Esto implica que en las otras dos casillas solo pueden estar los valores 6 y 7. Es decir, podemos marcar a lápiz un tercer par de valores. Aunque en realidad, en la cuarta casilla solo puede estar el 6 y en la novena el 7.
A estas parejas de candidatos en parejas de casillas se les suele denominar "pares desnudos". Nuestro objetivo ahora es localizarlas y aprovechar la información que que aportan a la solución.
Tenemos un caso parecido en la séptima fila. Solo hay dos casillas libres, y faltan los valores 2 y 5, por lo que podremos añadir a lápiz el 5 en ambas casillas.
Cuando hagamos las cribas, estos pares también se comportan como pares punteros, aunque estén en cajas diferentes. Sin embargo esta información es redundante en esta fase de la resolución.
También existen trios, cuartetos, quintetos, sextetos y hasta septetos desnudos, pero localizarlos no es tan sencillo, y los trataremos en otro capítulo.
A la hora de resolver este problema, podríamos plantearnos almacenar los pares desnudos en un array, en el caso límite, dado que cada fila, columna y caja tiene nueve casillas, habrá cuatro pares desnudos. Hay 9 filas, 9 columnas y 9 cajas, así que en un sudoku el número de parejas desnudas sería como máximo 4x9x3, es decir, 108 (en realidad son bastantes menos, ya que hay casillas con valor inicial, y casillas que no pueden formar parte de parejas). Sin embargo será más eficaz usar una lista enlazada o una estructura vector de stl.
Usaremos como base la plantilla de lista abierta del curso de estructuras dinámicas de datos, y la modificaremos mínimamente para evitar que se puedan añadir nodos repetidos, y para que el método de inserción devuelva un valor true si se añade el nuevo elemento o false si ya existía en la lista, al tiempo que el puntero actual apunte a ese elemento.
Esto es necesario porque la misma pareja en una fila o columna, también puede estar en una caja, y el procedimiento para procesar estas pares desnudos no funcionará bien si se procesa dos veces alguno de ellos.
Necesitaremos algunos métodos auxiliares, por ejemplo, para saber cuántas casillas quedan libres en una fila, columna o caja, teniendo en cuenta las parejas desnudas que conocemos.
Necesitamos una clase para almacenar parejas desnudas (y posteriormente otros grupos).
También nos harán falta funciones que nos indiquen si las casillas de un par desnudo pertenecen a la misma fila, columna o caja.
Por otra parte, nuestras clases empiezan a ser algo complejas, de modo que las separaremos en varios ficheros, creando para cada una un fichero de declaración y otro de definición.
// (C) 2022 Salvador Pozo
// Con Clase https://conclase.net
//
// Declaración de la clase Desnudo
#ifndef SUDOKU_DESNUDO
#define SUDOKU_DESNUDO
#include "casilla.h"
class Desnudo {
private:
int elementos;
bool paraBorrar;
Casilla *cas[3];
int val[3];
public:
Desnudo(int n=0) : elementos(n) {
cas[0] = cas[1] = cas[2] = NULL;
}
void AsignarCas(int pos, Casilla *c) { cas[pos] = c; }
void AsignarVal(int pos, int v) { val[pos] = v; }
bool Par() const { return elementos==2; }
bool Trio() const { return elementos==3; }
Casilla *Cas(int c) { return cas[c]; }
int Val(int n) { return val[n]; }
bool operator<(const Desnudo &d) const;
bool operator==(const Desnudo &d) const;
void MarcarParaBorrar() { paraBorrar = true; }
void MarcarParaNoBorrar() { paraBorrar = false; }
bool MarcadoParaBorrar() const { return paraBorrar; }
int MismaFila();
int MismaColumna();
int MismaCaja();
};
#endif // SUDOKU_DESNUDO
Aunque esta clase puede manejar trios desnudos, de momento solo procesaremos pares.
Añadiremos una lista enlazada de objetos Desnudo a la clase Tablero, y los procedimientos para buscar pares desnudos:
class Tablero {
private:
...
Lista<Desnudo> desnudo;
bool BuscaParesDesnudosFila(int f);
bool BuscaParesDesnudosColumna(int c);
bool BuscaParesDesnudosCaja(int c);
bool ProcesaParesDesnudosFila(int f);
bool ProcesaParesDesnudosColumna(int c);
bool ProcesaParesDesnudosCaja(int c);
public:
...
bool BuscaParesDesnudos();
bool ProcesaParesDesnudos();
Lista<Desnudo> *ListaDesnudo() { return &desnudo; }
};
La función para buscar pares desnudos en una fila o columna son muy parecidas:
bool Tablero::BuscaParesDesnudosFila(int f) {
int cuenta, coincidencia;
Desnudo des(2);
bool retval = false;
for(int i=0; i<8; i++) {
// Solo buscamos en casillas vacías con dos marcas de lápiz.
if(casilla[f][i].Valor() == 0 && casilla[f][i].NumeroMarcasLapiz() == 2) {
cuenta = coincidencia = 0;
des.AsignarCas(0, &casilla[f][i]);
for(int l=1; l<=9; l++) {
if(casilla[f][i].Lapiz(l)) {
des.AsignarVal(cuenta, l);
cuenta++;
}
}
if(cuenta==2) { // con dos valores posibles
for(int k=i+1; k<9; k++) {
// Buscamos en el resto de casillas vacías con dos valores posibles
if(casilla[f][k].Valor() == 0 && casilla[f][k].NumeroMarcasLapiz() == 2) {
cuenta = 0;
des.AsignarCas(1, &casilla[f][k]);
for(int l=1; l<=9; l++) {
if(casilla[f][k].Lapiz(l) && des.Val(cuenta) == l) {
coincidencia++;
cuenta++;
}
}
}
if(cuenta==2 && coincidencia==2) {
retval = true;
if(desnudo.InsertarFinal(des))
i++;
} else {
desnudo.ValorActual().MarcarParaNoBorrar();
}
}
break;
}
}
}
}
return retval;
}
También buscaremos pares desnudos en columnas y cajas.
La idea es simple:
- Buscamos una casilla libre con dos marcas de lápiz.
- Si la encontramos, buscamos en el resto de casillas libres una con las mismas marcas de lápiz.
- Si también la encontramos, almacenamos la pareja desnuda.
- Continuamos a partir de la siguiente casilla.
Hay que buscar y añadir los pares desnudos localizados en cada fila, columna y caja. Para ello usaremos el método público BuscaParesDesnudos de la clase Tablero:
bool Tablero::BuscaParesDesnudos() {
bool retval=false;
// Marcar todos los elementos para borrar:
for(ListaDesnudo()->Primero(); ListaDesnudo()->Actual(); ListaDesnudo()->Siguiente())
ListaDesnudo()->ValorActual().MarcarParaBorrar();
for(int f=0; f<9; f++) {
retval |= BuscaParesDesnudosFila(f);
}
for(int c=0; c<9; c++) {
retval |= BuscaParesDesnudosColumna(c);
}
for(int k=0; k<9; k++) {
retval |= BuscaParesDesnudosCaja(k);
}
// Eliminar elementos marcados para borrar:
for(ListaDesnudo()->Primero(); ListaDesnudo()->Actual(); ListaDesnudo()->Siguiente())
if(ListaDesnudo()->ValorActual().MarcadoParaBorrar()) ListaDesnudo()->BorrarActual();
return retval;
}
Para poder generar un fichero de salida con las instrucciones para resolver el sudoku nos interesa que no se repita cada vez que se detecta el mismo par desnudo. Ya que en cada iteración de este método algunos pares desnudos detectados en la anterior iteración seguirán existiendo, hemos incorporado una marca en cada elemento de la lista que nos permite detectar si el par desnudo detectado es nuevo o no. Si un par detectado ya estaba en la lista, simplemente lo marcaremos para que no sea borrado, pero no lo tendremos en cuenta para generar las instrucciones en el fichero de salida. Al finalizar el procedimiento de búsqueda eliminaremos los pares desnudos que ya no estén en el tablero.
Nota: en realidad, si un par desnudo detectado en una iteración anterior ya no se detecta después, la información que pueda aportar es redundante. Un par desnudo solo aporta información para la fila, columna o caja en la que se encuentre, pero si ya no es detectado es porque esas casillas tienen ahora un valor final, y eso aporta información adicional, pero no contradice a la que aportaba el par desnudo. De modo que, en rigor, no sería necesario eliminar esos elementos de la lista de pares desnudos.
Solo nos queda procesar la nueva información.
Para cada fila, columna y caja eliminaremos como candidatos los valores de las casillas con valor y los correspondientes pares desnudos. Si sólo nos quedan dos valores para dos casillas, añadiremos otro par desnudo y las marcas de lápiz correspondientes.
bool Tablero::ProcesaParesDesnudosFila(int f) {
bool retval = false;
bool presente[9] = { false, false, false, false, false, false, false, false, false };
bool caslibre[9];
int lapiz[2] = { 0, 0 };
int libre[2] = { 0, 0 };
int libres=9, fil;
for(int c=0; c<9; c++) {
caslibre[c] = !casilla[f][c].Valor();
if(!caslibre[c]) {
presente[casilla[f][c].Valor()-1] = true;
libres--;
}
}
// Procesar pares desnudos
ListaDesnudo()->Primero();
while(ListaDesnudo()->Actual()) {
fil = ListaDesnudo()->ValorActual().MismaFila();
if(fil == f) {
caslibre[ListaDesnudo()->ValorActual().Cas(0)->Columna()] = false;
caslibre[ListaDesnudo()->ValorActual().Cas(1)->Columna()] = false;
libres -= 2;
presente[ListaDesnudo()->ValorActual().Val(0)-1] = true;
presente[ListaDesnudo()->ValorActual().Val(1)-1] = true;
}
ListaDesnudo()->Siguiente();
}
if(libres==2) { // Nuevo par desnudo
// Obtener los dos valores del nuevo par:
for(int i=0,v=1; v<=9; v++) {
if(!presente[v-1]) lapiz[i++]=v;
}
for(int i=0,c=0; c<9; c++) {
if(caslibre[c]) libre[i++]=c;
}
// En cada casilla libre marcar a lápiz los valores no presentes
int k0 = casilla[f][libre[0]].Caja();
int k1 = casilla[f][libre[1]].Caja();
if(!casilla[f][libre[0]].Valor()) {
retval |= casilla[f][libre[0]].MarcaLapiz(lapiz[0]);
retval |= casilla[f][libre[0]].MarcaLapiz(lapiz[1]);
}
if(!casilla[f][libre[1]].Valor()) {
retval |= casilla[f][libre[1]].MarcaLapiz(lapiz[0]);
retval |= casilla[f][libre[1]].MarcaLapiz(lapiz[1]);
}
if(columna[libre[0]].Presente(lapiz[0]) || caja[k0].Presente(lapiz[0])) {
Asignar(f, libre[0], lapiz[1]);
retval=true;
} else
if(columna[libre[0]].Presente(lapiz[1]) || caja[k0].Presente(lapiz[1])) {
Asignar(f, libre[0], lapiz[0]);
retval=true;
}
if(columna[libre[1]].Presente(lapiz[0]) || caja[k1].Presente(lapiz[0])) {
Asignar(f, libre[1], lapiz[1]);
retval=true;
} else
if(columna[libre[1]].Presente(lapiz[1]) || caja[k1].Presente(lapiz[1])) {
Asignar(f, libre[1], lapiz[0]);
retval=true;
}
}
return retval;
}
La función pública de Tablero ProcesaParesDesnudos se encargará de procesar todos los pares detectados para cada fila, columna y caja:
bool Tablero::ProcesaParesDesnudos() {
bool retval = false;
for(int f=0; f<9; f++) retval |= ProcesaParesDesnudosFila(f);
for(int c=0; c<9; c++) retval |= ProcesaParesDesnudosColumna(c);
for(int k=0; k<9; k++) retval |= ProcesaParesDesnudosCaja(k);
return retval;
}
Bucle de resolución
Finalmente, en nuestra función main, añadimos las llamadas necesarias para procesar pares desnudos:
do {
repetir=false;
...
if(!repetir) {
T.BuscaParesDesnudos();
if(T.ProcesaParesDesnudos()) {
repetir = true;
}
}
} while(repetir);
Este método solo se usará si ninguno de los anteriores aporta nueva información. Esto posteriormente nos permitirá asignar una dificultad diferente si para solucionar el sudoku hemos tenido que recurrir a este método para resolverlo.
Aunque aplicar el proceso de pares desnudos para este sudoku en particular solo ha desvelado un par de casillas y un par de parejas puntero, puede ser la solución para otros sudokus, y aporta información importante para aplicar otros métodos.
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku4 | sudoku4.zip | 2022-06-22 | 14930 bytes | 732 |