Resolución de sudokus (3)

Candidatos únicos y solitarios.

Filas, columnas o cajas con candidato único

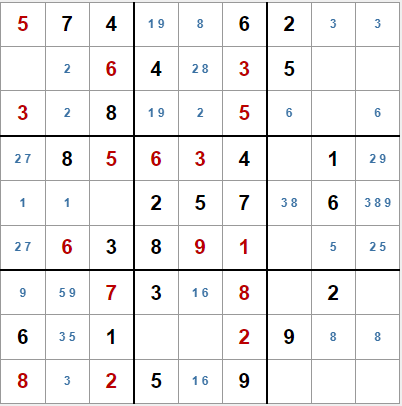
Otra técnica que podemos considerar básica es localizar filas, columnas o cajas con un único candidato posible.

Fijémonos en la tercera columna, en la que sólo hay una casilla libre, y el único valor que falta es el 9. Esto nos proporciona algunos valores adicionales.

Añadiremos una nueva clase Unico para almacenar una casilla y su valor:

class Unico {
    private:
    int casilla;
    int valor;
    public:
    Unico(int c, int v) : casilla(c), valor(v) {}
    int Casilla() { return casilla; }
    int Valor() { return valor; }
};

Y añadiremos un método a las clases Fila, Columna y Caja para localizar candidatos únicos:

Unico Fila::CandidatoUnico() {
    bool valor[9] = {false, false, false, false, false, false, false, false, false};
    int cuenta = 0;
    int i, c;

    // Contar valores, si son 8 devolver valor que falta:
    for(i=0; i<9; i++) {
        if(cas[i]->Valor()) {
            cuenta++;
            valor[cas[i]->Valor()-1] = true;
        } else
            c=i;
    }
    if(cuenta == 8) {
        i=0;
        while(valor[i++]);
        return Unico(c, i);
    }
    return Unico(-1,0);
}

Los tres métodos son similares.

Por último, añadiremos un método a Tablero y lo invocaremos en cada bucle:

bool Tablero::CandidatoUnico() {
    bool retval = false;
    Unico u(0,0);

    // Buscar candidatos únicos en filas, columnas y cajas:
    for(int f=0; f<9; f++) {
        u = fila[f].CandidatoUnico();
        if(u.Casilla() != -1) {
            Asignar(f, u.Casilla(), u.Valor());
            retval = true;
        }
    }

    for(int c=0; c<9; c++) {
        u = columna[c].CandidatoUnico();
        if(u.Casilla() != -1) {
            Asignar(u.Casilla(), c, u.Valor());
            retval = true;
        }
    }

    for(int i=0; i<9; i++) {
        u = caja[i].CandidatoUnico();
        if(u.Casilla() != -1) {
            Asignar(caja[i].Cas(u.Casilla())->Fila(), caja[i].Cas(u.Casilla())->Columna(), u.Valor());
            retval = true;
        }
    }
    return retval;
}

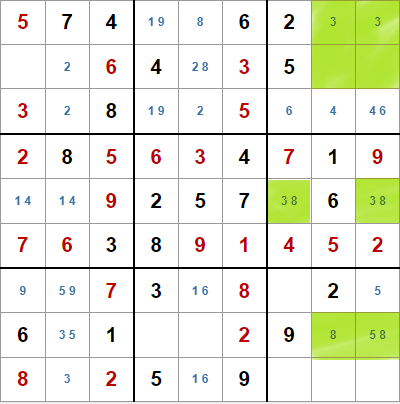
Con ésta nueva técnica el resultado es el de la derecha.

Candidatos solitarios

Necesitamos otro método. Fijémonos ahora en los 8 de la tercera columna de cajas. En la tercera caja solo se puede colocar el 8 en las casillas de las columnas octava y novena de las dos primera filas. En la novena caja solo en las columnas octava y novena de la segunda caja. Para la séptima columna solo es posible colocar un 8 en la sexta caja. Esto es más evidente viendo la criba.

Diseñemos un algoritmo para esta técnica. Para cada fila y columna procesaremos el resultado de la criba buscando aquellas que solo tengan una casilla posible. Para ello añadiremos un método a las clases Fila y Columna:

int Fila::UnicoPosible() {
    int cuenta=0;
    int pos = -1;
    for(int i=0; i<9; i++) {
        if(cas[i]->Posible()) {
            cuenta++;
            pos = i;
        }
    }
    if(cuenta == 1) return pos;
    return -1;
}

Una vez definidos estos métodos, procesar la criba es sencillo:

bool Tablero::ProcesarCribaSolitarios(int v) {
    bool retval = false;
    int fil, col;

    for(int i=0; i<9; i++) { // Verificar cada fila
        col = fila[i].UnicoPosible();
        if(col != -1) {
            Asignar(i, col, v);
            retval = true;
        }
    }

    for(int i=0; i<9; i++) { // Verificar cada columna
        fil = columna[i].UnicoPosible();
        if(fil != -1) {
            Asignar(fil, i, v);
            retval = true;
        }
    }
    return retval;
}

Bucle de resolución

Completamos el bucle con los nuevos métodos. La idea es aplicar cada método solo si los anteriores no consiguen aportar información nueva.

    do {
        repetir=false;
        for(int v=1; v<=9; v++) {
            do {
                T.Criba(v);
                insistir = T.ProcesarCriba(v);
                repetir |= insistir;
            } while(insistir);
        }
        if(!repetir && T.CandidatoUnico()) {
            repetir = true;
        }
        if(!repetir) {
            for(int v=1; v<=9; v++) {
                T.Criba(v);
                repetir |= T.ProcesarCribaSolitarios(v);
            }
        }
    } while(repetir);

Con esto quedaría resuelto este sudoku en concreto, y muchos de los catalogados como de dificultad fácil y media. Pero muchos otros aún se resistirán.