Resolución de sudokus (2)

Criba de casillas.

Tres en raya

Empecemos a implementar algunos métodos de resolución.

El primero se conoce como "tres en raya" o "tic-tac-toe". Trabajaremos con filas y columnas, pero de cajas. Para cada una de esas filas y columnas buscaremos valores que estén presentes en dos de las cajas.

Para cada valor y para cada caja, combinamos la información con las cajas en la misma columna y fila de cajas, de modo que podemos reducir las casillas en las que es posible colocar el valor que estamos analizando.

Para cada caja, en general, pueden darse varios casos, pero nos fijaremos ahora en tres de ellos. Que en la caja en la que no esté presente el valor haya:

Un única casilla en la que colocar el valor: en cuyo caso podremos colocar el valor en esa casilla.
Dos posibles casillas en las que colocarlo: si están en la misma fila o columna tendremos lo que denominamos una pareja puntero.
Tres casillas en las que colocar el valor: si están en la misma fila o columna, tendremos un trio puntero.

Las parejas y trios punteros se comportan como valores finales en la fila o columna en la que aparecen. Es decir, pueden eliminar casillas como candidatas en las cajas de la misma fila o columna en las que se encuentran.

En el resto de casos consideraremos que este método no aporta información útil para resolver el sudoku, en esta fase de la resolución.

En cada uno de los tres casos actuaremos de modo diferente.

En el primero, marcaremos el valor final en la casilla, y repetiremos en análisis para el mismo valor, ya que la nueva información puede descubrir situaciones similares en otras cajas para el mismo valor.
En el segundo caso, añadiremos marcas de lápiz para el valor en las dos casillas. Si además esas casillas forman un par puntero, repetiremos el análisis para el mismo valor.
Para el tercer caso, no añadiremos marcas de lápiz, pero si las tres casillas forman un trio puntero, repetiremos en análisis con el mismo valor.

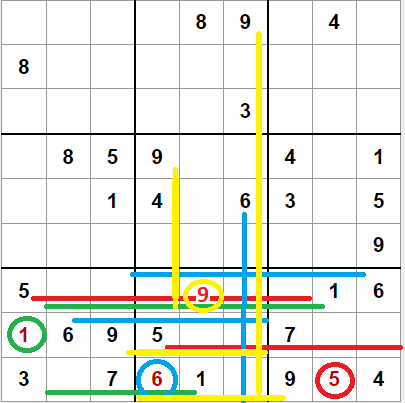
En el ejemplo de la derecha tenemos tres casos para la tercera fila de cajas:

El 1 está presente en la segunda y tercera caja de la fila, y solo deja como posible casilla en la primera caja una casilla, por lo que procedemos a colocar un 1.
El 5 está presente en la primera y segunda caja de la fila, y solo deja como posible casilla en la tercera caja una casilla, por lo que procedemos a colocar un 5.
El 6 está presente en la primera y tercera caja de la fila, y deja dos casillas como posibles en la segunda caja, pero si combinamos con el 6 en la segunda caja de la segunda columna de cajas, podremos eliminar una de esas casillas, por lo que procedemos a colocar un 6 en la otra.
El 9 está presente en la primera y tercera caja de la fila, y deja tres casillas como posibles en la segunda caja, pero si combinamos con los 9 en las primera y segunda cajas de la segunda columna de cajas, podremos eliminar dos de esas casillas, por lo que procedemos a colocar un 9 en la otra.
Por último, los 7 en la primera y segunda caja nos dejan una pareja puntero en la segunda caja. Añadiremos las marcas de lápiz en esas casillas.

Este es el primer método que implementaremos. Si un sudoku se puede resolver usando solo este método lo clasificaremos como muy fácil.

Pero, ¿Cómo trasladaremos cada método a un programa C++?

Empecemos con un método visual y posteriormente pensaremos en el modo de llevarlo a código.

Para cada valor, de 1 a 9, marcaremos todas las casillas donde no puede aparecer ese valor, eso incluye las casillas que ya tengan un valor. Tendremos en cuenta también las parejas y trios puntero a la hora de eliminar casillas.

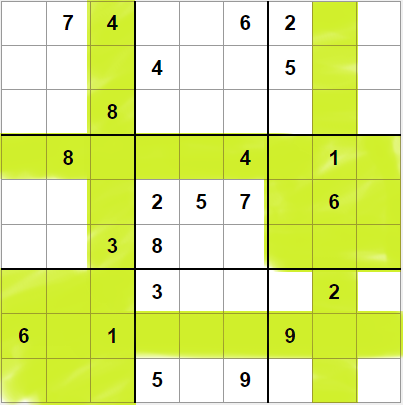
Por ejemplo, en el sudoku de la derecha hemos eliminado las casillas donde no puede aparecer el valor 1. Vemos que en la quinta caja (la central), aparece una pareja puntero en la tercera fila. Eso elimina la tercera fila en la cuarta caja, y revela otra pareja puntero. Las parejas las marcaremos "en lápiz", esto en nuestro programa significa que tendremos que buscar algún modo de almacenar los punteros.

Nuestro programa puede crear un segundo tablero en el que marcaremos las casillas ocupadas y las que no pueden almacenar un valor determinado, en nuestro ejemplo el 1.

Tendremos que diseñar un algoritmo que para cada caja busque casillas únicas, parejas, parejas puntero y trios puntero.

Este algoritmo debe discriminar cajas en las que haya una, dos o tres casillas posibles:

Si solo hay una, se marca valor como final. Esto es información adicional, por lo que podemos repetir el proceso para el mismo valor.
Si hay solo dos, hay dos posibilidades:
- Las dos casillas están en la misma fila o columna: en ese caso tenemos una pareja puntero. También es información adicional, y podemos repetir el proceso con el mismo número.
- Las dos casillas están en filas y columnas diferentes: no es una pareja puntero, así que solo marcaremos esas casillas a lápiz.
Si hay tres casillas también hay dos posibilidades:
- Las tres están en la misma fila o columna: tenemos un trio puntero. Es información adicional, y podemos repetir el proceso con el mismo número.
- No están alineadas. En ese caso ignoramos esta situación.

Almacenaremos los valores encontrados en estructuras adecuadas de modo que puedan ser consultadas más adelante.

En lugar de crear un nuevo tablero, para almacenar la información de si en una casilla es posible colocar un valor, añadiremos un campo booleano a cada casilla, de este modo las clases de fila, columna y caja tendrán acceso a ese campo y nos facilitarán la tarea.

Añadiremos algunos datos y métodos a la clase casilla:

class Casilla {
    private:
    int fila,columna,caja,pos;
    int valor;
    bool posible;
    bool inicial;
    bool lapiz[9];

    public:
    Casilla(int f, int c, int v, bool ini);
    int Valor() const { return valor; }
    void Asignar(int v);
    int Fila() const { return fila; }
    int Columna() const { return columna; }
    int Caja() const { return caja; }
    int PosEnCaja() const { return pos; }
    bool Posible() const { return posible; }
    void MarcaPosible( bool p=true ) { posible = p; }
    void MarcaNoPosible() { posible = false; }
    void MarcaLapiz(int v) { lapiz[v-1] = true; }
    bool DesmarcaLapiz(int v);
    bool Lapiz(int v) { return lapiz[v-1]; }
    bool TieneMarcasLapiz() const;
    int NumeroMarcasLapiz() const;
    void Mostrar();
};

Los datos fila, columna, caja y pos se usan en algunos métodos para obtener la posición de una casilla.

posible se usará por nuestro algoritmo de cribado. Indicará si el valor que estamos verificando es posible en esta casilla. Para ello se añaden los métodos Posible, MarcaPosible y MarcaNoPosible.

El dato inicial también se usa internamente. Indica que el valor de la casilla corresponde a una de las pistas iniciales, y solo es útil a la hora de visualizar el tablero, para distinguir los valores iniciales de los que se van añadiendo. (En técnicas de resolución avanzada puede ser útil saber si el valor de una casilla es un valor inicial o no, pero de momento esto no es importante).

El array lapiz se usará para las "marcas a lápiz". Asignar un valor final a una casilla debe eliminar las marcas a lápiz.

Para cada clase: Fila, Columna y Caja añadiremos un método Criba. El código es el mismo para las tres clases:

void Fila::Criba() {
    for(int i=0; i<9; i++) cas[i]->MarcaNoPosible();
}

Para la clase Tablero añadiremos dos métodos: LimpiaCriba, que iniciará todas las casillas como posibles, antes de iniciar el proceso de cribado, y Criba que llevará a cabo el proceso de cribado de un valor concreto:

void Tablero::LimpiaCriba() {
    for(int f=0; f<9; f++) {
        for(int c=0; c<9; c++) {
            casilla[f][c].MarcaPosible();
        }
    }
}

void Tablero::Criba(int v) {
    LimpiaCriba();
    for(int i=0; i<9; i++) {
        if(fila[i].Presente(v)) fila[i].Criba();
        if(columna[i].Presente(v)) columna[i].Criba();
        if(caja[i].Presente(v)) caja[i].Criba();
    }
}

Completaremos este método más tarde para procesar las parejas y trios puntero.

Una vez realizada la criba tenemos que encontrar cajas con tres o menos casillas posibles. De momento nos limitaremos a procesar cajas, veremos más tarde si vale la pena hacerlo también con filas y columnas.

Añadiremos algunos métodos a la clase Caja.

Un método que cuente el número de casillas posibles:

int Caja::CuentaPosibles() {
    int cuenta=0;
    for(int i=0; i<9; i++)
        if(cas[i]->Posible()) cuenta++;
    return cuenta;
}

Tres métodos para obtener el valor de la primera, segunda y tercera casilla posible:

int Caja::PrimeroPosible() {
    for(int i=0; i<9; i++)
        if(cas[i]->Posible()) return i;
    return -1;
}

int Caja::SegundoPosible(int p) {
    for(int i=p+1; i<9; i++)
        if(cas[i]->Posible()) return i;
    return -1;
}

int Caja::TerceroPosible(int s) {
    for(int i=s+1; i<9; i++)
        if(cas[i]->Posible()) return i;
    return -1;
}

Para cada caja añadiremos dos array para almacenar las parejas/trios punteros, y los métodos correspondientes para asignar y leer sus valores:

class Caja {
    private:
    Casilla *cas[9];
    bool punteroFila[3][9];
    bool punteroColumna[3][9];
...
    void AsignaPunteroFila(int f, int v) { punteroFila[f][v-1] = true; }
    void AsignaPunteroColumna(int c, int v) { punteroColumna[c][v-1] = true; }
    bool PunteroFila(int f, int v) const { return punteroFila[f][v-1]; }
    bool PunteroColumna(int c, int v) const { return punteroColumna[c][v-1]; }
};

También actualizaremos estos array a medida que se vayan localizando parejas y trios punteros. Y por supuesto, modificaremos el procedimiento de criba para tener en cuenta estos punteros.

void Tablero::Criba(int v) {
    int ncaja=0;

    LimpiaCriba();
    // Aplicar criba a valores finales:
    for(int i=0; i<9; i++) {
        if(fila[i].Presente(v)) fila[i].Criba();
        if(columna[i].Presente(v)) columna[i].Criba();
        if(caja[i].Presente(v)) caja[i].Criba();
    }
    // Eliminar de la criba resto de casillas con valor final
    for(int f=0; f<9; f++) {
        for(int c=0; c<9; c++) {
            if(casilla[f][c].Valor()) casilla[f][c].MarcaPosible(false);
        }
    }
    // Aplicar criba a parejas y trios punteros de cajas:
    // No desmarcar como posibles las casillas miembros de parejas y trios punteros:
    for(int f=0; f<3; f++) { // Fila de cajas
        for(int c=0; c<3; c++) { // Columna de cajas
            for(int i=0; i<3; i++) { // Fila de punteros
                if(caja[ncaja].PunteroFila(i, v)) fila[f*3+i].CribaMenosCaja(c);
            }
            for(int i=0; i<3; i++) { // Columna de punteros
                if(caja[ncaja].PunteroColumna(i, v)) columna[c*3+i].CribaMenosCaja(f);
            }
            ncaja++;
        }
    }
}

// Procesar criba por cajas
bool Tablero::ProcesarCriba(int v) {
    bool retval = false;
    int p, s, t;
    int f, c;

    for(int i=0; i<9; i++) { // Verificar cada caja
        switch(caja[i].CuentaPosibles()) {
        case 1:
            // Final:
            p = caja[i].PrimeroPosible();
            f = caja[i].Cas(p)->Fila();
            c = caja[i].Cas(p)->Columna();
            casilla[f][c].Asignar(v);
            retval=true;
            break;
        case 2:
            // pareja puntero:
            p = caja[i].PrimeroPosible();
            s = caja[i].SegundoPosible(p);
            // Marcar en tablero
            caja[i].Cas(p)->MarcaLapiz(v);
            caja[i].Cas(s)->MarcaLapiz(v);
            // Verificar si p y s están alineados y guardar pareja puntero si lo están
            if(caja[i].Cas(p)->Fila() == caja[i].Cas(s)->Fila()) {
                if(caja[i].AsignaPunteroFila(caja[i].Cas(p)->Fila()%3, v, 2)) {
                    retval=true;
                }
            }
            if(caja[i].Cas(p)->Columna() == caja[i].Cas(s)->Columna()) {
                if(caja[i].AsignaPunteroColumna(caja[i].Cas(p)->Columna()%3, v, 2)) {
                    retval=true;
                }
            }
            break;
        case 3:
            // trio puntero:
            p = caja[i].PrimeroPosible();
            s = caja[i].SegundoPosible(p);
            t = caja[i].TerceroPosible(s);
            // Verificar si p, s y t están alineados y guardar trie puntero si lo están
            if(caja[i].Cas(p)->Fila() == caja[i].Cas(s)->Fila() && caja[i].Cas(p)->Fila() == caja[i].Cas(t)->Fila()) {
                if(caja[i].AsignaPunteroFila(caja[i].Cas(p)->Fila()%3, v, 3)) {
                    retval=true;
                }
            }
            if(caja[i].Cas(p)->Columna() == caja[i].Cas(s)->Columna() && caja[i].Cas(p)->Columna() == caja[i].Cas(t)->Columna()) {
                if(caja[i].AsignaPunteroColumna(caja[i].Cas(p)->Columna()%3, v, 3)) {
                    retval=true;
                }
            }
            break;
        }
    }
    return retval;
}

Algunos métodos, como el anterior, tienen un valor de retorno booleano. Esto nos servirá para saber si un procedimiento ha aportado información nueva, en cuyo caso podemos repetir el proceso. Si un grupo de procedimiento no aportan información en una iteración de un bucle, deberemos usar métodos más complejos que lo hagan.

Hemos tenido en cuenta que convertir un trio puntero en un par puntero también aporta información nueva.

Solo nos queda modificar el procedimiento de asignación para eliminar las marcas de lápiz. Recordemos que nuestras marcas de lápiz van por parejas en cada caja, de modo que al eliminar una de ellas, la otra marca es un valor final que deberemos asignar.

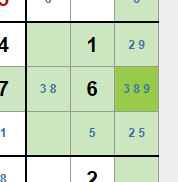
Esto que en principio parece fácil, puede tener algunas complicaciones. Por ejemplo en la caja de la derecha colocamos un 3 en la casilla marcada. Eso desencadena las siguientes asignaciones:

En la cuarta casilla, que contiene marcas a lápiz de 3 y 8, debemos colocar un 8.
En la tercera casilla, que contiene marcas a lápiz de 2 y 9, deberemos colocar un 9.
En la novena casilla, que contiene marcas a lápiz de 2 y 5, deberemos colocar un 2.
En la octava casilla, que contiene la única marca a lápiz de 5, colocaremos un 5.

¿Cómo programamos esto?

Podríamos complicar el algoritmo:

Asignamos el valor a la casilla, pero todavía no eliminamos las marcas a lápiz.
Eliminaremos las marcas a lápiz del valor asignado de todas casillas de la caja.
Para cada marca a lápiz de la casilla asignada, buscamos la casilla con la misma marca y repetimos el proceso recursivamente.

Pero no será necesario, ya que asignar un valor a una casilla aporta información, en la siguiente iteración podremos asignar el 8 a la cuarta casilla, y el 9 en la tercera, ya que serán la únicas posiciones posibles. En la siguiente iteración podremos asignar el 2 a la novena casilla y el 5 a la octava.

Bucle de resolución

En nuestra función main inicializaremos el tablero, verificaremos si tiene una única solución, y ejecutaremos un bucle que aplique los métodos de resolución mientras aporten información.

Nuestro bucle aún es relativamente simple:

    bool repetir;
    bool insistir;
...
    do {
        repetir=false;
        for(int v=1; v<=9; v++) {
            do {
                T.Criba(v);
                insistir = T.ProcesarCriba(v);
                repetir |= insistir;
            } while(insistir);
        }
    } while(repetir);

Se trata de dos bucles anidados. El exterior aplica la criba a cada posible valor de las casillas, y se repite siempre que para alguno de los valores de 1 a 9 se haya obtenido información nueva.

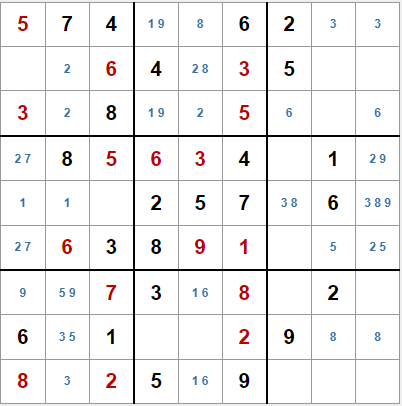
Con el programa en este punto, la solución parcial a la que llegamos con este sudoku en particular es la de la izquierda.

No está mal, pero aún estamos lejos de la solución final.

Salida del programa

Nos interesa que nuestro programa indique al usuario qué pasos seguir para resolver el sudoku.

Por una parte podemos mostrar en pantalla el estado del tablero después de aplicar cada método. Pero, salvo que paremos el programa en cada paso, el proceso es tan rápido que difícilmente se podrá seguir el proceso. Nuestros ejemplos realizan esta tarea, en parte como verificación de funcionamiento.

Pero la salida más interesante puede ser un fichero de texto con instrucciones detalladas, del tipo:

Par puntero fila F, valor 1
Par puntero fila E, valor 1
Par puntero columna 9, valor 2
Valor final 3 en D5
Par puntero columna 6, valor 3
Par puntero fila E, valor 3
Trio puntero columna 7, valor 4
Trio puntero columna 5, valor 4
Valor final 5 en C6
...

Pero en nuestro programa nos referiremos a nuestras filas y columnas con números entre 0 y 8, así que por claridad, en las salidas de texto nombraremos las filas con las letras 'A' a 'I', y las columnas con los números '1' a '9'.

Podríamos añadir líneas cuando se asignen o eliminen marcas de lápiz, pero probablemente sea contraproducente, así que en esta fase de la resolución no lo haremos.

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Sudoku2	sudoku2.zip	2022-06-22	4378 bytes	474