Resolución de sudokus (13)
Rectángulos vacíos
Rectángulos vacíos
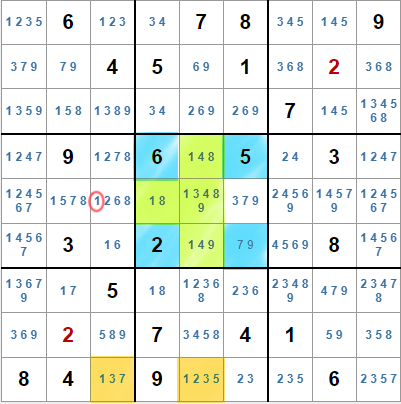
Esta técnica consiste en encontrar una caja k, en las que un candidato solo aparezca en una fila y una columna. A continuación hay que localizar una fila en la que el candidato solo aparezca en dos casillas, un una de esas casillas coincida con la columna de candidatos de la caja k. En la casilla que esté en la intersección de la columna de la otra casilla y en la fila de la caja k se podrá eliminar el valor como candidato.
El mismo razonamiento se puede aplicar partiendo de la fila de k.
Pero seguro que esto se entiende mejor con un ejemplo. En el sudoku de la derecha vemos que en la quinta caja el candidato 1 solo aparece en la fila E y la columna 5. En la fila I tenemos una pareja de casillas: I3 e I5 con el candidato 1, y la casilla I5 está en la misma columna que los candidatos de la caja de la que partimos. Si consideramos que en la caja 5, el valor 1 está en una de las casillas de la columna 5 (D5, E5 o F5), no podrá estar en I5, por lo tanto, deberá estar en I3. Eso elimina el candidato 1 de E3. Si por el contrario, consideramos que el ja caja 5, el valor 1 está en una de las casillas de la fila E, también se elimina el candidato 1 de E3.
Es decir, en cualquier caso, independientemente de la casilla en que finalmente esté el valor 1 en la caja 5, no podrá estar en E3.
Para este método no importa cuantas casillas de cada fila o columna de la caja tengan el candidato, siempre que solo aparezcan en una fila y en una columna. Por ejemplo, las caja 3, 6, 7 y 8 también tienen el patrón para el valor 1, aunque no permiten eliminar candidatos. Incluso, aunque el candidato solo aparezca en dos casillas de la misma fila o columna de una caja, es un patrón válido para dos rectángulos vacíos.
Esta técnica recibe este nombre porque, si eliminamos una fila y columna de una caja nos quedan cuatro casillas formando un rectángulo (aunque sea un cuadrado). En nuestro ejemplo el rectángulo vacío lo forman las casillas marcadas en azul.
Nuestra primera tarea es buscar patrones de rectángulos vacíos. No es una tarea sencilla.
Existen nueve posibles patrones, las 'X' indican casillas sin el candidato, el resto pueden tenerlo o no:
i= 0 1 2 3 4 5 6 7 8 +-- -+- --+ -XX X-X XX- -XX X-X XX- -XX X-X XX- +-- -+- -+- -XX X-X XX- -XX X-X XX- -XX X-X XX- +-- -+- --+ 033 055 066 303 505 606 330 550 660
Como de costumbre, convertiremos los patrones a mapas de bits, un 1 indica una casilla vacía (sin el candidato) y un 0 una casilla llena (con el candidato). Los números debajo de cada patrón indican los valores de bits que deben aparecer.
En nuestro ejemplo, si calculamos los tres valores para las tres filas de la caja, obtenemos: 5, 1 y 5, y si aplicamos AND de bits con cada uno de los patrones, con el único que queda intacto es el quinto:
5 & 5 = 5 0 & 1 = 0 5 & 5 = 5
Si probamos, por ejemplo, con el primero:
5 & 0 = 0 1 & 3 = 1 5 & 3 = 1
El orden de los patrones no se ha elegido de cualquier manera. Si calculamos el módulo del índice entre 3 obtendremos el valor de la columna con los candidatos. Si calculamos al división entera del índice entre 3, obtendremos el valor de la fila con los candidatos.
En nuesto ejemplo, el valor del índice del patrón que coincide es 4. 4%3=1, 4/3=1, es decir, la segunda fila y segunda columna de la caja.
Añadiremos un método a la clase caja para calcular el patrón de rectángulo vacío para un valor concreto:
class Caja {
private:
...
public:
...
int RectanguloVacio(int v);
};
Y lo implementaremos:
int Caja::RectanguloVacio(int v) {
int ff[3] = {0, 0, 0};
int trama[9][3] = {0,3,3, 0,5,5, 0,6,6, 3,0,3, 5,0,5, 6,0,6, 3,3,0, 5,5,0, 6,6,0};
int retval = -1;
if(!Presente(v)) {
for(int p=0; p<9; p++) {
if(!cas[p]->Lapiz().ContieneMarca(v)) {
ff[cas[p]->Fila()%3] |= (4 %gt;> (p%3));
}
}
for(int t=0; t<9; t++) {
if((trama[t][0] == (ff[0] & trama[t][0])) &&
(trama[t][1] == (ff[1] & trama[t][1])) &&
(trama[t][2] == (ff[2] & trama[t][2]))) {
retval = t;
}
}
}
return coincidencia;
}
Con esto ya tenemos buena parte del procedimiento. Ahora añadiremos un método a la clase Tablero para procesar rectángulos vacíos.
class Tablero {
private:
...
public:
...
void ResaltarCandidato(int v);
...
};
Y la implementación:
bool Tablero::ProcesaRectangulosVacios() {
int rv;
int f, c;
int f2, c2;
Pareja par;
for(int v=1; v<=9; v++) {
// En cada caja buscar patrones de rectángulos vacíos
for(int k=0; k<9; k++) {
rv = caja[k].RectanguloVacio(v);
if(-1 != rv) {
f = 3*(k/3) + rv/3;
c = 3*(k%3) + rv%3;
// Buscar par puntero en columnas con un candidato en fila f
for(int c1=0; c1<9; c1++) {
par = columna[c1].DobleCandidato(v);
if(par.Cas(0) && // Si encuentra un par
!par.MismaCaja() && // El par no está en la misma caja
// Y está en una fila de cajas distinta a la del rectángulo
(par.Cas(0)->Caja() != k) && (par.Cas(1)->Caja() != k) &&
// Y una de las casillas coincide con la fila en el rectángulo
(par.Cas(0)->Fila() == f || par.Cas(1)->Fila() == f)) {
if(par.Cas(0)->Fila() == f) f2 = par.Cas(1)->Fila();
else f2 = par.Cas(0)->Fila();
if(casilla[f2][c].Lapiz().EliminarMarca(v)) {
return true;
}
}
}
// Buscar par puntero en filas con un candiadto en fila c
for(int f1=0; f1<9; f1++) {
par = fila[f1].DobleCandidato(v);
if(par.Cas(0) &&
!par.MismaCaja() &&
(par.Cas(0)->Caja() != k) && (par.Cas(1)->Caja() != k) &&
(par.Cas(0)->Columna() == c || par.Cas(1)->Columna() == c)) {
if(par.Cas(0)->Columna() == c) c2 = par.Cas(1)->Columna();
else c2 = par.Cas(0)->Columna();
if(casilla[f][c2].Lapiz().EliminaMarca(v)) {
return true;
}
}
}
}
}
}
return false;
}
Una vez que tenemos un patron de rectángulo vacío para una caja y candidato, buscaremos una fila con el mismo candidato en dos casillas.
Esta pareja debe cumplir varias condiciones:
- Las dos casillas no pueden estar en la misma caja.
- La fila no debe estar en la misma fila de cajas que la caja que contiene el patrón.
- Una de las casillas debe estar en la columna del patrón.
Si se cumplen todas las condiciones, podemos eliminar el candidato en la casilla en la columna del patrón y la fila de la otra casilla de la pareja.
Podemos repetir el mismo proceso con la columna.
Bucle de resolución
Finalmente, completamos el bucle de resolución:
if(!repetir && T.ProcesaRectangulosVacios()) {
repetir = true;
T.VerificarFinales();
}
Medusa
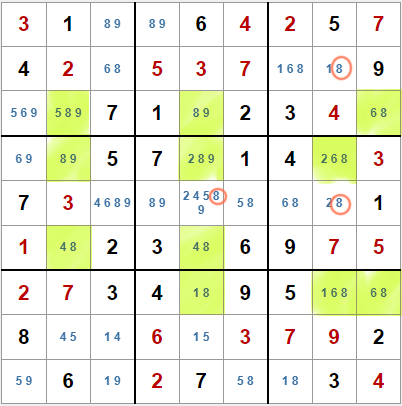
El patrón medusa o jellyfish es una extensión del X-Wing y el pez espada. Así como en X-Wing se buscan dos filas o columnas para un candidato, y en el pez espada tres, en la estructura medusa se trata de buscar cuatro filas o columnas en las que un candidato aparezca en solo cuatro columnas o filas, respectivamente.
El algoritmo es el mismo que para el pez espada, pero añadiendo otro nivel.
Empezaremos por añadir algunas funciones a nuestra clase Tablero:
class Tablero {
private:
...
bool BuscaJellyFishFilas(int v);
bool BuscaJellyFishColumnas(int v);
bool ProcesaJellyFishFilas(MarcasCasillas, MarcasCasillas, int v);
bool ProcesaJellyFishColumnas(MarcasCasillas, MarcasCasillas, int v);
public:
...
bool ProcesaJellyFish();
...
};
Para buscar el patrón de medusa en filas:
bool Tablero::BuscaJellyFishFilas(int v) {
bool retval=false;
MarcasCasillas CasillasFilas;
MarcasCasillas CasillasColumnas;
for(int f1=0; f1<6; f1++) {
// Buscamos en las primeras 6 filas en las que no aparezca v
// y esté como candidato en 2, 3 o 4 columnas:
if(!fila[f1].Presente(v) && fila[f1].CuentaCandidato(v) <= 4) {
// Ahora buscamos las filas f1+1 a septima otra que tenga 2, 3 o 4 candidatos v.
for(int f2= f1+1; f2<7; f2++) {
if(!fila[f2].Presente(v) && fila[f2].CuentaCandidato(v) <= 4) {
// Si entre las dos filas, el candidato aparece en 3 o 4 columnas, buscamos otra fila
CasillasColumnas = fila[f1].Marcas(v)+fila[f2].Marcas(v);
if(CasillasColumnas.CuentaCasillas() <= 4) {
// Ahora buscamos las filas f2+1 a octava otra que tenga 2, 3 o 4 candidatos v en las
// mismas columnas que las anteriores.
for(int f3=f2+1; f3<8; f3++) {
if(!fila[f3].Presente(v) && fila[f3].CuentaCandidato(v) <= 4) {
CasillasColumnas = fila[f1].Marcas(v)+fila[f2].Marcas(v)+fila[f3].Marcas(v);
if(CasillasColumnas.CuentaCasillas() <= 4) {
// Ahora buscamos las filas f3+1 a novena otra que tenga 2, 3 o 4 candidatos v en las
// mismas columnas que las anteriores.
for(int f4=f3+1; f4<9; f4++) {
if(!fila[f4].Presente(v) && fila[f4].CuentaCandidato(v) <= 4) {
CasillasColumnas = fila[f1].Marcas(v)+fila[f2].Marcas(v)+fila[f3].Marcas(v)+fila[f4].Marcas(v);
if(CasillasColumnas.CuentaCasillas() == 4) {
// Tenemos una medusa.
CasillasFilas.AsignaCasilla(f1);
CasillasFilas.AsignaCasilla(f2);
CasillasFilas.AsignaCasilla(f3);
CasillasFilas.AsignaCasilla(f4);
if(ProcesaJellyFishFilas(CasillasFilas, CasillasColumnas, v)) return true;
}
}
}
}
}
}
}
}
}
}
}
return retval;
}
La función para buscar en columnas es similar.
Para procesar el patrón detectado usaremos una función muy parecida a la del patrón pez espada:
bool Tablero::ProcesaJellyFishFilas(MarcasCasillas fils, MarcasCasillas cols, int v) {
bool retval = false;
for(int f=0; f<9; f++) {
if(!fils.ContieneCasilla(f)) {
for(int c=0; c<9; c++) {
if(cols.ContieneCasilla(c)) {
retval |= casilla[f][c].Lapiz().EliminaMarca(v);
}
}
}
}
return retval;
}
Y la de columnas es equivalente.
Por último, añadimos las líneas correspondientes al bucle de resolución.
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku17 | sudoku17.zip | 2022-06-22 | 34411 bytes | 648 |