Resolución de sudokus (12)
Sashimi y rascacielos
Sashimi X-Wing
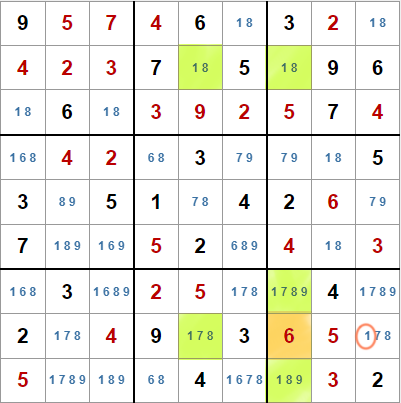
Para comprender esta técnica hay que verla como un X-Wing con alas en el que falta el candidato en la casilla que tiene el o las alas.
Veamos el ejemplo de la derecha. Si en la casilla marcada en naranja, en lugar de un valor final estuviera vacía, también podríamos colocar la marca de lápiz para el valor 1. Por lo tanto, el razonamiento para eliminar casillas que hicimos para el X-Wing con alas es válido para este patrón también.
La explicación es la misma. Si colocamos un uno en cualquiera de las dos casillas G7 o I7, podemos eliminar como candidato el 1 en H9 , B7 y H5. Si por el contrario, el valor 1 no está ni en G7 ni en H7, deberá estar en B7, lo que implica que no puede estar en B5, así que debe estar en H5, lo que elimina el candidato 1 de H9.
En cualquiera de los dos supuestos, el candidato de H9 siempre es eliminado. También podríamos eliminarlo de H8 si estuviese.
Para este patrón es necesario que las dos casillas que completan el patrón en la caja donde está el valor final tengan el candidato. Si solo lo tiene una de ellas el razonamiento sigue siendo válido, pero como veremos en el siguiente método, a menudo se podrán eliminar candidatos de otras casillas.
A estas alturas ya habrás notado que es frecuente usar nombres de peces para algunos métodos. El sashimi es una forma de preparar el pescado en la cocina japonesa, y en los sudokus se usa para indicar que se ha presentado un pescado de una forma concreta (crudo y en lonchas). Así como en la cocina existen sashimis de varios tipos de pescado, en los sudokus también hay varios tipos de sashimis. Se puede aplicar a X-Wing, como este caso, pero también a Swordfish (pez espada) y a Jellyfish (medusa). Tal vez veamos estos métodos en otros capítulos. Y sí, a mi también me suena raro el sashimi de X-Wing.
Dividiremos la tarea en filas y columnas.
Para las filas, nuestro algoritmo buscará, para cada posible valor, una fila con el candidato en dos columnas. Ya disponemos de las funciones necesarias para buscar estas coincidencias.
Una vez localizada una pareja de casillas buscaremos en el resto de filas una en la que el valor esté como candidato en una de las columnas de la fila anterior, y en la otra columna haya un valor asignado. Solo nos queda asegurarnos de que en esta segunda fila el candidato solo aparezca en la caja de esa segunda fila y columna, las casillas del resto de la columna tengan la marca de lápiz del candidato. Además, en esa columna el candidato debe aparecer tres veces.
Será útil añadir una función a nuestra clase Pareja, para verificar si las dos casillas pertenecen a la misma caja:
class Pareja {
...
public:
...
bool MismaCaja() { return cas[0]->Caja() == cas[1]->Caja(); }
};
Añadiremos algunas funciones a la clase Tablero:
class Tablero {
private:
...
bool BuscaSashimiFilas();
bool BuscaSashimiColumnas();
bool ProcesarSashimiFila(int f, int c, int v);
bool ProcesarSashimiColumna(int f, int c, int v);
public:
...
bool ProcesaSashimi();
...
};
Para buscar patrones sashimi por filas:
bool Tablero::BuscaSashimiFilas() {
Pareja par;
int c, c1, c2;
int k, cuenta;
for(int v=1; v<=9; v++) {
for(int f1=0; f1<8; f1++) {
par = fila[f1].DobleCandidato(v);
if(par.Cas(0) && !par.MismaCaja() ) {
c1 = par.Cas(0)->Columna();
c2 = par.Cas(1)->Columna();
for(int f2=0; f2<9; f2++) {
if(f2 != f1) {
c = -1;
if(casilla[f2][c1].Lapiz().ContieneMarca(v) && casilla[f2][c2].Valor()) c = c2;
if(casilla[f2][c2].Lapiz().ContieneMarca(v) && casilla[f2][c1].Valor()) c = c1;
if(c != -1) {
k = casilla[f2][c].Caja();
// Contar casillas con candidato v en fila f2 y caja k
cuenta=0;
for(int p=0; p<9; p++) {
if(caja[k].Cas(p)->Columna() == c && caja[k].Cas(p)->Lapiz().ContieneMarca(v)) cuenta++;
}
if(cuenta==2 && columna[c].CuentaCandidato(v) == 3) {
// Posible, depende de si hay candidatos a eliminar:
if(ProcesarSashimiFila(f1, f2, c1, c2, v, c)) return true;
}
}
}
}
}
}
}
return false;
}
La función para columnas es similar.
Procesar los patrones localizados es más simple:
bool Tablero::ProcesarSashimiFila(int f, int c, int v) {
int retval = false;
int k = casilla[f][c].Caja();
for(int p=0; p<9; p++) {
if(caja[k].Cas(p)->Fila() == f && caja[k].Cas(p)->Columna() != c)
retval |= caja[k].Cas(p)->Lapiz().ContieneMarca(v);
}
return retval;
}
Finalmente, ProcesarSashimi sencillamente llama a las dos funciones de búsqueda:
bool Tablero::ProcesaSashimi() {
if(BuscaSashimiFilas()) return true;
if(BuscaSashimiColumnas()) return true;
return false;
}
Bucle de resolución
Por supuesto, como siempre:
do {
...
if(!repetir && T.ProcesaSashimi()) {
repetir = true;
T.VerificarFinales();
}
} while(repetir);
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku15 | sudoku15.zip | 2022-06-22 | 19737 bytes | 691 |
Rascacielos
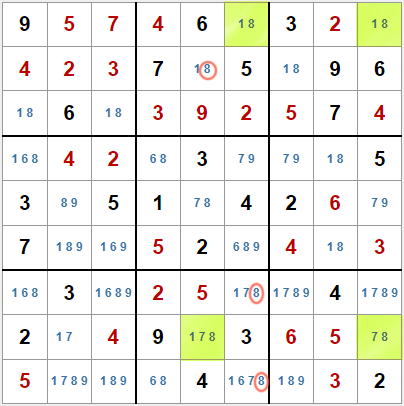
El rascacielos, o skyscraper, es una variante del sashimi X-Wing. En el ejemplo de la izquierda vemos que el candidato 8 aparece solo en dos casillas de las filas A y H, coincidiendo en la columna 9 y en la segunda columna de cajas, en las columnas 5 y 6. Podemos ver éste patrón como dos sashimis superpuestos, eliminando el candidato 8 de las casillas de la columna 5 de la segunda caja y de las casillas de la columna 6 en la octava caja.
Pero el algoritmo para buscar sashimis, aunque se modificara, no es fácil de adaptar para buscar dos patrones simultáneamente, así que buscaremos este patrón concreto y lo trataremos a parte.
Localizar estas estructuras es algo más sencillo que hacerlo con sashimis.
Para filas, para cada posible valor primero buscaremos una con dos candidatos que no estén en la misma caja. Si la encontramos, buscaremos en el resto de filas otra con dos candidatos para el mismo valor, que cumplan las siguientes condiciones:
- Que cada una de las casillas de cada pareja esté en la misma columna de cajas.
- Que las dos filas no estén en la misma línea de cajas.
- Que solo una de las casillas de cada línea estén en la misma columna.
En ese caso, procesaremos el patrón para verificar si se puede eliminar algún candidato.
Añadiremos algunos métodos más a nuestra clase Tablero:
class Tablero {
private:
...
bool BuscaSkyscraperFilas();
bool BuscaSkyscraperColumnas();
bool ProcesarSkyscraperFila(Pareja &par1, Pareja &par2, int np, int v);
bool ProcesarSkyscraperColumna(Pareja &par1, Pareja &par2, int np, int v);
public:
...
bool ProcesaSkyscraper();
...
};
Para buscar patrones en filas:
bool Tablero::BuscaSkyscraperFilas() {
Pareja par1, par2;
for(int v=1; v<=9; v++) {
for(int f1=0; f1<8; f1++) {
par1 = fila[f1].DobleCandidato(v);
// La pareja de candidatos no puede estar en la misma caja
if(par1.Cas(0) && par1.Cas(0)->Caja() != par1.Cas(1)->Caja()) {
for(int f2=f1+1; f2<9; f2++) {
par2 = fila[f2].DobleCandidato(v);
if(par2.Cas(0)) {
// Las casillas de cada pareja deben estar en las misma columna de cajas, y en distintas cajas
if(par1.Cas(0)->Caja()%3 == par2.Cas(0)->Caja()%3 &&
par1.Cas(1)->Caja()%3 == par2.Cas(1)->Caja()%3 &&
par1.Cas(0)->Caja() != par2.Cas(0)->Caja()){
// Segunda condición:
// Una de las casillas de cada pareja debe estar en la misma columna
if(par1.Cas(0)->Columna() == par2.Cas(0)->Columna() &&
par1.Cas(1)->Columna() != par2.Cas(1)->Columna()) {
if(ProcesarSkyscraperFila(par1, par2, 1, v)) return true;
}
if(par1.Cas(0)->Columna() != par2.Cas(0)->Columna() &&
par1.Cas(1)->Columna() == par2.Cas(1)->Columna()) {
if(ProcesarSkyscraperFila(par1, par2, 0, v)) return true;
}
}
}
}
}
}
}
return false;
}
Procesar los patrones es fácil:
bool Tablero::ProcesarSkyscraperFila(Pareja &par1, Pareja &par2, int np, int v) {
bool retval = false;
int k1, k2;
k1 = par1.Cas(np)->Caja();
k2 = par2.Cas(np)->Caja();
for(int f=0; f<9; f++) {
if(casilla[f][par1.Cas(np)->Columna()].Caja() == k2) {
retval |= casilla[f][par1.Cas(np)->Columna()].Lapiz().EliminaMarca(v);
}
if(casilla[f][par2.Cas(np)->Columna()].Caja() == k1) {
retval |= casilla[f][par2.Cas(np)->Columna()].Lapiz().EliminaMarca(v);
}
}
return retval;
}
Procesar el tablero buscando patrones rascacielos también es sencillo:
bool Tablero::ProcesaSkyscraper() {
if(BuscaSkyscraperFilas()) return true;
if(BuscaSkyscraperColumnas()) return true;
return false;
}
Bucle de resolución
Solo queda añadir la llamada en el bucle de resolución:
do {
...
if(!repetir && T.ProcesaSkyscraper()) {
repetir = true;
T.VerificarFinales();
}
} while(repetir);
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku16 | sudoku16.zip | 2022-06-22 | 32460 bytes | 663 |