Resolución de sudokus (10)

Patrones de solución única.

Casillas con dos candidatos menos una

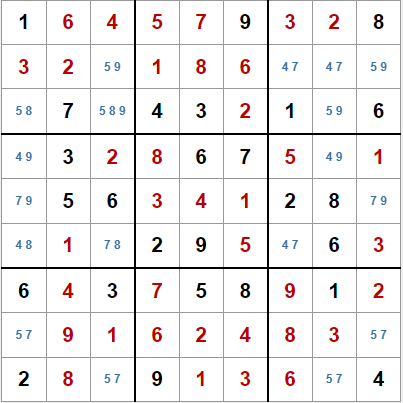
Volvamos a este sudoku que nos quedó al aplicar el patrón X-Wing. Este tablero tiene una característica muy interesante: todas las casillas vacías tienen dos candidatos, excepto una que tiene tres.

Nos faltan por colocar casillas con valores 4, 5, 7, 8 y 9. Pero si nos fijamos en cada uno de esos valores, el candidato aparece en dos casillas de cada fila, columna y caja. Eso significa que para cada candidato existen dos posibles soluciones, si podemos fijar el valor de un candidato en una casilla, fijaremos el valor de ese candidato en el resto, pero si lo hacemos para la casilla emparejada en la misma fila, columna o caja, también. Esto es cierto para todos los valores, excepto el 5.

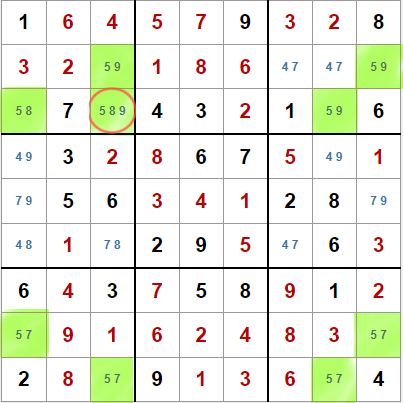
Pongamos nuestra atención en el 5. En la primera caja es en la única en que aparece en tres casillas. ¿Qué pasaría si el 5 NO estuviera en la casilla marcada, de la tercera fila y tercera columna?

En ese caso, también habría dos posibles soluciones para el sudoku para el valor 5, y por lo tanto, (potencialmente) para el sudoku completo. Sin embargo, sabemos que el sudoku solo puede tener una solución, así que obligatoriamente, en la casilla de la tercera fila y tercera columna ha de haber un 5.

El mismo razonamiento sirve si consideramos la tercera fila o la tercera columna, en la que el 5 aparece como candidato en tres casillas.

Evidentemente, si el sudoku es válido y eliminamos el candidato 5 en esa posición descubriremos que no podemos llegar a una solución, ya que, en algún momento, alguna casilla se quedará sin candidatos. De hecho, si recordamos el capítulo de la técnica X-Wing con aletas, precisamente se eliminaba el candidato 5 de las otras dos casillas.

Ahora veamos cómo implementar el algoritmo que detecte y procese un patrón en que todas las casillas tienen dos candidatos menos una que tenga tres. Primero añadimos la declaración:

class Tablero {
...
    public:
...
    bool TodasConDosCandidatosMenosUna();
...
};

La implementación no es muy complicada. Miramos para cada casilla, si alguna tiene más de tres candidatos, retornamos false. Si más de una tiene tres candidatos, retornamos false. Hemos almacenado la última casilla con tres candidatos, así que si no hemos retornado, localizamos en esa casilla la marca de lápiz que aparezca tres veces en su fila (o columna o caja), y asignaremos ese valor a la casilla:

bool Tablero::TodasConDosCandidatosMenosUna() {
    int cuenta3Candidatos=0;
    Casilla *cas3;

    // Buscar en cada casilla, si el número de candidatos en más de una es tres
    // o en alguna hay más de tres, retornar false
    for(int f=0; f<9; f++) {
        for(int c=0; c<9; c++) {
            if(casilla[f][c].Lapiz().CuentaMarcas() > 3) return false;
            if(casilla[f][c].Lapiz().CuentaMarcas() == 3) { cas3 = &casilla[f][c]; cuenta3Candidatos++; }
            if(cuenta3Candidatos > 1) return false;
        }
    }
    if(cuenta3Candidatos == 0) return false; // En éste caso el sudoku estará resuelto
    // Si no hemos retornado false, tenemos un patrón en el que todas las casillas
    // con candidatos tienen dos, menos una que tiene 3.
    // La casilla (f3,c3) es la que tiene tres candidatos, en la fila f3, la columna c3 y
    // en la caja donde está esa casilla hay un candidato que aparece 3 veces, localizarlo.
    for(int v=1; v<=9; v++) {
        if(cas3->Lapiz().ContieneMarca(v) && fila[cas3->Fila()].CuentaCandidato(v) == 3) {
            // Marcar valor final v en cas3
            Asignar(cas3->Fila(), cas3->Columna(), v);
        }
    }
    return true;
}

Daremos prioridad a este procedimiento sobre otros como el X-Wing con alas o el Pez espada. Es decir, colocaremos la llamada a esta función antes de las de X-Wing o Pez espada.

Bucle de resolución

En nuestro bucle añadiremos éste código:

    do {
...
        if(!repetir && T.TodasConDosCandidatosMenosUna()) {
            repetir = true;
            T.VerificarFinales();
        }
...
    } while(repetir);

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Sudoku11	sudoku11.zip	2022-06-22	28466 bytes	435

Patrones de solución única

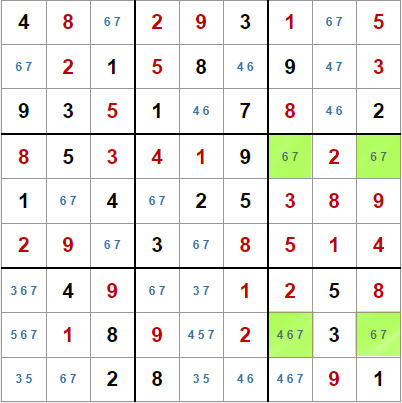
Veamos el ejemplo del sudoku de la derecha. Tres de las cuatro casillas resaltadas en verde contienen los candidatos 6 y 7, y la otra, además de esos valores, el valor 4.

Se trata de una situación parecida a la anterior, pero restringida a cuatro casillas formando un rectángulo, pero ocupando solo dos cajas. Podemos hacer el un razonamiento parecido.

Supongamos ahora que la casilla con tres candidatos no contuviera el valor 4. En ese caso, el sudoku tendría al menos dos soluciones. Pero sabemos, o al menos esperamos, que estamos resolviendo un sudoku válido que solo tiene una solución (en nuestro caso nos hemos asegurado desde el principio que es así), por lo tanto, en la casilla de la octava fila y séptima columna debe haber forzosamente un 4.

Podemos ampliar el patrón un poco más. En la casilla que contiene más de dos candidatos puede haber tres o más. La diferencia es que ahora no tendremos un valor final, simplemente podremos eliminar de esa casilla la pareja de candidatos que comparten las cuatro casillas del patrón.

Para localizar estos patrones usaremos la lista que ya tenemos de pares desnudos. Si un par desnudo está en una fila buscaremos otra fila, si está en una columna, buscaremos otra columna que complete el patrón, es decir, que contenga las mismas marcas de lápiz en las mismas columnas o filas, y en una de las casillas una marca de lápiz extra.

En la clase Tablero añadiremos tres métodos.

class Tablero {
    private:
...
    bool BuscaFila(Desnudo des);
    bool BuscaColumna(Desnudo des);
    public:
...
    bool SolucionUnicaA();
...
};

SolucionUnicaA procesará el tablero buscando potenciales patrones de solución única, a través de la lista de pares desnudos:

bool Tablero::SolucionUnicaA() {
    int ff, cc;

    LimpiaResaltes();
    desnudo.Primero();
    while(desnudo.Actual()) {
        // Si se trata de un par desnudo y las dos casillas están en la misma caja
        if(desnudo.ValorActual().Par() && desnudo.ValorActual().MismaCaja() != -1) {
            ff = desnudo.ValorActual().MismaFila();
            cc = desnudo.ValorActual().MismaColumna();
            if(-1 != ff) { // El par desnudo está en una fila
                // Buscar en filas
                if(BuscaFila(desnudo.ValorActual())) return true;
            }
            if(-1 != cc) {
                // Buscar en columnas
                if(BuscaColumna(desnudo.ValorActual())) return true;
            }
        }
        desnudo.Siguiente();
    }
    return false;
}

Y dos métodos auxiliares que buscarán casillas que completen los patrones potenciales detectados en filas o columnas. Ambos métodos son similares:

bool Tablero::BuscaFila(Desnudo des) {
    bool retval=false;
    int c1, c2, ff;
    int nMarcas1, nMarcas2;
    Casilla *cas3 = NULL;
    char cad[100];

    ff = des.Cas(0)->Fila();
    c1 = des.Cas(0)->Columna();
    c2 = des.Cas(1)->Columna();
    for(int f=0; f<9; f++) {
        if(f != ff) {
            nMarcas1 = casilla[f][c1].Lapiz().CuentaMarcas();
            nMarcas2 = casilla[f][c2].Lapiz().CuentaMarcas();

            if(nMarcas1==2 && nMarcas2>=3 &&
               casilla[f][c1].Lapiz() == des.Cas(0)->Lapiz() &&
               (casilla[f][c2].Lapiz() ^ des.Cas(0)->Lapiz()) == des.Cas(0)->Lapiz()) {
                cas3 = &casilla[f][c2];
            } else
            if(nMarcas1>=3 && nMarcas2==2 &&
               casilla[f][c2].Lapiz() == des.Cas(0)->Lapiz() &&
               (casilla[f][c1].Lapiz() ^ des.Cas(0)->Lapiz()) == des.Cas(0)->Lapiz()) {
                cas3 = &casilla[f][c1];
            } else
            if(nMarcas1>=3 && nMarcas2==2 &&
               casilla[f][c2].Lapiz() == des.Cas(0)->Lapiz() &&
               (casilla[f][c1].Lapiz() ^ des.Cas(0)->Lapiz()) == des.Cas(0)->Lapiz()) {
                cas3 = &casilla[f][c1];
            }
        }
    }
    if(cas3) {
        for(int v=1; v<=9; v++) {
            if(des.Cas(0)->Lapiz().ContieneMarca(v)) {
                cas3->Lapiz().EliminaMarca(v);
            }
        }
        return true;
    }
    return false;
}

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Sudoku12	sudoku12.zip	2022-06-22	29185 bytes	426

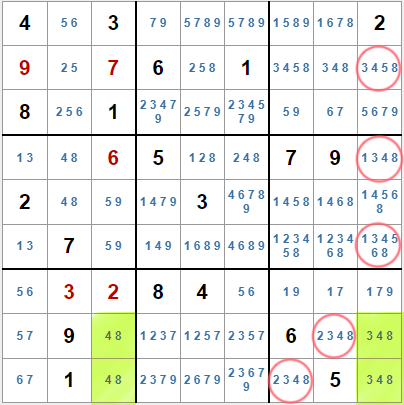
Hay más situaciones que podemos aprovechar para eliminar candidatos.

Supongamos que tenemos una situación como la del ejemplo de la derecha.

Ahora no podemos eliminar ningún candidato de las casillas con tres candidatos, pero sí podemos asegurar que el candidato extra estará en una de las dos casillas, por lo que se convierte en un par puntero, y podremos eliminarlo del resto de casillas de la fila, y si están en la misma caja, también del resto de casillas de esa caja.

De nuevo añadiremos tres métodos a la clase Tablero.

class Tablero {
    private:
...
    bool BuscaFilaTrios(Desnudo des);
    bool BuscaColumnaTrios(Desnudo des);
    public:
...
    bool SolucionUnicaB();
...
};

SolucionUnicaB procesará el tablero buscando potenciales patrones de solución única, a través de la lista de pares desnudos:

bool Tablero::SolucionUnicaB() {
    int ff, cc;

    desnudo.Primero();
    while(desnudo.Actual()) {
        ff = desnudo.ValorActual().MismaFila();
        cc = desnudo.ValorActual().MismaColumna();
        if(-1 != ff && desnudo.ValorActual().Par()) { // El par desnudo está en una fila
            // Buscar en filas
            if(BuscaFilaTrios(desnudo.ValorActual())) return true;
        }
        if(-1 != cc && desnudo.ValorActual().Par()) {
            if(BuscaColumnaTrios(desnudo.ValorActual())) return true;
        }
        desnudo.Siguiente();
    }
    return false;
}

Buscar el resto del patrón consiste en buscar dos casillas con tres candidatos iguales y que compartan candidatos con el par desnudo:

bool Tablero::BuscaFilaTrios(Desnudo des) {
    bool retval=false;
    int c1, c2, ff;
    MarcasLapiz m;
    int v;

    ff = des.Cas(0)->Fila();
    c1 = des.Cas(0)->Columna();
    c2 = des.Cas(1)->Columna();
    for(int f=0; f<9; f++) {
        if(f != ff) {
            if(casilla[f][c1].Lapiz().CuentaMarcas()==3 && casilla[f][c2].Lapiz().CuentaMarcas()==3 &&
               casilla[f][c1].Lapiz() == casilla[f][c2].Lapiz() &&
               (casilla[f][c1].Lapiz() ^ des.Cas(0)->Lapiz()) == (casilla[f][c2].Lapiz() ^ des.Cas(0)->Lapiz())) {
                m = casilla[f][c1].Lapiz() - des.Cas(0)->Lapiz(); // Marca extra
                v = m.Valor(); // Valor de la marca extra
                // Eliminar v del resto de la fila f
                for(int c=0; c<9; c++)
                    if(c != c1 && c!= c2) retval |= casilla[f][c].Lapiz().EliminaMarca(v);
                // Si el par desnudo está en la misma caja, también se puede eliminar v del resto de la caja del trio
                if(casilla[f][c1].Caja() == casilla[f][c2].Caja()) {
                    int k = casilla[f][c1].Caja();
                    for(int p=0; p<9; p++)
                        if(caja[k].Cas(p)->Fila() != f) retval |= caja[k].Cas(p)->Lapiz().EliminaMarca(v);
                }
            }
        }
    }
    return retval;
}

Y la función para columnas es parecida.

Bucle de resolución

Por supuesto, solo queda añadir este procedimiento al bucle de resolución.

    do {
...
        if(!repetir && T.SolucionUnicaB()) {
            repetir = true;
            T.VerificarFinales();
        }
    } while(repetir);

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Sudoku13	sudoku13.zip	2022-06-22	29713 bytes	415