Resolución de sudokus
Reglas y Sudokus válidos
El juego

El sudoku es un juego, o pasatiempo, que se ha hecho muy popular. A mucha gente, yo incluido, le resulta muy entretenido.
En principio podría considerarse que está en la misma categoría que los crucigramas y otros juegos que se suelen incluir en revistas de pasatiempos. Sin embargo, algunas de sus características, como que pueden ser generados automáticamente, y que sus reglas y el modo de resolverlos son simples, los hace muy adecuados para dispositivos como teléfonos móviles y ordenadores.
Según la Wikipedia:
El Sudoku es un juego matemático que se inventó a finales de la década de 1970, adquirió popularidad en Japón en la década de 1980, y se dio a conocer en el ámbito internacional en 2005, cuando numerosos periódicos empezaron a publicarlo en su sección de pasatiempos.
Ahora bien, a mi modo de ver, no se trata de un juego matemático. Aunque generalmente se usan números, pueden resolverse usando letras, dibujos o cualquier otro símbolo. Se trata más bien de un tipo de puzzle, donde el objetivo es encajar todas las piezas.
Reglas
En su forma más conocida consiste en una cuadrícula de 9x9 casillas. La cuadrícula se divide en 9 filas, 9 columnas y 9 cajas de 3x3 casillas. En cada casilla hay que colocar un número entre 1 y 9, de tal modo que en cada fila, columna y caja no se repita ningún número. Se suministran ciertos valores iniciales para algunas de casillas, de modo que el jugador pueda completar el resto.
Un sudoku válido solo puede tener una solución. Si fuera posible resolverlo de varias formas no se considera un sudoku válido.
El número mínimo de pistas es 17, y al menos debe haber pistas para 8 de los valores.
Y en lo que respecta a las reglas, eso es todo. Lo divertido es resolverlos.
Categorías
En las revistas, periódicos y aplicaciones móviles encontrarás que los sudokus se clasifican en varias categorías en función de su dificultad: fáciles, difíciles, para expertos, etc. En principio se trata de categorías arbitrarias. Depende de cómo se resuelvan los sudokus, lo que a algunos les parece difícil, a otros puede parecerles fácil.
Según mi criterio, la dificultad debería estar ligada al nivel de las técnicas necesarias para resolverlos. Y aunque pueda parecer lo contrario, un sudoku con más pistas no es necesariamente más fácil.
Veremos que hay técnicas triviales, y otras que requieren más niveles de abstracción o de deducción. Algunas técnicas requieren dos, tres o más deducciones para eliminar candidatos para una casilla. Así podemos clasificar cada técnica en un nivel de dificultad (ya sea para aplicarla o para deducir en qué situación se puede aplicar), y en función de que nivel de técnica sea necesario usar para alcanzar la solución, así se podrá clasificar la dificultad del sudoku.
Resolución
Hay un montón de técnicas de resolución de sudokus. Y aunque nunca hayas aprendido técnicas de otras personas, la práctica te hace descubrir muchas de ellas, y generalmente son suficientes para resolver los sudokus hasta cierto nivel.
Como programador, después de un tiempo resolviendo sudokus, empecé a plantearme cómo resolverlos automáticamente, y cómo generarlos.
Entendámonos, resolverlo por ordenador es relativamente simple, el programa necesario sólo requiere algunas decenas de líneas para resolverlo usando la fuerza bruta. Lo interesante es resolverlo aplicando las mismas técnicas que usaría una persona.
Esta manera de afrontar la tarea tiene dos ventajas claras (para mi):
- Permite afianzar mis técnicas de resolución, y probablemente inventar o buscar y aprender algunas nuevas.
- Permite clasificar por dificultad los sudokus con un criterio fiable.
Adicionalmente puede tener otra aplicación. Podemos generar sudokus aleatoriamente, y verificar si se pueden resolver y en ese caso, clasificarlos por dificultad. Ignoro si es así como se generan en las aplicaciones, pero me apetece intentarlo.
Técnicas triviales
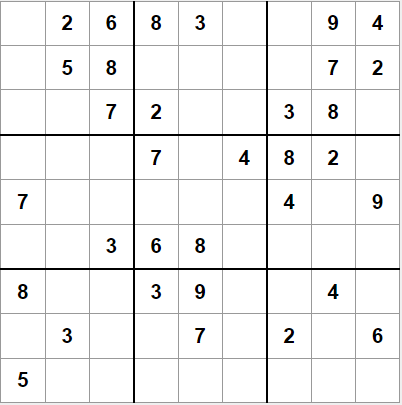
Entre las técnicas que podemos considerar triviales tenemos las que podemos descubrir fácilmente las primeras veces que resolvemos este juego. Empezaremos por uno de la categoría "fácil".
Nos fijamos en la primera casilla, arriba a la izquierda. No puede contener un 2, 3, 4, 6, 8 o 9, ya que esos valores están en la misma fila. Tampoco el 5 o el 7 , que está en la misma columna. Por lo tanto solo puede contener el 1.
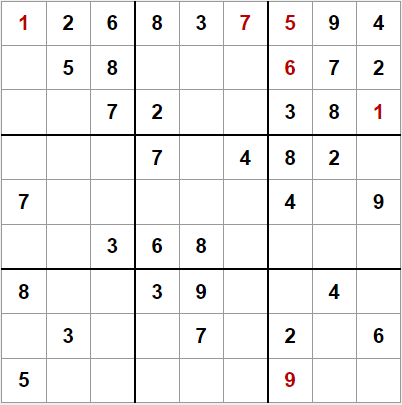
Esta puede ser nuestra primera técnica trivial: si en la fila, columna y caja de una casilla vacía aparecen todos los valores excepto uno, ese será el valor de la casilla.
Aplicando esta técnica podemos colocar algunos números más.
Sin embargo, a no ser que el sudoku sea realmente fácil, esta técnica no nos servirá siempre. Es más, esta técnica será más usada cuando el juego esté casi terminado.
Fijémonos ahora en la primera casilla de la segunda fila. Faltan los valores 3, 4 y 9, y aparentemente no podemos eliminar ninguno, ya que faltan en la segunda fila, en la primera columna, y en la primera caja.
Pero si buscamos el 3 vemos que aparece en la primera fila, en la quinta columna, y el la tercera fila, en la séptima columna. Cada uno de ellos nos da una pista para obtener el valor de la casilla:
- El primero nos dice que en la segunda caja ninguna de las casillas libres puede contener un 3, en concreto, las tres casillas de la segunda fila de esa caja no pueden tener un 3, por lo que solo queda una casilla en la que puede colocarse: la nuestra.
- El segundo nos dice que las casillas libres de la tercera fila no puede haber un 3, es concreto, en las dos casillas libres de la tercera fila de la primera caja no puede haber un 3, lo que solo nos deja una casilla donde puede colocarse: de nuevo, la nuestra.
Esta podría ser nuestra segunda técnica trivial: buscar filas o columnas que eliminen candidatos de todas las casillas libres de una caja, excepto una.
Estas dos reglas bastan para resolver este sudoku.
Pero pronto descubriremos que estas técnicas no son muy efectivas, sobre todo con sudokus más difíciles, porque habrá muchas casillas libres, lo que implica muchos candidatos para cada casilla, y muchas casillas a verificar.
Veamos ahora una técnica simple que, en el peor de los casos, reduce los candidatos para ciertas casillas.
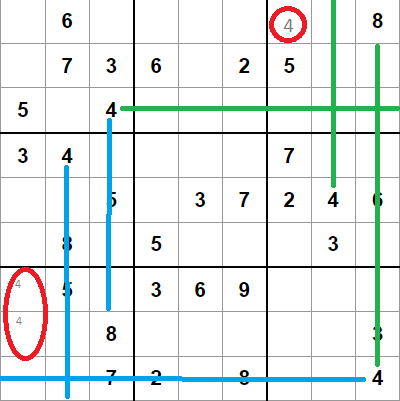
En una primera etapa buscaremos casillas con candidatos únicos, o candidatos que solo aparezcan en dos casillas de la misma fila, columna o caja.
En el ejemplo de la derecha vemos en verde que los 4 en la tercera fila, y en la octava y novena columna solo dejan una casilla en la tercera caja donde es posible colocar un 4.
En el caso de valores que aparezcan en dos casillas haremos lo que se conoce como "marcas de lápiz", es decir, colocar el valor en la casilla, pero de forma provisional, y con un tamaño menor.
En azul vemos que los 4 en la segunda y tercera columna y en la novena fila solo dejan dos casillas en la séptima caja. Marcaremos "en lápiz" esas dos casillas con 4.
La idea de esta técnica es que si tenemos marcadas las dos casillas en la misma fila, columna o caja en las que se puede colocar un número, y posteriormente podemos eliminar una de ellas. La otra será automáticamente un valor final, independientemente de que haya otros candidatos posibles.
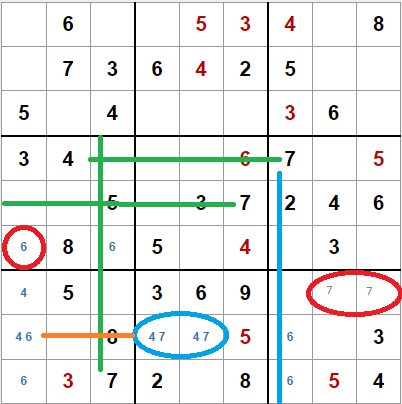
En la siguiente imagen hemos avanzado con esta técnica y vemos algunas ventajas:
- En verde, los 7 de las filas cuarta y quinta y de la tercera columna sólo dejan una casilla en la cuarta caja en la que colocar el 7. Pero esto hace que la pareja de 6 que teníamos marcada ahora solo deja una casilla para ese valor, en la tercera columna y sexta fila.
- Fijémonos ahora en la pareja de casillas marcadas en azul. Las dos tienen como candidatos el 4 y el 7. Además, las dos casillas con el candidato 7 es lo que se denomina una pareja puntero. Estas parejas implican que ese valor no puede aparecer en ninguna casilla de la misma fila (si la pareja puntero está en una fila) o en la misma columna (si la pareja está en la misma columna). Podemos usar esa pareja puntero, junto con el 7 de la novena fila y el de la séptima columna para descubrir otra pareja de 7 en la novena caja.
- La misma pareja contiene una pareja puntero con el 4, por lo que podemos eliminar el 4 como candidato en la primera columna y octava fila.
Veremos más tarde que estas parejas son muy interesantes. Se denominan "parejas desnudas", y cuando aparecen permiten eliminar los valores de la pareja en la columna, fila o caja en la que aparezcan.
Por ésta última técnica, en la octava caja solo queda un valor posible para la casilla libre de la novena fila, el 1.
Resoluble
Antes de pasar a técnicas más complejas, empecemos a programar.
Lo primero que nos interesa, antes de lanzarnos a resolver el sudoku, es saber si tiene solución, y si esa solución es única.
Para ello no usaremos las mismas técnicas que se usan al jugar normalmente, sino que aprovecharemos la capacidad de cálculo del ordenador para encontrar todas las soluciones posibles.
La idea es usar un algoritmo recursivo. Iremos probando con cada número en cada casilla libre mientras se cumplan las reglas. Si llegamos al final y no se ha quebrantado ninguna, añadiremos una solución a la cuenta, si en algún momento un casilla contiene un valor no válido, probaremos con el siguiente, y si se agotan los valores, retrocederemos a la casilla anterior, haciendo 'backtraking' y probaremos con el siguiente candidato.
Para simplificar la aplicación de reglas definiremos varias clases:
- Casilla: encapsula una única casilla. Para empezar almacenará el valor actual. En cuanto a métodos, tendremos un constructor por defecto, un método para asignar un valor a la casilla, otro para recuperar el valor actual, y otro para mostrar el valor en pantalla.
- Fila: encapsula una única fila. Almacenará un array de nueve punteros a Casilla. Tendrá un constructor por defecto y los métodos para: iniciar el array, verificar si un valor está presente en la fila.
- Columna: encapsula una única columna. Almacenará un array de nueve punteros a Casilla. Tendrá un constructor por defecto y los métodos para: iniciar el array, verificar si un valor está presente en la columna.
- Caja: encapsula una única caja. Almacenará un array de nueve punteros a Casilla. Tendrá un constructor por defecto y los métodos para: iniciar el array, verificar si un valor está presente en la caja.
- Tablero: encapsula el sudoku completo. Almacenará un array de 9x9 Casillas, un array de 9 Filas, otro de 9 Columnas y otro de 9 Cajas. También un entero con el contador de soluciones. Tendremos un constructor, que iniciará el sudoku a partir de un array de 81 enteros, y métodos para obtener una referencia a una casilla, para obtener el valor del contador de soluciones, otro para mostrar el tablero, otro para calcular el número de soluciones y otro para verificar si un valor es válido para una casilla.
A medida que el programa avance iremos añadiendo nuevos datos y métodos a cada clase.
Más abajo se puede descargar el programa completo, pero veamos el método Soluciones:
bool Tablero::Soluciones() {
int f, c, n, s;
for(f=0; f<9; f++) {
for(c=0; c<9; c++) {
if(casilla[f][c].Valor() == 0) {
for(n=1; n<=9; n++) {
if(Valido(f, c, n)) {
casilla[f][c].Asignar(n);
if(Soluciones()) return true;
else casilla[f][c].Asignar(0);
}
}
return false;
}
}
}
cuenta++;
return false;
}
El método Valor de casilla obtiene el valor actual de la casilla en la fila f y la columna c,
El método Valido verifica si el valor n cumple las reglas del sudoku para la fila f y la columna c.
El método Asignar de casilla asigna el valor del parámetro a la casilla para la fila f y la columna c.
El método es recursivo, se asigna un valor a cada casilla libre y se invoca al mismo método de nuevo. El valor de retorno indica si debemos continuar con la siguiente casilla libre, si es true, o si debemos retroceder (backtraking) y probar otro valor.
Si un valor asignado a una casilla, a pesar de ser válido, no conduce a una solución, se vacía esa casilla y se prueba el siguiente valor, o si no quedan valores, se retrocede a la casilla anterior con un nuevo valor.
Si el valor conduce a una solución válida, incrementamos la cuenta y retornamos false, con lo que continuamos buscando soluciones.
El programa de ejemplo prueba con un tablero almacenado en una cadena de caracteres 'tablero', en las que el valor de las filas de casillas se almacenan consecutivamente, y el valor '0' indica una casilla vacía. Esta forma es estándar en muchas páginas relacionadas con sudokus. Puedes hacer pruebas con diferentes tableros, eliminar o añadir algún valor y ver qué resultados se obtienen.
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Sudoku1 | sudoku1.zip | 2022-06-22 | 1525 bytes | 629 |