Raíces cuadradas algoritmos

Aunque los lenguajes de programación y los procesadores actuales disponen de mecanismos para calcular raíces cuadradas, no está de más conocer algunos de los algoritmos que permiten calcularlas usando solo operaciones básicas, como sumas, restas, multiplicaciones y divisiones.

En este artículo veremos el algoritmo más conocido para el cálculo de raíces cuadradas: el algoritmo babilónico o Newton-Raphson.

Nuestro objetivo nunca será calcular el valor de la raíz exacto, ya que esto no será posible en la mayor parte de los casos. Esto es debido a que la codificación de números en coma flotante no permite una precisión absoluta. Por ello normalmente ajustaremos el valor de la raíz hasta que el error sea menor de cierta cantidad. Por ejemplo, si queremos tres dígitos decimales estableceremos un valor de error máximo de 0.0001.

Dado que este es un algoritmo de aproximaciones sucesivas, es decir, en cada iteración obtendremos un resultado más preciso, otra alternativa es repetir el algoritmo hasta que obtengamos dos veces consecutivas el mismo valor. De este modo obtendremos el valor más preciso que se puede obtener con el tipo en coma flotante que estemos usando.

Algoritmo

En su forma más primitiva, el algoritmo babilónico se basa en el hecho de que el valor de cada lado de un cuadrado es la raíz cuadrada de su área.

La idea es partir de un rectángulo cuya área (b·h) sea el valor del que queremos obtener la raíz cuadrada (x). Elegiremos un valor arbitrario para b, y calcularemos h como x/b. Posteriormente iremos reduciendo el valor del lado mayor y aumentando el del lado menor hasta que la diferencia sea menor al valor error deseado, pero no ajustaremos esos valores de cualquier forma.

Para hacerlo, calculamos en nuevo valor de b' como (h+b)/2, y el nuevo valor de h' como x/b'.

Repetiremos este paso hasta que la diferencia entre b y h sea menor que el valor de error deseado. Esto es cuando el algoritmo se ejecuta de forma manual, pero cuando se implementa el algoritmo en un programa podemos repetir hasta que obtengamos dos veces consecutivas el mismo valor de b.

Si por ejemplo, queremos calcular la raíz cuadrada de 3790, podemos partir de un rectángulo de 379 x 10.

En cada iteración nos iremos acercando al valor de la raíz cuadrada:

1. b' = (379+10)/2=194.5, h' = 3790/194.5=19.4858.
2. b' = 106.9929, h' = 35.4229.
3. b' = 71.2079 y h' = 53.2244.
4. b' = 62.2162 y h' = 60.9166.
5. b' = 61.5664 y h' = 61.5596.
6. b' = 61.5630 y h' = 61.5629.
7. b' = 61.5630 y h' = 61.5629.

Algoritmo de Newton-Raphson

El algoritmo de Newtos-Raphson es más general, y normalmente se usa para trazar gráficas de funciones, ya que permite obtener las raíces, que son los puntos de corte con el eje x. Si f(x) es una función, las raíces son los valores de x para los cuales f(x)=0.

Se trata de un método abierto, es decir, no se puede garantizar la convergencia. Esto implica que tendremos que partir de un valor inicial aproximado al valor de la raíz. Si por ejemplo, nuestra función tiene tres raíces, tendremos que buscar un valor cercano al de la raíz que estamos buscando, o de otro modo podríamos obtener el valor de otra de las raíces, o en el peor caso, no llegar a ningún valor en absoluto.

El algoritmo se basa en que el valor de la derivada de una función para un valor x es la pendiente de la recta tangente a la función en ese punto.

Para definir una recta solo necesitamos conocer su pendiente y un punto por donde pase. La función general de una recta con una pendiente m y que pasa por el punto (x₀, y₀) es:

$$f\left(x\right)-y_0=m(x-x_0)$$

En nuestro ejemplo, la función de esa recta tangente t es:

$$t\left(x\right)-f\left(x_0\right)=f^{\text{'}}\left(x_0\right)·(x-x_0)$$

Ya que la pendiente es el valor de la derivada de la función en el punto (x₀, f(x₀)), y la recta debe pasar por ese mismo punto.

Esa recta tangente cortará el eje x en un punto más cercano a la raíz buscada más cercana al valor de x elegido. Ahora podemos repetir este proceso tantas veces como sea necesario, dependiendo de la precisión que queramos obtener.

El nuevo valor aproximado es el punto de corte de esa recta con el eje x, por lo tanto, tendremos que igualar esa función a cero y calcular el valor de x:

$$t\left(x\right)=f^{\text{'}}\left(x_0\right)·(x-x_0)+f\left(x_0\right)=0$$

Y despejando el valor de x:

$$f^{\text{'}}\left(x_0\right)·x-f^{\text{'}}\left(x_0\right)·x_0+f\left(x_0\right)=0$$
$$f^{\text{'}}\left(x_0\right)·x=f^{\text{'}}\left(x_0\right)·x_0-f\left(x_0\right)$$
$$x=\frac{f^{\text{'}}\left(x_0\right)·x_0-f\left(x_0\right)}{f^{\text{'}}\left(x_0\right)}$$
$$x=x_0-\frac{f\left(x_0\right)}{f^{\text{'}}\left(x_0\right)}$$

Generalizando, para obtener el valor de x_n+1 a partir de x_n usaremos la fórmula:

$$x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\text{'}}\left(x_n\right)}$$

Pongamos por ejemplo la función:

$$f\left(x\right)=x^3+3x^2-1$$

Su representación gráfica es:

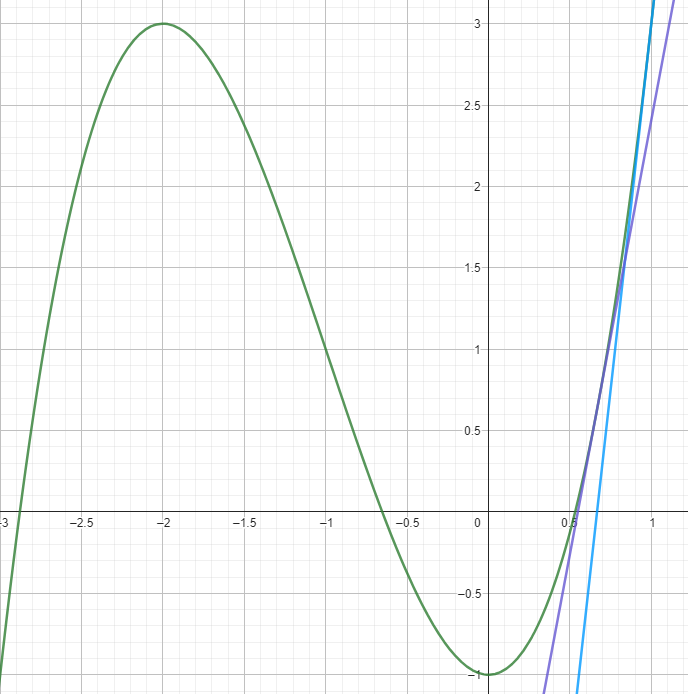
Podemos ver que hay tres raíces, uno cerca de -3, otra cerca de -0.5 y otra cerca de 0.5.

Si partimos de un valor cercano a 0.5, o mayor, el método nos aproximará al valor de la tercera raíz. Si elegimos un valor cercano a -0.5, al de la segunda raíz, etc.

Sin embargo, si seleccionamos un valor correspondiente a un máximo o a un mínimo, por ejemplo, -2 o 0, no obtendremos ninguna raíz, ya que en esos puntos la pendiente es 0, y la recta tangente no corta el eje x.

Si partimos del valor 1, la tangente se muestra en color azul, corta el eje x en el punto 0.666667.

Usando ese valor como segunda aproximación obtenemos otra tangente, ahora en color violeta, que corta el eje x en el punto 0.548618.

Repitiendo el proceso nos acercaremos cada vez más al valor de la raíz, 0.532088.

Raíz cuadrada

De modo que obtener una raíz cuadrada no deja de ser un caso particular.

Nuestro objetivo es obtener el valor de la raíz cuadrada de un número m:

$$x=\sqrt{m}$$

O lo que es lo mismo:

$$x^2=m$$
$$f\left(x\right)=x^2-m$$

Es decir, tendremos que encontrar las raíces de la función f(x), o sea:

$$f\left(x\right)=x^2-m=0$$

Aplicamos la fórmula anterior: $$x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\text{'}}\left(x_n\right)}$$

La derivada de la función f(x) es:

$$f\left(x\right)=2x$$

Por si no lo recuerdas o no lo sabes, la derivada de una potencia de x, x^z es z · x, y la derivada de una constante es cero, de modo que la derivada de x² - n es 2x.

Nuestra fórmula para calcular lar raíces de f(x) es:

$$x_{n+1}=x_n-\frac{{x_n}^2-m}{2·x_n}$$

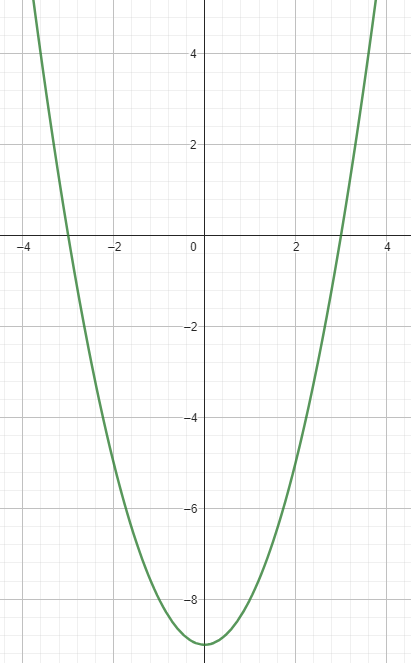
Pongamos que queremos calcular la raíz cuadrada de 9. Nuestra fórmula f(x) será:

$$f\left(x\right)=x^2-9=0$$

Y para obtener sucesivas aproximaciones del valor de la raíz, usaremos la fórmula:

$$x_{n+1}=x_n-\frac{{x_n}^2-9}{2·x_n}$$

Solo nos queda elegir un valor incial para x_n. Ahora hay que fijarse en dos cosas:

1. La función f(x) = x² - n es una parábola, que como no contiene ningún elemento con el factor x, tendrá un valor mínimo para el valor de x=0 y que vale -n.
2. Existen dos raíces, que tendrán el mismo valor absoluto y signos contrarios.

Eso significa que no podemos tomar como valor inicial el valor 0, ya que es un mínimo de la función, y la pendiente de la tangente en ese punto es 0, por lo tanto corresponde a la recta x=-n, que no corta el eje x, y que no nos permite hacer aproximaciones sucesivas.

Si usamos como valor inicial cualquier valor mayor que 0, el método convergerá a la raíz positiva, y si elegimos un valor inicial menor que 0, el método convergerá a la raíz negativa. En general optaremos por valores positivos.

Podemos usar el mismo método para obtener una aproximación imprecisa que con el algoritmo babilónico.

Ambos algoritmos son similares, de hecho, las fórmulas son idénticas. Para el algoritmo babilónico tenemos:

$$x_{n+1}=\frac{h+x_n}{2}$$
$$h=\frac{m}{x_n}$$
$$x_{n+1}=\frac{\frac{m}{x_n}+x_n}{2}$$
$$x_{n+1}=\frac{x_n}{2}+\frac{m}{2·x_n}$$

Y para el algoritmo Newton-Raphson:

$$x_{n+1}=x_n-\frac{{x_n}^2-m}{2·x_n}$$
$$x_{n+1}=x_n-\frac{{x_n}^2}{2·x_n}+\frac{m}{2·x_n}$$
$$x_{n+1}=x_n-\frac{x_n}{2}+\frac{m}{2·x_n}$$
$$x_{n+1}=\frac{x_n}{2}+\frac{m}{2·x_n}$$

Optimizaciones

Podemos optimizar el algoritmo si elegimos mejor el valor inicial de b, es decir, si disponemos de un método para obtener el valor de la raíz cuadrada aunque sea de forma imprecisa, siempre que nos de un valor más aproximado.

Para ello podemos usar lo que se denomina una estimación imprecisa. Se puede aproximar el valor de raíz de x como 3^D, donde D es el valor del número de dígitos de x, y si x es menor de uno, el número de ceros inmediatamente a la derecha del punto decimal.

Si x es 3790, D es 4 y 3⁴ vale 81, que es un valor más razonable para b que 379, y para el que h tomará el valor 46.7901.

Si x es 0.0003790, D es 3 y 3^-3 vale 1/27. Recordemos que x^-n es lo mismo que 1/xⁿ.

Otra posible aproximación, mejor que la anterior, es b=2·10ⁿ, cuando D sea impar, donde n=(D-1)/2, o b=6·10ⁿ, cuando D sea par, donde n=(D-2)/2.

En este caso, para un valor de x igual a 3790, donde D=4 es par, n=(D-2)/2=1, b=6·10¹=60, lo que nos da un valor para h=63.1667.

En cualquiera de los dos casos, tenemos que calcular el valor de D, para lo que tendríamos que usar logaritmos, o un bucle de multiplicaciones o divisiones por 10, dependiendo de si el número es mayor o menor que 1. Al final, se requieren más operaciones. Estos métodos están pensados para calcular raíces manualmente, ya que contar dígitos o decimales, y usar operaciones sencillas: sumas, restas, multiplicaciones y divisiones, es mucho más fácil que calcular raíces cuadradas.

En procesadores antiguos, donde no estaban disponibles operaciones complicadas, a veces ni siquiera multiplicaciones y divisiones, estos cálculos se hacían en base 2, donde contar dígitos es trivial cuando se usa float, ya que uno de los valores que se almacena es precisamente el exponente.

Con fines didácticos, en el siguiente ejemplo se incluye un método para calcular D y el valor inicial aproximado de la raíz.

El ejemplo requiere que se indique un valor de error, pero como alternativa se puede limitar el número de iteraciones, o detener el bucle cuando se obtenga el mismo valor de la raíz en dos iteraciones consecutivas.

#include <iostream>
#include <cmath>

int Digitos(double x);
double Estimacion(double m);
double Babilonico(double m, double error);
double Newton(double m, double error);

int main()
{
    double m = 156465245.56;
    double error = 0.1;

    std::cout << "Metodo de Newton-Raphson" << std::endl;
    std::cout << "Raiz de " << m << " = " << Newton(m, error) << std::endl;

    std::cout << "Metodo Babilonico" << std::endl;
    std::cout << "Raiz de " << m << " = " << Babilonico(m, error) << std::endl;

    std::cin.get();
    return 0;
}

int Digitos(double x) {
    return std::log10(x);
}

double Estimacion(double m) {
    int D = Digitos(m);
    int n; // Valor estimado
    double e;
    if(D%2) {
        n = (D-1)/2;
        e = 2;
    } else {
        n = (D-2)/2;
        e = 6;
    }
    if(n>0) for(int x = 0; x<n; x++) e *= 10;
    else for(int x = 0; x>n; x--) e /= 10;
    return e;
}

double Babilonico(double m, double error) {
    double b=Estimacion(m);
    double h=m/b;

    while(std::fabs(b*b-m) > error) {
        b = (h+b)/2;
        h=m/b;
        std::cout << ".";
    }
    std::cout << " ";
    return b;
}

double Newton(double m, double error) {
    double r = Estimacion(m);

    while(std::fabs(r*r-m) > error) {
        r=r-(r*r-m)/(2*r);
        std::cout << ".";
    }
    std::cout << " ";
    return r;
}

Bibliografía

Wikipedia.

Aproximación del cálculo de la raíz cuadrada mediante una serie.