Algebra de Boole (2)
Métodos tabulares de simplificación
Existen varios métodos de simplificación de funciones tabulares. En este artículo estudiaremos dos de ellos: los mapas de Karnaugh y el Algoritmo de Quine-McCluskey.
Mapas de Karnaugh
El método tabular de simplificación más conocido y usado es el de los mapas de Karnaugh.

Maurice Karnaugh, ingeniero eléctrico. Durante el periodo entre 1952 y 1966 trabajaba en los laboratorios Bell, y en 1954 inventó el método de simplificación de funciones booleanas que llevan su nombre.
Este método sirve para simplificar funciones de hasta seis variables de entrada, (aunque a mi sólo me explicaron hasta cuatro).
Existe un mapa para cada tipo de función, según el número de entradas.
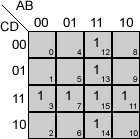
Mapas de Karnaugh para 2, 3 y 4 variables de entrada:
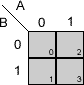
Rellenar un mapa de Karnaugh
Para rellenar el mapa de Karnaugh correspondiente a una función, primero elegiremos el mapa adecuado al número de variables, y después, trasladaremos lo valores de los minterms a las posiciones adecuadas en el mapa, poniendo un '1'.
A veces, existen ciertas combinaciones de las variables de entrada que no se pueden dar en ningún caso real (veremos esto en algunos ejemplos). Para esos casos, la salida de la función puede quedar indeterminada, es decir, no nos importará si el valor de la función para esas combinaciones es uno o cero.
Esto nos puede ayudar a simplificar la función, y trasladaremos esas combinaciones al mapa poniendo una 'X' en las casillas correspondientes.
Un ejemplo
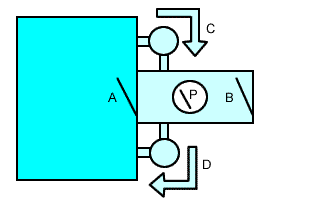
Tenemos que diseñar un sistema de control que permita el paso de personas desde un laboratorio lunar al exterior, y viceversa. Esto se hace mediante un sistema de esclusas, de modo que la presión a ambos lados de la puerta que se quiera abrir sea la misma.
Para poder controlar todas las posibilidades, disponemos de tres señales de entrada:
- a: Petición de apertura de puerta A.
- b: Petición de apertura de puerta B.
- P: Presión de la cámara estanca.
Las funciones que tenemos que obtener son cuatro:
- A: Permiso para abrir la puerta A.
- B: Permiso para abrir la puerta B.
- C: Puesta en marcha de la bomba C.
- D: Puesta en marcha de la bomba D.
El funcionamiento es el siguiente. Una persona dentro del laboratorio quiere salir. Solicita la apertura de la puerta A. Si la presión en la cámara estanca es igual a la del laboratorio (1), se activa la apertura de la puerta A, si la presión es la del vacío (0), no se activa la puerta, pero se activa la bomba C, para igualar la presión de la cámara con la del laboratorio.
El funcionamiento para la otra puerta es análogo. Del mismo modo, las funciones para dar permisos para abrir puertas son las mismas independientemente del lado de la puerta desde el que se pida permiso.
Las tablas de verdad para todas las combinaciones posibles de las tres señales son:
| a | b | P | A | B | C | D |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Hemos decidido que si se pide la apertura de ambas puertas simultáneamente, el sistema permita abrir aquella para la que no haga falta presurizar o despresurizar la cámara estanca.
También podríamos añadir otra condición: que en el laboratorio sólo hay una persona, y por lo tanto, es imposible que se solicite la apertura de ambas puertas de forma simultánea. Las tablas de verdad, teniendo en cuenta esto, serían:
| a | b | P | A | B | C | D |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | X | X | X | X |
| 1 | 1 | 1 | X | X | X | X |
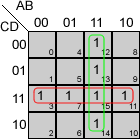
Veamos los mapas de Karnaugh correspondientes a las funciones A, B, C y D, para esta segunda versión:
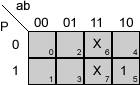
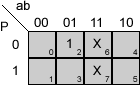
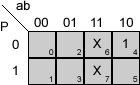
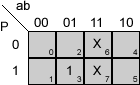
Simplificar un mapa de Karnaugh
Para simplificar un mapa, lo primero que hay que hacer es agrupar de forma gráfica las casillas con unos. Hay varias condiciones que se deben cumplir:
- Los grupos tienen que tener un número de casillas que sea potencia de 2, es decir, 1, 2, 4, 8 ó 16 casillas.
- Sólo se pueden agrupar casillas adyacentes, pero hay que tener en cuenta que en todos los mapas, las adyacencias también se producen entre la parte izquierda y derecha del mapa, y entre la parte superior e inferior.
- La misma casilla puede integrarse en varios grupos, pero todas las casillas con unos deben pertenecer a algún grupo.
- Para completar grupos se pueden incluir casillas con X.
El objetivo es obtener el menor número de grupos que contengan a todas las casillas con unos.
Por cada grupo se obtiene un término de la función de salida. Ese término corresponde a un minterm del que se eliminan las variables que cambian de valor en el grupo. De las variables que quedan, las que tengan valor "1" se incluyen en el minterm sin negar, y las que tengan valor "0", se incluyen negadas.
Simplificar los mapas del ejemplo
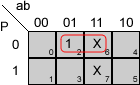
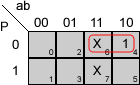
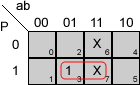
Grupos para las funciones del ejemplo:
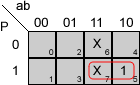
En la función A, tenemos un único grupo en el que debemos eliminar la variable b. Las dos variables que quedan, a y P, valen "1", por lo que se incluyen en el minterm sin negar. La función queda:
A = a·P
Aplicando las mismas reglas a las otras tres funciones:
B = b·P'
C = a·P'
D = b·P
Si tuviéramos que incluir estas funciones en un programa C++, podría quedar algo como:
if(a && P) AbrirPuerta(A); if(b && !P) AbrirPuerta(B); if(a && !P) ActivarBomba(C); if(b && P) ActivarBomba(D);
Ejemplo sentencia if
Antes obtuvimos una tabla de verdad para una función que provenía de una sentencia if. Vamos a aplicar este método para simplificarla:
| A | B | C | D | F |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Tenemos que usar un mapa de cuatro variables, lo rellenamos según esta tabla:
Ahora hacemos los grupos:
En el grupo rojo, las variables C y D desaparecen del minterm, y las variables A y B se incorporan sin negar.
En el grupo verde, las variables A y B desaparecen y quedan las variables C y D sin negar.
El resultado es:
F = A·B + C·D
Que es el punto de partida, por lo que no se ha podido simplificar la función, aunque si partiéramos de la tabla de verdad, es una mejora con respecto a las formas canónicas.
BCD a 7 segmentos
Vamos con el ejemplo clásico para este tipo de problemas.


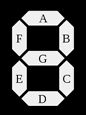
En electrónica se usan dispositivos como el de la figura para mostrar números. A estos dispositivos se les suele llamar displays de siete segmentos, precisamente porque disponen de siete segmentos, de modo que encendiendo algunos de ellos se consiguen mostrar los diez dígitos de la numeración en base 10, es decir, los dígitos '0' a '9'.
Las combinaciones de los segmentos para conseguir cada dígito son las de la figura de la derecha, y a cada segmento se le asigna una letra, de la 'A' a la 'G':
El problema consiste en diseñar las siete funciones, una para cada segmento, en función de las cuatro variables de entrada correspondientes a un dígito BCD, o sea, decimal codificado en binario.
En la codificación BCD se usan los valores binarios del 0 (0000) al 9 (1001).
Tabla de verdad
La tabla de verdad para un codificador BCD a siete segmentos es:
| a | b | c | d | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | X | X | X | X | X | X | X |
| 1 | 0 | 1 | 1 | X | X | X | X | X | X | X |
| 1 | 1 | 0 | 0 | X | X | X | X | X | X | X |
| 1 | 1 | 0 | 1 | X | X | X | X | X | X | X |
| 1 | 1 | 1 | 0 | X | X | X | X | X | X | X |
| 1 | 1 | 1 | 1 | X | X | X | X | X | X | X |
Mapas de Karnaugh
Veamos los mapas de Karnaugh para estas funciones:
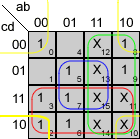
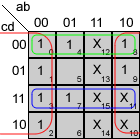
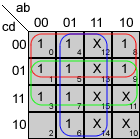
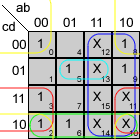
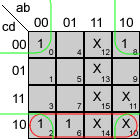
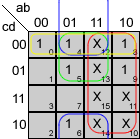
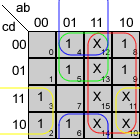
Y las funciones simplificadas quedan:
A = a+c+b·d+b'·d'
B = b'+c·d+c'·d'
C = b+c'+d
D = a+b'·c+b'·d'+c·d'+b·c'·d
E = c·d'+b'·d'
F = a+c'·d'+b·c'+b·d'
G = a+b'·c+b·c'+b·d'
Prueba
Algoritmo de Quine-McCluskey

Edward J. McCluskey, ingeniero eléctrico y profesor, durante el periodo entre 1955 y 1959 trabajaba en los laboratorios Bell. Desarrolló el algoritmo Quine-McCluskey como trabajo de doctorado en el MIT.
El segundo método para simplificar funciones booleanas que veremos es el del algoritmo de Quine-McCluskey. Es algo más laborioso que el de los mapas de Karnaugh, pero tiene dos ventajas importantes:
- No está limitado por el número de variables de entrada. Aunque la complejidad aumenta con cada variable que se añada.
- Es fácilmente programable, con lo que cualquier complejidad derivada del número de variables o de posibles errores queda minimizada.
Primera etapa
Partiremos de la forma canónica de la función, o de su tabla de verdad. El primer paso consiste en obtener la expresión en minterms.
Volvamos a las tablas de verdad del ejemplo del codificador BCD a 7 segmentos:
| a | b | c | d | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | X | X | X | X | X | X | X |
| 1 | 0 | 1 | 1 | X | X | X | X | X | X | X |
| 1 | 1 | 0 | 0 | X | X | X | X | X | X | X |
| 1 | 1 | 0 | 1 | X | X | X | X | X | X | X |
| 1 | 1 | 1 | 0 | X | X | X | X | X | X | X |
| 1 | 1 | 1 | 1 | X | X | X | X | X | X | X |
Esto nos proporciona las siguientes expresiones en mimterms, donde los valores entre paréntesis que siguen a la letra 'm' son los términos minterms de la función, y los que siguen a la letra 'r', los términos redundantes, o sea, los marcados con 'X' en la tabla de verdad:
A = m(0,2,3,5,6,7,8,9) r(10,11,12,13,14,15)
B = m(0,1,2,3,4,7,8,9) r(10,11,12,13,14,15)
C = m(0,1,3,4,5,6,7,8,9) r(10,11,12,13,14,15)
D = m(0,2,3,5,6,8,9) r(10,11,12,13,14,15)
E = m(0,2,3,6,8) r(10,11,12,13,14,15)
F = m(0,4,5,6,8,9) r(10,11,12,13,14,15)
G = m(2,3,4,5,6,8,9) r(10,11,12,13,14,15)
Aplicaremos el algoritmo de Quine-McCluskey a la función G.
Trasladamos a una tabla los minterms de la función, incluyendo los redundantes, y los ordenamos por el número de unos que contienen:
| m | bits | primo |
|---|---|---|
| 1 | ||
| 2 | 0010 | |
| 4 | 0100 | |
| 8 | 1000 | |
| 2 | ||
| 3 | 0011 | |
| 5 | 0101 | |
| 6 | 0110 | |
| 9 | 1001 | |
| 10 | 1010 | |
| 12 | 1100 | |
| 3 | ||
| 11 | 1011 | |
| 13 | 1101 | |
| 14 | 1110 | |
| 4 | ||
| 15 | 1111 | |
A cada uno de los elementos de esta tabla lo llamaremos implicante.
Ahora, intentaremos combinar los implicantes de cada grupo con el siguiente, en este caso, los del grupo con un uno con los del grupo con dos unos, los de dos con los de tres, y los de tres con los de cuatro. Para poder combinar dos implicantes, sus representaciones binarias sólo pueden variar en un bit. Los implicantes resultantes de la combinación se añaden a la tabla, sustituyendo el bit que cambia por un '-'.
Los implicantes que no se puedan combinar se denominan implicantes primos, y se marcan con un '*'.
| m | bits | primo |
|---|---|---|
| 1 | ||
| 2,3 | 001- | |
| 2,6 | 0-10 | |
| 2,10 | -010 | |
| 4,5 | 010- | |
| 4,6 | 01-0 | |
| 4,12 | -100 | |
| 8,9 | 100- | |
| 8,10 | 10-0 | |
| 8,12 | 1-00- | |
| 2 | ||
| 3,11 | -011 | |
| 5,13 | -101 | |
| 6,14 | -110 | |
| 9,11 | 10-1 | |
| 9,13 | 1-01 | |
| 10,11 | 101- | |
| 10,14 | 1-10 | |
| 12,13 | 110- | |
| 12,14 | 11-0 | |
| 3 | ||
| 11,15 | 1-11 | |
| 13,15 | 11-1 | |
| 14,15 | 111- | |
El proceso se repite con cada conjunto de grupos de implicantes obtenido. En cada iteración obtenemos, al menos, un grupo menos, hasta que sólo se obtiene un grupo, o ninguno, si todos los implicantes resultan ser primos.
A veces sucede que al combinar dos parejas distintas de implicantes obtenemos el mismo resultado. En ese caso, ninguno de los cuatro implicantes será primo, pero sólo añadiremos uno de los resultados.
Por ejemplo, en el caso anterior, al combinar las parejas (2,3) con (10,11) obtenemos el mismo implicante que al combinar (2,10) con (3,11). Sólo añadiremos una vez el implicante resultante (2,3,10,11), pero consideraremos que ninguno de los implicantes originales es candidato a implicante primo.
Para la siguiente iteración, los implicantes son:
| m | bits | primo |
|---|---|---|
| 1 | ||
| 2,3,10,11 | -01- | * |
| 2,6,10,14 | --10 | * |
| 4,5,12,13 | -10- | * |
| 4,6,12,14 | -1-0 | * |
| 8,9,10,11 | 10-- | |
| 8,9,12,13 | 1-0- | |
| 8,10,12,14 | 1--0- | |
| 2 | ||
| 9,11,13,15 | 1--1 | |
| 10,11,14,15 | 1-1- | |
| 12,13,14,15 | 11-- | |
La siguiente iteración es la última:
| m | bits | primo |
|---|---|---|
| 1 | ||
| 8,9,10,11,12,13,14,15 | 1--- | * |
Entre todos estos implicantes, los únicos que no se pueden combinar con otros, los implicantes primos, son los siguientes:
| m | bits | primo |
|---|---|---|
| 2,3,10,11 | -01- | * |
| 2,6,10,14 | --10 | * |
| 4,5,12,13 | -10- | * |
| 4,6,12,14 | -1-0 | * |
| 8,9,10,11,12,13,14,15 | 1--- | * |
Con esto hemos terminado la primera etapa del algoritmo.
Segunda etapa
A partir de la tabla de implicantes obtendremos una nueva tabla, llamada tabla de elección. Para formar esta tabla usaremos los implicantes primos.
En esta nueva tabla se incluye una 'X' para cada minterm, excluyendo los redundantes, que compone cada uno de los implicantes primos:
| bin | 2 | 3 | 4 | 5 | 6 | 8 | 9 | Esencial |
|---|---|---|---|---|---|---|---|---|
| -01- | X | X | E | |||||
| --10 | X | X | ||||||
| -10- | X | X | E | |||||
| -1-0 | X | X | ||||||
| 1--- | X | X | E |
En esta tabla marcaremos los implicantes primos que contengan minterms que no estén presentes en otros implicantes primos. Llamaremos a esos implicantes primos, implicantes primos esenciales. Por ejemplo, el minterm '3' sólo está presente en el primer implicante primo, por lo tanto, ese implicante es esencial. Del mismo modo, el minterm '5' sólo está presente en el tercero, y el '8' y el '9', en el quinto.
Todos los minterms presentes en los otros dos implicantes primos también están presentes en otros implicantes primos, y por lo tanto, no son esenciales.
Puede suceder, como en este caso, que eligiendo sólo los implicantes primos esenciales no tengamos todos los minterms que componen la función. En este caso nos falta el '6'. Para el siguiente paso marcaremos todos los minterms presentes en implicantes primos esenciales:
| bin | 2 | 3 | 4 | 5 | 6 | 8 | 9 | Esencial |
|---|---|---|---|---|---|---|---|---|
| -01- | X | X | E | |||||
| --10 | X | X | ||||||
| -10- | X | X | E | |||||
| -1-0 | X | X | ||||||
| 1--- | X | X | E |
Para completar esta etapa, deberemos elegir los implicantes primos no esenciales necesarios para que el conjunto final incluya todos los minterms de la función. Ahora no hay un criterio claro para seleccionar implicantes. En el programa que he hecho para acompañar a este artículo se eligen primero los que más 'X' tengan, y si (como en este caso) todos tienen el mismo número de 'X' sin marcar, se elige uno al azar.
Cada vez que elijamos uno, lo marcaremos como esencial, y marcaremos las 'X' que contenga en el resto de los implicantes.
| bin | 2 | 3 | 4 | 5 | 6 | 8 | 9 | Esencial |
|---|---|---|---|---|---|---|---|---|
| -01- | X | X | E | |||||
| --10 | X | X | e | |||||
| -10- | X | X | E | |||||
| -1-0 | X | X | ||||||
| 1--- | X | X | E |
En nuestro ejemplo no quedan 'X' sin marcar, por lo tanto, este proceso ha terminado.
Tercera etapa
El último paso es obtener la fórmula. Para ello usaremos las combinaciones binarias de los implicantes primos esenciales. Cada uno determina un término en minterm reducido, que se debe combinar mediante funciones OR con el resto. Cada bit corresponde a una variable. Las variables correspondientes a bits con un '-' se eliminan de la expresión, las que correspondan a un '1' se incluyen directamente, y las que correspondan con un '0', se incluyen negadas.
De este modo, "-01-" corresponde con b'·c. Y la función G:
G = b'·c + c·d' + b·c' + b·d' + a