Arboles-B

Generalidades

Los árboles-B son árboles de búsqueda.

La "B" probablemente se debe a que el algoritmo fue desarrollado por "Rudolf Bayer" y "Eduard M. McCreight", que trabajan para la empresa "Boeing" aunque parece que "Karl Unterauer" desarrolló un algoritmo semejante en la misma época.

Lo que si es cierto es que la letra B no significa "binario", ya que:

Los árboles-B nunca son binarios.
Y tampoco es porque sean árboles de búsqueda, ya que en inglés se denominan B-trees.
Tampoco es porque sean balanceados, ya que no suelen serlo.

En cualquier caso, tampoco es demasiado importante el significado de la "B", si es que lo tiene, lo interesante realmente es el algoritmo.

A menudo se usan árboles binarios de búsqueda para ordenar listas de valores, minimizando el número de lecturas, y evitando tener que ordenar dichas listas.

Pero este tipo de árboles tienen varias desventajas:

Es difícil construir un árbol binario de búsqueda perfectamente equilibrado.
El número de consultas en el árbol no equilibrado es impredecible.
Y además el número de consultas aumenta rápidamente con el número de registros a ordenar.

Para evitar estos inconvenientes se usan árboles-B, sobre todo cuando se ordenan ficheros, donde se ha convertido en el sistema de indexación más utilizado. En el curso sobre manejo de ficheros veremos una implementación de árboles-B aplicaco a ficheros.

Los árboles-B son árboles de búsqueda de m ramas, y cada nodo puede almacenar un máximo de m-1 claves.

Las características que debe cumplir un árbol-B son:

Un parámetro muy importante en los árboles-B es el ORDEN (m). El orden de un árbol-B es el número máximo de ramas que pueden partir de un nodo.
Si n es el número de ramas que parten de un nodo de un árbol-b, el nodo contendrá n-1 claves.
El árbol está ordenado.
Todos los nodos terminales, (nodos hoja), están en el mismo nivel.
Todos los nodos intermedios, excepto el raiz, deben tener entre m/2 y m ramas no nulas.
El máximo número de claves por nodo es m-1.
El mínimo número de claves por nodo es (m/2)-1.
La profundidad (h) es el número máximo de consultas para encontrar una clave.

Existen varios criterios para dimensionar el ORDEN de un árbol-B.

Normalmente se intenta limitar la profundidad del árbol, de modo que el número máximo de consultas sea pequeño. Cuanto mayor sea el ORDEN, menor será la profundidad.

Cuando se crean árboles-B para indexar ficheros de datos en disco, intervienen otras condiciones. En ese caso interesa que el número de accesos a disco sea lo más pequeño posible. Para calcular el ORDEN se usa como dato el tamaño del cluster. Un cluster es el bloque de disco más pequeño que se lee o se escribe en una operación de acceso a disco, su tamaño suele ser distinto según el tamaño de disco y el tipo de formato que tenga, puede variar entre 512 bytes y múltiplos de esa cantidad. El ORDEN se ajusta de modo que el tamaño del nodo sea lo más próximo posible, menor o igual, al tamaño del cluster.

Las operaciones que se pueden realizar en un árbol-B son básicamente tres:

Insertar una clave.
Eliminar una clave.
Buscar una clave.

Estructura de un nodo

Para ilustrar este artículo haremos un programa que indexará una tabla de enteros usando un árbol-B.

Implementaremos dos clases, una para el tratamiento de los nodos y otra para el árbol.

Cada clave estará compuesta por una pareja de valores, uno de esos valores es la propia clave, en nuestro ejemplo será un entero, pero en general será del mismo tipo que el campo por el que ordenaremos la tabla o fichero, el otro campo será una referencia al registro al que corresponda dicha clave. Por ejemplo, si tenemos un fichero con la siguiente estructura de registro:

struct registro {
   char nombre[32];
   int edad;
   long telefono;
};

Y queremos construir un árbol-B para indicar una tabla de 1000 registros por el campo nombre.

Nuestra clave será una estructura como ésta:

struct stclave {
   char nombre[32];
   long registro; // número índice correspondiente a la clave "nombre"
};

Si lo que tenemos que ordenar es un fichero, el valor de registro sería la posición del registro de datos asociado a la clave dentro del fichero.

En rigor, un nodo sólo necesita almacenar un máximo de m-1 claves y m punteros, pero para facilitar el manejo de los árboles-B, añadiremos algunos datos extra.

Para el nodo, definiremos la clase bnodo como sigue:

class bnodo {
  public:
   bnodo(int nClaves); // Constructor
   ~bnodo();           // Destructor

  private:
   int clavesUsadas;   // Claves usadas en el nodo
   stclave *clave;     // Array de claves del nodo
   bnodo **puntero;    // Array de punteros a bnodo
   bnodo *padre;       // Puntero a nodo padre

  friend class btree;
};

Además de un array de claves y de punteros, que es lo que se necesita para definir un nodo según el gráfico que hemos visto antes, hemos añadido un par de datos más que nos facilitarán en manejo del árbol.

Uno es el número de claves usadas en el nodo, ya sabemos que no tienen por qué estar todas usadas. El otro es un puntero al nodo padre, este puntero nos será muy útil para insertar y eliminar claves.

Clase para manejar la estructura del árbol:

class btree {
  public:
   btree(int nClv);              // Constructor
   ~btree();                     // Destructor
   long Buscar(int clave);       // Buscar un valor de clave, devuelve la posición en el array
   bool Insertar(stclave clave); // Insertar una clave
   void Borrar(int clave);       // Borrar la clave correspondiente a un valor
   void Mostrar();               // (Depuración) Mostrar el árbol por pantalla

  private:
   stclave *lista;               // Auxiliar para insertar claves
   pbnodo *listapunt;            // Auxiliar para insertar claves
   // Funciones auxiliares internas de la clase:
   void Inserta(stclave clave, pbnodo nodo, pbnodo hijo1, pbnodo hijo2);
   void BorrarClave(pbnodo nodo, int valor);
   void BorrarNodo(pbnodo nodo);
   void PasarClaveDerecha(pbnodo derecha, pbnodo padre, pbnodo nodo, int posClavePadre);
   void PasarClaveIzquierda(pbnodo izquierda, pbnodo padre, pbnodo nodo, int posClavePadre);
   void FundirNodo(pbnodo izquierda, pbnodo &padre, pbnodo derecha, int posClavePadre);
   void Ver(pbnodo nodo);

   int nClaves;                  // Número de claves por nodo
   int nodosMinimos;             // Número de punteros mínimos para cada nodo que no sea hoja
   pbnodo Entrada;               // Puntero a nodo de entrada en el árbol
};

Se han declarado varias funciones auxiliares privadas para facilitar la inserción y borrado de nodos. Estas funciones sólo se usarán internamente por la clase.

Algoritmo de inserción de claves

Se trata de un algoritmo iterativo, aunque también puede implementarse recursivamente.

Buscar la clave en el árbol. (Nuestro algoritmo no permite almacenar claves duplicadas).
Si la clave ya está en el árbol, salimos sin hacer nada.
Buscamos el nodo donde debería añadirse la clave. (nodo)
derecho = izquierdo = NULL
Bucle:
- Si nodo es NULL crear un nodo nuevo y hacer que Entrada sea el nuevo nodo.
- Guardar el valor del padre de nodo en padre.
- ¿Hay espacio libre en nodo para la nueva clave?
  - SI:
    - Almacenar la clave en nodo.
    - Puntero izquierdo = izquierdo.
    - Puntero derecho = derecho.
    - salir de bucle.
  - NO:
    - Crear un nodo nuevo
    - Segregar la mitad de las claves menores en nodo y la mitad de las mayores en nuevo.
    - Promocionar el valor intermedio, es decir insertarlo en el nodo padre.
      - izquierdo = nodo
      - derecho = nuevo
      - nodo = padre
      - clave = clave intermedia
    - cerrar bucle

Veremos ahora algunos ejemplos.

Ejemplo con inserción de nodo

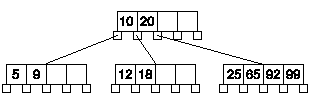
Veamos un ejemplo. Supongamos que queremos insertar la clave 52 en el árbol del ejemplo.

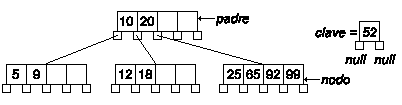
No hay espacio para almacenar la clave en nodo, por lo tanto creamos un nuevo nodo:

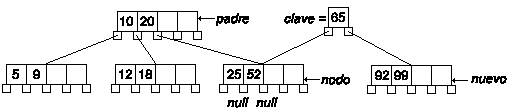
Ahora tenemos que promocionar la clave intermedia, insertándola en el nodo padre. El proceso es recursivo, aunque el algoritmo que hemos diseñado es iterativo.

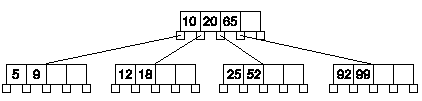
Ejemplo con aumento de altura del árbol

Veamos otro ejemplo que implicará que aumente la altura del árbol. Supongamos que tenemos un árbol con esta estructura, y queremos insertar la clave 68:

En primer lugar, dividimos nodo en dos, repartimos las claves y promocionamos el valor intermedio, el 69:

Ahora estamos de nuevo en la misma situación, el anterior nodo pasa a ser el nodo padre, y el padre de éste es null. Ahora procedemos igual, dividimos nodo en dos, separamos las claves, y promocionamos el valor intermedio:

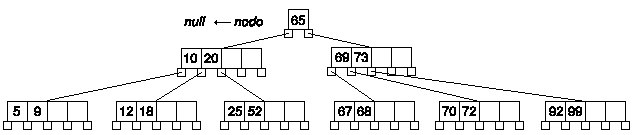
Y otra vez repetimos el proceso, el algoritmo funciona de forma recursiva, pero en este caso nodo es null, por lo tanto estamos en un caso diferente, según el algoritmo debemos crear un nuevo nodo, hacer que ese nodo sea el de entrada, insertar la clave y actualizar los punteros:

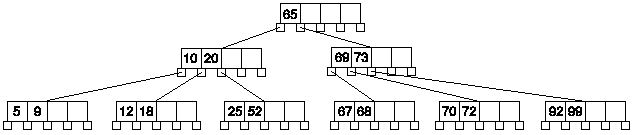
Algoritmo de borrado de claves

Borrar nodos es algo más complicado, como veremos ahora. También se trata de un algoritmo iterativo, aunque puede implementarse recursivamente.

Buscar el nodo donde está la clave que queremos borrar.
Si la clave no está en el árbol, salimos sin hacer nada.
Buscamos la posición que ocupa la clave dentro del nodo.
¿Se trata de un nodo hoja o terminal?
- SI:
  - hoja = nodo
- NO:
  - Intercambiar clave con la clave siguiente. Se trata de la primera clave del nodo hoja obtenido al seguir la rama izquierda a partir del nodo derecho de la clave actual.
  - hoja = nodo de la siguiente clave
Eliminar clave, se consigue rotando las claves siguientes dentro del nodo y decrementando el número de claves usadas del nodo.
Si el número de claves usadas es cero y hoja es el nodo de entrada:
- SI:
  - Entrada = NULL
  - Borrar hoja
  - Salir.
Hoja es el nodo de entrada o el número de claves usadas es mayor del número mínimo de claves por nodo:
- SI:
  - Salir.
Bucle:
- Buscar el puntero que apunta a hoja en nodo padre: posClavePadre.
- Localizar los nodos izquierdo y derecho del nodo hoja.
- Si existe el nodo derecho y contiene más claves que el número mínimo.
  - SI:
    - Pasar una clave del nodo derecho a padre, en posClavePadre y la clave que había allí al nodo hoja.
    - Salir.
- Si existe el nodo izquierdo y contiene más claves que el número mínimo.
  - SI:
    - Pasar una clave del nodo izquierdo a padre, en posClavePadre y la clave que había allí al nodo hoja.
    - Salir.
- Si existe el nodo derecho.
  - SI:
    - Fundir en hoja los nodos hoja y derecho junto con la clave del nodo padre posClavePadre. Borrar nodo derecho.
    - Si padre es el nodo de entrada y no tiene claves.
      - SI:
        
        entrada = hoja
        
        borrar nodo padre
        
        salir
  - NO: (Entonces debe existir un nodo izquierdo)
    - Fundir en izquierdo los nodos hoja y izquierdo junto con la clave del nodo padre posClavePadre. Borrar nodo hoja.
    - Si padre es el nodo de entrada y no tiene claves.
      - SI:
        
        entrada = izquierdo
        
        borrar nodo padre
        
        salir
- hoja = padre
- Si hoja no es NULL, ni hoja es el nodo de entrada ni el número de claves en hoja es menos que el mínimo.
  - SI:
    - cerrar bucle.
  - NO:
    - Salir.

Veremos ahora algunos ejemplos.

Clave en nodo hoja y número de claves mayor que el mínimo

Borraremos la clave 65. Es uno de los casos más sencillos, la clave está en un nodo hoja, y el número de claves del nodo después de eliminarla es mayor del mínimo.

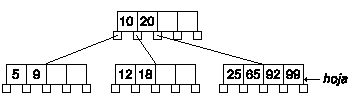
Tan sólo tendremos que eliminar la clave:

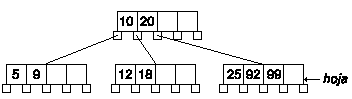
Clave en nodo intermedio

Eliminaremos ahora la clave 20.

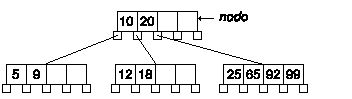
Según el algoritmo debemos intercambiar la clave por el siguiente valor, es decir, el 25. En general será la primera clave del nodo más a la izquierda a de la rama derecha de la clave a borrar.

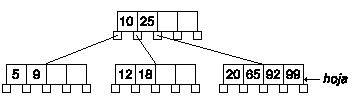
Ahora estamos en el mismo caso que antes, sólo hay que borrar la clave 20 del nodo hoja:

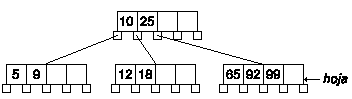
Borrar clave cuando el número de claves es menor que el mínimo

Eliminaremos el nodo 12 del árbol:

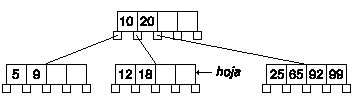
La primera parte es fácil, bastará eliminar la clave, pero el resultado es que sólo queda una clave en el nodo, y debe haber al menos dos claves en un nodo de cuatro.

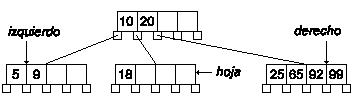
Según el algoritmo, buscaremos los nodos izquierdo y derecho. Si el número de claves en el nodo derecho es mayor que el mínimo, pasaremos una clave del nodo derecho al padre y de éste al nodo hoja. Si no, lo intentaremos con el izquierdo. En este caso nos vale el nodo derecho:

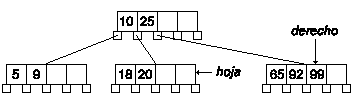
Borrar clave cuando implica borrar nodos

Vamos a ver el caso en que tanto el nodo derecho como el izquierdo no tienen claves suficientes para transferir una al nodo hoja. Borraremos la clave 5:

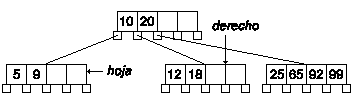
La primera parte es igual que el caso anterior, eliminamos la clave 5. Pero ahora el nodo derecho tiene el número mínimo de claves, y el izquierdo no existe.

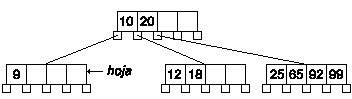
Según el algoritmo, debemos fundir en el nodo hoja, las claves del nodo hoja, la clave del padre y las del nodo derecho. Y después eliminar el nodo derecho.

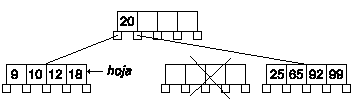
La cosa no termina ahí, ahora debemos comprobar el nodo padre, ya que también ha podido quedar con menos claves que el mínimo exigido. En este caso sucede eso, pero es un caso especial, ya que ese nodo es el de entrada y puede contener menos claves que número mínimo.

Caso de reducción de altura

Veamos cómo sería el proceso en un caso general, que implica la reducción de altura del árbol.

Borraremos la clave 65 de este árbol:

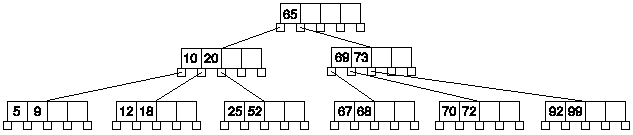
El primer paso es intercambiar la clave 65 por la siguiente, la 67. Y hacer que el nodo al que pertenece sea el nodo hoja:

A continuación eliminamos la clave 65 del nodo hoja, y comprobamos que el nodo tiene menos claves del mínimo. Buscamos el nodo derecho e izquierdo.

El nodo izquierdo no existe, y el derecho tiene justo el número mínimo de claves, por lo tanto tenemos que fusionar hoja con derecho y con una clave de padre. Y eliminamos el nodo derecho.

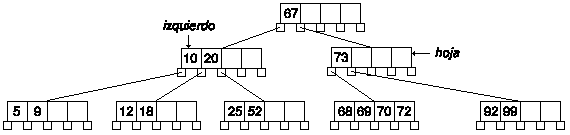
Ahora el nodo hoja es el padre del anterior nodo hoja. De nuevo comprobamos que tiene menos claves que el mínimo, así que buscamos los nodos derecho e izquierdo. Y de nuevo comprobamos que el nodo derecho no existe y que el izquierdo tiene justo el número mínimo de claves.

Ahora fusionamos en el nodo izquierdo con el nodo hoja y con una clave del nodo padre, y eliminamos el nodo hoja, como además el nodo padre es el de entrada y ha quedado vacío, lo eliminaremos y el nodo de entrada será el izquierdo:

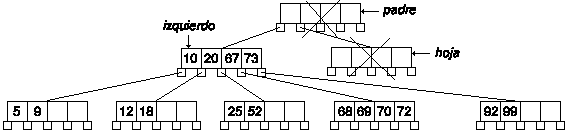
Programa en C++

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Ejemplo Arbol-B	Btree.zip	2001-08-01	11735 bytes	828