12 Conjuntos

Existen más estructuras de datos útiles en programación. En este capítulo veremos los conjuntos o sets.

12.1 Qué son

Los conjuntos, como su nombre indica, son agrupaciones de elementos del mismo tipo de valores únicos.

En lo que respecta al modo en que se almacenan, no difieren mucho de otras estructuras como listas o arrays. Lo que diferencia a un conjunto de otras estructuras de datos son los métodos de que dispone.

Normalmente se implementan como un árbol Rojo-Negro, y entre los métodos que suelen tener se incluyen:

• Vacío: verificar si el conjunto no tiene elementos.
• Tamaño: devuelve el número de elementos.
• Vaciar: elimina todos los elementos.
• Insertar: añade un elemento.
• Borrar: elimina un elemento.
• Encontrar: busca un elemento.

Esto es en lo que respecta a los conjuntos como estructuras de datos, pero en matemáticas existe la "Teoría de conjuntos" que permite cierta aritmética entre conjuntos, y que puede ser interesante añadir a estas estructuras de datos.

Entre esos métodos útiles que por ejemplo, los Set en STL no tienen, tenemos la unión, intersección, diferencia, diferencia simétrica y complemento (cuando se pueda).

Como ya tenemos el código para los árboles Rojo-Negro, podemos obtener el de los conjuntos añadiendo los métodos que faltan.

12.2 Métodos

Veamos cada uno de los métodos, en qué consisten y cómo implementarlos.

12.2.1 Vacío

Hay varias formas de saber si un conjunto está vacío. Como también queremos implementar un método para contar elementos, una forma sería verificar si esa cuenta es cero.

Pero, en general, esa no es la forma óptima de hacerlo. Es más eficiente verificar si el nodo raíz es nulo, en cuyo caso, el conjunto estará vacío. Nuestro código para árboles RN ya dispone de ese método.

12.2.2 Tamaño

Para calcular el número de elementos bastará con recorrer el árbol en cualquier orden, y contar los nodos. Para evitar el uso de la 'ñ', usaremos el término "Cardinalidad".

Nos ayudaremos de una función auxiliar. Por ejemplo, en C:

int Cuenta(pNodo n, int* cuenta)
{
    if(n) {
        (*cuenta)++;
        Cuenta(n->izquierdo, cuenta);
        Cuenta(n->derecho, cuenta);
    }
}

/* Devuelve el número de elementos */
int Cardinalidad(Arbol a) {
    int cuenta = 0;
    Cuenta(a, &cuenta);
    return cuenta;
}

12.2.3 Vaciar

Este método también existe en nuestra implementación del árbol RN. En C se usa para destruir la estructura, en C++ tenemos el método BorrarArbol que es invocado por el destructor.

12.2.4 Insertar

Por supuesto, este método existe en la implementación del árbol RN.

12.2.5 Borrar

Al igual que el método Borrar.

12.2.6 Encontrar

Nuestra implementación del árbol RN dispone de un método Buscar que devuelve un puntero al nodo, si encuentra uno con el valor indicado, o un puntero nulo en caso contrario.

Para los conjuntos cambiaremos este método por uno que devuelve un valor booleano.

Usaremos el identificador Contiene, en lugar de Buscar o Encontrar.

12.3 Operaciones con conjuntos

Para mi, las operaciones más interesantes con conjuntos son las que se definen en la teoría de conjuntos.

En esta teoría, la propiedad de un elemento que está en un conjunto se denomina pertenencia.

El número de elementos se denomina cardinalidad.

Cuando la pertenencia se aplica a conjuntos en lugar de a elementos, tenemos el concepto de inclusión.

Y, por supuesto, tenemos la propiedad de igualdad entre conjuntos.

Además, podemos incluir las operaciones entre conjuntos:

• Unión: sean A y B dos conjuntos. La unión es el conjunto que contiene todos los elementos que están en A o en B o en los dos.
• Intersección: dados los conjuntos A y B la intersección es el conjunto que contiene los elementos que están tanto en A como en B.
• Diferencia: en dos conjuntos A y B la diferencia es el conjunto que contiene los elementos de A que no pertenecen a B.
• Diferencia simétrica: se llama diferencia simétrica entre dos conjuntos A y B al conjunto formado por los elementos de A que no pertenecen a B y los elementos de B que no pertenecen a A, es decir, aquellos elementos que pertenecen exclusivamente a uno de los conjuntos.
• Complementación: se trata de una diferencia entre un conjunto que contenga todos los elementos del dominio, llamado conjunto universal y el conjunto A.

No siempre será posible aplicar el complemento de un conjunto, ya que a menudo el dominio será demasiado grande. Será relativamente fácil si el conjunto universal tiene pocos elementos, como el alfabeto, pero no tiene sentido en conjuntos como los números.

A estas operaciones podemos añadir otras que también pueden ser útiles:

• Igualdad: dados dos conjuntos A y B, serán iguales si contienen los mismos elementos.
• Subconjunto: diremos que A es un subconjunto de B si todos los elementos de A pertenecen a B.
• Superconjunto: diremos que A es un superconjunto de B si todos los elementos de B pertenecen a A.

13.3.1 Diagramas

Para la representación gráfica de conjuntos se suelen usar diagramas de Venn o diagramas de Euler.

Nosotros usaremos los diagramas de Venn para representar las diferentes operaciones entre conjuntos.

Un diagrama de Venn muestra cómo se relacionan dos o más conjuntos. Para ello se utilizan círculos superpuestos. La superposición representa los elementos que comparten y el resto las que no.

13.3.2 Union

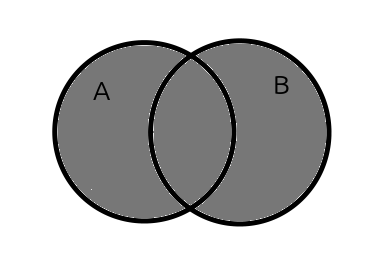
El operador de unión toma como argumentos dos conjuntos A y B y obtiene como resultado otro conjunto.

Para obtener el conjunto de salida, la forma más simple es añadir los elementos de los conjuntos A y B. Los elementos que pertenezcan a los dos conjuntos sólo se añadirán una vez, puesto que nuestro método de inserción ignora los elementos que ya pertenezcan al conjunto.

Para esta tarea necesitamos combinar dos funciones. Una será la propia operación de unión, tomará como argumentos dos conjuntos y devolverá un conjunto con el resultado de la operación.

La segunda función es una función auxiliar que recorrerá un conjunto de entrada en pre-orden añadiendo sus elementos a otro conjunto.

void PreOrdenUnion(Conjunto* U, pElemento n) {
    if(n) {
        Insertar(U, n->valor);
        PreOrdenUnion(U, n->izquierdo);
        PreOrdenUnion(U, n->derecho);
    }
}

Conjunto Union(Conjunto A, Conjunto B) {
    Conjunto U=NULL;

    PreOrdenUnion(&U, A);
    PreOrdenUnion(&U, B);
    return U;
}

Cuando invoquemos la función Union tendremos que tener cuidado de que el conjunto que recibirá el resultado esté vacío. De otro modo se producirá una fuga de memoria, al perder el puntero al nodo inicial del árbol.

    Conjunto U = Union(A, B); // Inicialmente U es un conjunto vacío

13.3.3 Intersección

El operador de intersección toma como argumentos dos conjuntos A y B y obtiene como resultado otro conjunto.

Para obtener el conjunto de salida, la forma más simple es verificar si cada elemento del conjunto A pertenece al conjunto B, y en ese caso añadirlo al conjunto de salida.

Para esta tarea también necesitamos combinar dos funciones. Una será la propia operación de intersección, tomará como argumentos dos conjuntos y devolverá un conjunto con el resultado de la operación.

La segunda función es una función auxiliar que recorrerá uno de los conjuntos de entrada en pre-orden añadiendo sus elementos a otro conjunto si pertenecen al otro conjunto de entrada.

void PreOrdenIntereseccion(Conjunto *U, pElemento n, Conjunto B) {
    if(n) {
        if(Pertenece(B, n->valor)) Insertar(U, n->valor);
        PreOrdenIntereseccion(U, n->izquierdo, B);
        PreOrdenIntereseccion(U, n->derecho, B);
    }
}

Conjunto Interseccion(Conjunto A, Conjunto B) {
    Arbol U=NULL;

    PreOrdenIntereseccion(&U, A, B);
    return U;
}

De nuevo, tendremos que asegurarnos de que el conjunto que recibirá el resultado esté vacío antes de asignarle el resultado de la operación.

    Eliminar(U);
    U = Interseccion(A, B);

13.3.4 Diferencia

Para calcular la diferencia entre dos conjuntos A y B tenemos varias posibles opciones:

• Copiar el conjunto A al conjunto de salida y eliminar los elementos que pertenecen a B del conjunto de salida.
• Copiar el conjunto A al conjunto de salida y eliminar los elementos del conjunto intersección de A y B.
• Recorrer los elementos del conjunto A, si no están en B, añadirlos al conjunto de salida.

Probablemente la mejor opción sea la última, ya que no requiere borrado de elementos.

El código es casi idéntico al de la intersección, la única diferencia es que añadiremos los elementos que no encontremos en B, en lugar de los que encontremos:

void PreOrdenDiferencia(Conjunto *U, pElemento n, Conjunto B) {
    if(n) {
        if(!Pertenece(B, n->valor)) Insertar(U, n->valor);
        PreOrdenDiferencia(U, n->izquierdo, B);
        PreOrdenDiferencia(U, n->derecho, B);
    }
}
Conjunto Diferencia(Conjunto A, Conjunto B) {
    Arbol U=NULL;

    PreOrdenDiferencia(&U, A, B);
    return U;
}

13.3.5 Diferencia simétrica

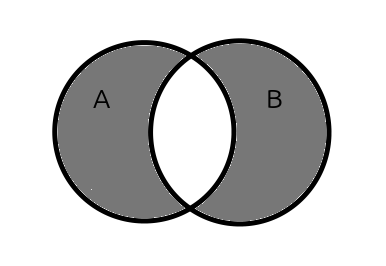
Calcular la diferencia simétrica entre dos conjuntos A y B también se puede hacer de formas diferentes:

• Calcular la diferencia entre la unión y la intersección.
• Calcular la unión entre la diferencia entre A y B y la diferencia entre B y A.

Pero esta no es la forma más eficiente de calcular la diferencia simétrica. En su lugar usaremos el mismo algoritmo que para la diferencia, pero añadiendo la diferencia entre B y A.

Conjunto DiferenciaSimetrica(Conjunto A, Conjunto B) {
    Conjunto U=NULL;

    PreOrdenDiferencia(&U, A, B);
    PreOrdenDiferencia(&U, B, A);
    return U;
}

13.3.6 Complementación

Para esta operación no es necesario crear ninguna función. Cuando para algún conjunto A podamos determinar un conjunto universal con un número de elementos manejable, bastará con definir el conjunto universal, y calcular la diferencia con el conjunto A.

Pero si no podemos crear el conjunto universal, no tendrá sentido usar esta operación.

13.3.7 Igualdad

Para saber si dos conjuntos son iguales podemos calcular su diferencia. Si el resultado es un conjunto vacío, los conjuntos son iguales.

Pero en realidad no necesitamos calcular otro conjunto, bastará con comparar sus cardinalidades. Si son diferentes, los conjuntos son diferentes.

Si tienen la misma cardinalidad, buscaremos los elementos de un conjunto en el otro, si encontramos todos, los conjuntos son iguales, en el momento que no encontremos uno de ellos, podemos decir que son diferentes.

De nuevo nos ayudaremos con una función auxiliar:

void PreOrdenIgualdad(BOOLEAN* retval, pElemento n, Conjunto B) {
    if(!*retval || !n) return;
    if(Pertenece(B, n->valor)) {
        PreOrdenIgualdad(retval,n->izquierdo, B);
        PreOrdenIgualdad(retval, n->derecho, B);
    } else *retval &= FALSE;
}

BOOLEAN Igualdad(Conjunto A, Conjunto B) {
    BOOLEAN retval=TRUE;
    if(Cardinalidad(A) != Cardinalidad(B)) return FALSE;
    else PreOrdenIgualdad(&retval, A, B);
    return retval;
}

13.3.8 Subconjunto

Dados dos conjuntos A y B, diremos que A es un subconjunto de B si todos los elementos de A pertenecen a B.

También se puede expresar como B contiene a A.

El resultado de esta operación, como en el caso de pertenencia o igualdad, es un booleano.

Hay varias formas de implementar esta operación:

• Calcular el conjunto intersección I, de A y B. Si I=A, entonces A es un subconjunto de B. Esto requiere que también definamos un operador de comparación, que verifique si dos conjuntos son iguales.
• Calcular el conjunto unión U, de A y B. Si U=B, entonces A es un subconjunto de B.
• Recorrer todos los elementos de A y verificar si pertenecen a B. En el momento en que uno de los elementos de A no pertenezca a B no necesitaremos seguir comprobando el resto, ya sabremos que A no es un subconjunto de B.

La última forma es la más económica en recursos y tiempo de ejecución, ya que no requiere crear un nuevo conjunto.

Nos podemos basar en el algoritmo para verificar la igualdad, con la diferencia de que no necesitamos comparar las cardinalidades.

BOOLEAN Subconjunto(Conjunto A, Conjunto B) {
    BOOLEAN retval=TRUE;
    if(Cardinalidad(A) > Cardinalidad(B)) return FALSE;
    else PreOrdenIgualdad(&retval, A, B);
    return retval;
}

13.3.9 Superconjunto

Dados dos conjuntos A y B, diremos que A es un superconjunto de B si todos los elementos de B pertenecen a A.

Decir que A es un superconjunto de B es lo mismo que decir que B sea un subconjunto de A. Por lo tanto la implementación es sencilla:

BOOLEAN Superconjunto(Conjunto A, Conjunto B) {
    return Subconjunto(B, A);
}

13.4 Sobrecarga en versiones con clases y plantillas

Vamos a hacer operaciones con conjuntos, y para ello sobrecargaremos algunos operadores.

Esto hará más sencilla la sintaxis de aritmética de conjuntos, de este modo será posible usar expresiones como C=A+B o C=A.Union(B).

La elección de operadores es evidente para la Unión y para la Diferencia, suma y resta.

Para la Intersección podemos usar el operador &. y para la Diferencia simétrica el operador ^, por ejemplo.

Además, al usar memoria dinámica, será imprescindible crear el constructor copia, y útil sobrecargar el operador de asignación.

No usaremos operadores para Pertenencia, Subconjunto o Superconjunto.

13.4.1 Constructor copia

En realidad deberíamos haber sobrecargado este constructor para otras estructuras de este curso, ya que todas usan objetos asignados dinámicamente.

Para hacerlo nos ayudaremos de un método auxiliar privado:

class Conjunto {
   public:
    Conjunto() : raiz(nullptr) {}
    ~Conjunto();
    Conjunto(const Conjunto&); // Operador copia

   private:
...
    void PreOrdenCopia(pElemento elemento);
...

Conjunto::Conjunto(const Conjunto& A) : raiz(nullptr) {
    Vaciar();
    PreOrdenCopia(A.raiz);
}

void Conjunto::PreOrdenCopia(pElemento elemento) {
    if(elemento) {
        Insertar(elemento->valor);
        PreOrdenCopia(elemento->izquierdo);
        PreOrdenCopia(elemento->derecho);
    }
}

13.4.2 Operador de asignación

Por el mismo motivo que hemos definido el constructor copia, sobrecargaremos el operador de asignación.

Disponiendo del constructor copia, la implementación es trivial:

Conjunto Conjunto::operator=(const Conjunto& B) {
    if(*this != B) {
        Vaciar();
        PreOrdenCopia(B.raiz);
    }
    return *this;
}

13.4.3 Operador suma, unión

Conservaremos las dos formas, un método Union y su equivalente usando el operador +.

También usaremos un método privado auxiliar, PreOrdenUnión:

class Conjunto {
   public:
...
    Conjunto Union(const Conjunto& B) const;
    Conjunto operator+(const Conjunto& B);
...
   private:
...
    void PreOrdenUnion(pElemento n);
...

Conjunto Conjunto::Union(const Conjunto& B) const{
    Conjunto U;

    U.PreOrdenUnion(this->raiz);
    U.PreOrdenUnion(B.raiz);
    return U;
}

Conjunto Conjunto::operator+(const Conjunto& B) {
    return Conjunto(Union(B));
}

void Conjunto::PreOrdenUnion(pElemento n) {
    if(n) {
        Insertar(n->valor);
        PreOrdenUnion(n->izquierdo);
        PreOrdenUnion(n->derecho);
    }
}

13.4.4 Operador de intersección

EL mismo mecanismo se puede utilizar para el resto de operaciones.

Para la intersección tenemos:

class Conjunto {
   public:
...
    Conjunto Interseccion(const Conjunto& B) const;
    Conjunto operator&(const Conjunto& B) const;
...
   private:
...
    void PreOrdenIntereseccion(pElemento n, const Conjunto& B);
...

Conjunto Conjunto::Interseccion(const Conjunto& B) const {
    Conjunto U;

    U.PreOrdenIntereseccion(this->raiz, B);
    return U;
}

Conjunto Conjunto::operator&(const Conjunto& B)  const {
    return Conjunto(Interseccion(B));
}

void Conjunto::PreOrdenIntereseccion(pElemento n, const Conjunto& B) {
    if(n) {
        if(B.Pertenece(n->valor)) Insertar(n->valor);
        PreOrdenIntereseccion(n->izquierdo, B);
        PreOrdenIntereseccion(n->derecho, B);
    }
}

13.4.5 Operadores de diferencia y diferencia simétrica

El mecanismo es muy parecido para estas dos operaciones;

class Conjunto {
   public:
...
    Conjunto Diferencia(const Conjunto& B) const;
    Conjunto operator-(const Conjunto& B) const;
    Conjunto DiferenciaSimétrica(const Conjunto& B) const;
    Conjunto operator^(const Conjunto& B) const;
...
   private:
...
    void PreOrdenDiferencia(pElemento n, const Conjunto& B);
...
Conjunto Conjunto::Diferencia(const Conjunto& B) const {
    Conjunto D;

    D.PreOrdenDiferencia(this->raiz, B);
    return D;
}

Conjunto Conjunto::operator-(const Conjunto& B) const {
    return Conjunto(Diferencia(B));
}

Conjunto Conjunto::DiferenciaSimetrica(const Conjunto& B) const {
    Conjunto S;

    S.PreOrdenDiferencia(this->raiz, B);
    S.PreOrdenDiferencia(B.raiz, *this);
    return S;
}

Conjunto Conjunto::operator^(const Conjunto& B) const {
    return Conjunto(DiferenciaSimetrica(B));
}

void Conjunto::PreOrdenDiferencia(pElemento n, const Conjunto& B) {
    if(n) {
        if(!B.Pertenece(n->valor)) Insertar(n->valor);
        PreOrdenDiferencia(n->izquierdo, B);
        PreOrdenDiferencia(n->derecho, B);
    }
}

13.4.6 Operadores de igualdad y desigualdad

Nos puede interesar comparar conjuntos, y para ello sobrecargaremos los operadores de igualdad y desigualdad:

class Conjunto {
   public:
...
    bool operator==(const Conjunto& B) const;
    bool operator!=(const Conjunto& B) const;
   private:
...
    void PreOrdenIgualdad(bool* retval,  pElemento n, const Conjunto& B);
...

bool Conjunto::operator==(const Conjunto& B) const {
    bool retval=true;
    if(Cardinalidad() != B.Cardinalidad()) return false;
    else PreOrdenIgualdad(&retval, raiz, B);
    return retval;
}

bool Conjunto::operator!=(const Conjunto& B) const {
    return !(*this==B);
}

void Conjunto::PreOrdenIgualdad(bool* retval, pElemento n, const Conjunto& B) {
    if(!*retval) return;
    if(n && B.Pertenece(n->valor)) {
        PreOrdenIgualdad(retval,n->izquierdo, B);
        PreOrdenIgualdad(retval, n->derecho, B);
    } else *retval &= false;
}

13.4.7 Métodos de subconjunto y superconjunto

Finalmente, para las operaciones de subconjunto y superconjunto sólo definiremos los métodos:

bool Conjunto::Subconjunto(const Conjunto& B) const {
    bool retval=true;
    if(Cardinalidad() > B.Cardinalidad()) return false;
    else PreOrdenIgualdad(&retval, raiz, B);
    return retval;
}

bool Conjunto::Superconjunto(const Conjunto& B) const {
    return B.Subconjunto(*this);
}

13.5 Constructor a partir de lista inicializadora

En este tipo de estructuras puede ser interesante crear un constructor que nos permita crear el conjunto con una lista de valores iniciales. C++11 permite usar este tipo de inicializaciones:

    Conjunto K = {10, 20, 30, 40};

Esto nos ahorraría escribir código, añadir otro constructor sólo se hace una vez, crear conjuntos probablemente se haga más veces. También ayuda a crear un código más claro.

El código para un constructor de este tipo tiene esta forma:

class Conjunto {
   public:
...
    Conjunto(std::initializer_list<int>);
...
Conjunto::Conjunto(std::initializer_list<int> a) : raiz(nullptr) {
    for(int v:a) Insertar(v);
}

13.6 Constructor y operador de asignación de movimiento

C++11 también permite usar semántica de movimiento.

Imaginemos que tenemos dos conjuntos de objetos de un tamaño importante y muchos elementos, y tenemos que calcular su unión.

Nuestro código para calcular la unión crea un objeto local, le añade los elementos de los dos conjuntos de entrada, y devuelve ese objeto local.

Conjunto Conjunto::Union(const Conjunto& B) const{
    Conjunto U;

    U.PreOrdenUnion(this->raiz);
    U.PreOrdenUnion(B.raiz);
    return U;
}
...
    Conjunto U(A.Union(B)); // Equivale a: U =  A+B;

Cuando calculamos el conjunto U primero se invoca a nuestro método Union, que crea y devuelve un objeto temporal, que en principio tendrá muchos elementos y ocupará mucha memoria. Después usa el operador copia para copiar ese objeto al conjunto U, y finalmente destruye el objeto temporal.

Es evidente que estamos usando recursos de una forma poco eficiente, y sería interesante poder ahorrarnos una copia y destrucción, tanto en tiempo de ejecución como en consumo de memoria.

Ahí es donde entra la semántica de movimiento. Este mecanismo nos permite mover el objeto temporal al objeto de destino sin necesidad de copiarlo y destruirlo.

Lo mismo se aplica al operador de asignación, usando un operador de asignación de movimiento.

El constructor de movimiento tiene esta forma:

class Conjunto {
   public:
...
    Conjunto(Conjunto&& A); // Constructor de movimiento
...
Conjunto::Conjunto(Conjunto&& A) {
    raiz = A.raiz;
    A.raiz = nullptr;
}

Y el operador de asignación de movimiento esta:

class Conjunto {
   public:
...
    Conjunto&: operator=(Conjunto&& B);
...
Conjunto& Conjunto::operator=(Conjunto&& B) {
    if(*this != B) {
        Vaciar();
        raiz = B.raiz;
        B.raiz = nullptr;
    }
    return *this;
}

No tiene sentido mover un objeto a si mismo. En ese caso simplemente devolvemos el objeto.

Si el conjunto que va a recibir la copia ya tenía elementos, los eliminaremos y copiamos el puntero al nodo raíz. Posteriormente anulamos el nodo raíz del objeto movido para evitar que el destructor libere la memoria que ahora pertenece al objeto copia.

Para usar este mecanismo en nuestro programa tendremos que usar expresiones diferentes.

Por ejemplo:

    Conjunto K({10, 20, 30, 40});
    Conjunto H;
    H = std::move(K); // 1
    Conjunto L(std::move(H));  // 2

En 1 se usa el operador de asignación de movimiento. El conjunto H será una copia de K, y K quedará vacío después de la asignación.

En 2 se usa el constructor de movimiento. El conjunto L será una copia de H, y H quedará vacío después de la asignación.

Evidentemente, la sintaxis no es tan limpia como para el operador de asignación y el constructor copia, pero cuando se usan correctamente mejoran notablemente el programa.

Una forma mas eficiente de calcular la unión de dos conjuntos, usando semántica de movimiento es:

    U = std::move(A + B);

13.7 Utilidad de los conjuntos

Los conjuntos se pueden utilizar en la resolución de multitud de problemas.

12.8 Fichero con el código fuente

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Ejemplo de conjunto en C	conjuntoc.zip	2025-11-06	2936 bytes	4

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Ejemplo de conjunto en C++	conjuntocpp.zip	2025-11-06	3702 bytes	4

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Ejemplo de conjunto en C++ con plantillas	conjuntotemplate.zip	2025-11-06	4416 bytes	5

Nota: para la versión con plantillas ha sido necesario modificar la clase Cadena para añadir un constructor a partir de una cadena C constante:

class Cadena {
  public:
...
   Cadena(const char *cad) {
      cadena = new char[strlen(cad)+1];
      strcpy(cadena, cad);
   }
...

Esto evita que el compilador emita un warning cada vez que intentamos añadir al conjunto una cadena literal.