11 Árboles rojo-negro

Seguimos con más estructuras de datos de tipo árbol.

Le toca el turno a los árboles rojo-negro, a partir de ahrra árboles RN, que como veremos más adelante, se usan para implementar otros tipos de estructuras de datos.

11.1 Qué son

Los árboles RN son árboles binarios de búsqueda casi-balanceados. Se parecen bastante a los árboles AVL, pero tienen algunas diferencias que los hacen más útiles en determinadas circunstancias.

Cada nodo tiene asignado un color: rojo o negro. Estos colores se usan para mantener el árbol equilibrado. Existen ciertas reglas para asignar el color de cada nodo:

• El nodo raíz siempre es de color negro.
• No puede haber dos nodos adyacentes de color rojo.
• Cada ruta del árbol (desde el nodo raíz hasta el nodo hoja) debe tener la misma cantidad de nodos de color negro.

Al aplicar estas reglas resulta que el camino más largo desde la raíz hasta una hoja no es más largo que el doble del camino más corto desde la raíz a una hoja.

Los árboles RN no están siempre perfectamente equilibrados, pero se aproximan bastante.

Veremos que las operaciones de equilibrado son parecidas a las de los árboles AVL, pero en este tipo de árboles son más eficientes.

Como resultado tienen un buen peor caso de tiempo de ejecución para sus operaciones de búsqueda, inserción y borrado. Y permiten buscar, insertar y borrar en un tiempo O(log n).

11.2 Operaciones

Tendremos las operaciones habituales en árboles de búsqueda:

• Buscar un elemento.
• Insertar un elemento.
• Borrar un elemento.
• Movimientos a través del árbol:
  • Izquierda.
  • Derecha.
  • Raiz.
  • Asignar color.
  • Equilibrar después de insertar.
  • Equilibrar después de borrar.
• Información:
  • Comprobar si un árbol está vacío.
  • Obtener color de un nodo.

Aunque es posible crear árboles RN con valores repetidos, en este caso no lo haremos. Si se intenta insertar un nodo que ya existe, sencillamente no lo insertaremos. En la variante con nodos repetidos, para la rama derecha se establece la comparación mayor o igual, en lugar de mayor.

En otras estructuras de datos, como los conjuntos que veremos más adelante. se usan estos árboles, pero no se admiten valores repetidos.

11.3 Búsqueda

Las operaciones de búsqueda son similares a las de los árboles binarios de búsqueda

Partiendo siempre del nodo raíz, el modo de buscar un elemento se define de forma recursiva.

• Si el árbol está vacío, terminamos la búsqueda: el elemento no está en el árbol.
• Si el valor del nodo raíz es igual que el del elemento que buscamos, terminamos la búsqueda con éxito.
• Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo.
• Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho.
• El valor de retorno de una función de búsqueda puede ser un puntero al nodo encontrado, o NULL, si no se ha encontrado.

11.4 Rotaciones

Como en el caso de los árboles AVL, en estas estructuras también tendremos que hacer rotaciones para que los árboles mantengan las reglas después de añadir o eliminar un nodo.

Existen cuatro posibles rotaciones dos simples: rotación a la derecha o a la izquierda, y dos dobles: rotación izquierda-derecha y rotación derecha-izquierda.

Hay que tener siempre presente que las relaciones entre nodos son dobles, es decir, un nodo tiene un puntero que señala a su hijo izquierdo, pero ese hijo tiene un puntero que señala a su nodo padre. Cambiar uno de esos punteros implica que debemos cambiar el otro para mantener la estructura consistente.

11.4.1 Rotación a la derecha

Las rotaciones simples implican dos nodos: Q y P, siendo P el nodo padre de Q. Como norma general, asumiremos que Q tendrá dos subárboles izquierdo y derecho (A y B), P tendrá un subárbol derecho (C), y existirá un nodo superior cuya rama derecha o izquierda sea P, salvo que P sea el nodo raíz.

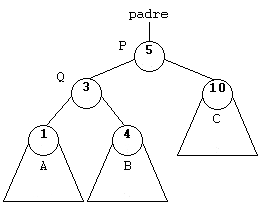
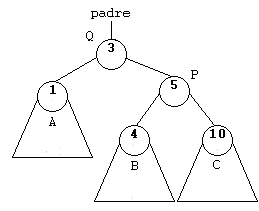
En cualquier operación de rotación es importante mantener cierto orden de modo que no se pierdan valores de punteros que hagan imposible acceder a ciertos nodos.

Esta rotación será necesaria cuando el número de nodos negros en el subárbol C sea menor que en la rama Q. Q debe ser Negro.

El proceso es similar al que vimos en el capítulo de los árboles AVL, y el siguiente:

1. Guardamos un puntero al nodo Q y otro al nodo P.
2. Haremos que el subárbol izquierdo de P sea el subárbol derecho de Q: P->izquierdo=Q->derecho. (Q->izquierdo->padre=P).
3. El subárbol derecho de Q será el subárbol con en nodo raíz P. Q->derecho=P. (P->padre=Q).
4. A continuación hay tres posibilidades:
   • El padre de P, P->padre es NULL, es decir, P era el nodo raíz del árbol. En ese caso haremos que Q pase a ser el nodo raíz. Q->padre=NULL, y raiz=Q.
   • P sea el nodo izquierdo del nodo padre de P. P-padre->izquierdo==P. Haremos que esa rama ahora apunte al nodo Q: P-padre->izquierdo=Q. (Q->padre=P->padre).
   • P sea el nodo derecho del nodo padre de P. P-padre->derecho==P. Haremos que esa rama ahora apunte al nodo Q: P-padre->derecho=Q. (Q->padre=P->padre).

11.4.2 Rotación a la izquierda

La situación es análoga, ahora tenemos de nuevo dos nodos: Q y P. Asumiremos que P tendrá dos subárboles izquierdo y derecho (A y B), Q tendrá un subárbol izquierdo (C), y existirá un nodo superior cuya rama derecha o izquierda sea P, salvo que P sea el nodo raíz.

Esta rotación será necesaria cuando el número de nodos negros en el subárbol A sea menor que en la rama Q. Q debe ser Negro.

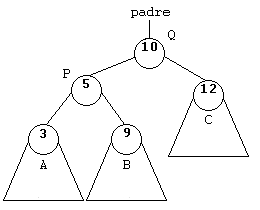
El proceso es el siguiente:

1. Guardamos un puntero al nodo Q y otro al nodo P.
2. Haremos que el subárbol derecho de P sea el subárbol izquierdo de Q: P->derecho=Q->izquierdo. (Q->derecho->padre=P).
3. El subárbol izquierdo de Q será el subárbol con en nodo raíz P. Q->izquierdo=P. (P->padre=Q).
4. A continuación hay tres posibilidades:
   • El padre de P, P->padre es NULL, es decir, P era el nodo raíz del árbol. En ese caso haremos que Q pase a ser el nodo raíz. Q->padre=NULL, y raiz=Q.
   • P sea el nodo izquierdo del nodo padre de P. P-padre->izquierdo==P. Haremos que esa rama ahora apunte al nodo Q: P-padre->izquierdo=Q. (Q->padre=P->padre).
   • P sea el nodo derecho del nodo padre de P. P-padre->derecho==P. Haremos que esa rama ahora apunte al nodo Q: P-padre->derecho=Q. (Q->padre=P->padre).

11.4.3 Rotaciones dobles

Aunque se pueden aplicar rotaciones dobles sobre árboles RN, en la práctica, los algoritmos que aplicaremos para equilibrar estas estructuras no requieren este tipo de rotaciones, de modo que no las comentaremos.

11.4 Inserción

El proceso de inserción también es igual que en los árboles binarios de búsqueda.

Siempre que se inserta un nodo, se le asignará el color rojo, y siempre se insertará en un nodo hoja. Como resultado puede suceder que el árbol contenga dos nodos rojos consecutivos, lo cual contradice las reglas.

Por lo tanto, después de cada inserción deberemos aplicar un procedimiento para corregir cualquier estado no válido.

El procedimiento es el siguiente.

• Tenemos un árbol RN, cuyo nodo raíz es R, que puede ser NULL si el árbol está vacío.
• Creamos un nuevo nodo N, asignándole el valor a insertar, el color rojo y cuyos nodos izquierdo y derecho son NULL.
• Si el árbol está vacío, R==NULL, entonces haremos que en nodo N sea el raíz, y cambiaremos su color a negro.
• En caso contrario, empezando en el nodo raíz, usaremos un nodo auxiliar A, y repetiremos hasta llegar a un nodo hoja con el valor a insertar o hasta que A sea NULL.
  • Guardamos el nodo A. B=A.
  • Si el valor del nodo A es menor que el del nodo N, continuaremos por el árbol izquierdo: A = A->izquierdo.
  • Si el valor del nodo A es mayor que el del nodo N, continuaremos por el árbol derecho: A = A->derecho.
• Si el valor del nodo B es el valor a insertar, regresaremos sin hacer nada.
• Si el valor del nodo B es menor que el del nodo N, insertaremos N en la rama izquierda de B: B->izquierdo=N.
• Si el valor del nodo B es mayor que el del nodo N, insertaremos N en la rama derecha de B: B->derecho=N.
• Reequilibrar el árbol, si es necesario.

11.5 Reequilibrado después de la inserción

Reequilibrar un árbol RN después de una inserción es relativamente sencillo, gracias a la propiedad de color de cada nodo.

Existen seis posibles casos, que podemos resumir en tres, si tenemos en cuenta la simetría derecha-izquierda.

Siempre partimos del nodo insertado, que tendrá color Rojo, y verificaremos si su nodo padre también es Rojo, en cuyo caso estaremos ante un árbol RN no válido.

Como resultado de cualquier corrección, el árbol RN puede que haya quedado en un estado válido o no. En cualquier caso deberemos seguir verificando y corrigiendo su estado.

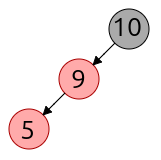
11.5.1 Primer caso

Hemos insertado el nodo N, cuyo nodo padre es P, y el nodo padre de P es Q. El nodo N está en la rama derecha de P.

Tanto P como N son Rojos.

Verificamos que P es el nodo izquierdo de Q, y además Q no tiene un nodo derecho. En ese caso tendremos que hacer una rotación izquierda de P.

El resultado sigue sin cumplir las reglas, por lo que seguiremos iterando, pero ahora el nodo N pasa a ser el nodo P, N=P.

11.5.2 Segundo caso

El segundo caso es que hayamos añadido el nodo N, o que vengamos del caso anterior.

Lo primero que tenemos que verificar es que en nodo N y su nodo padre P son ambos Rojos. Esto contradice la definición de un árbol RN.

Ahora P es el nodo izquierdo de Q, y Q no tiene un nodo derecho.

En ese caso tendremos que hacer una rotación derecha de P.

Además, cambiaremos el color del nodo P a Negro y el del nodo Q a Rojo.

11.5.3 Tercer caso

En el tercer y último caso nos encontramos con el nodo N recién añadido, que será Rojo, su nodo padre P, y el nodo padre de P, Q.

Lo primero que tenemos que verificar es que en nuevo nodo N y su nodo padre P son ambos Rojos. Esto contradice la definición de un árbol RN.

Además, P es el nodo izquierdo de Q, y Q posee un nodo derecho no nulo.

En ese caso no tendremos que hacer ninguna rotación, bastará con asignar el color Negro a los dos nodos hijos de Q, y el color Rojo al nodo Q.

En cualquiera de los tres casos, el número de nodos negros de la rama no cambia, y hemos eliminado los nodos rojos consecutivos. Por lo tanto el árbol sigue siendo válido.

En el caso particular, como sucede en este ejemplo, de que Q sea el nodo raíz, y como resultado de aplicar este caso termine siendo Rojo, tendríamos que cambiar su color a Negro, ya que el nodo raíz de un árbol RN debe ser Negro, y nada impide que haya dos nodos negros consecutivos.

11.5.4 Algoritmo

Tomaremos como valor de entrada el nuevo nodo insertado N.

• Repetiremos el bucle mientras el nodo N no sea el raíz, y el nodo padre de N sea Rojo.
  • Usaremos dos nodos auxiliares: P, que es el nodo padre de N, y Q que es el nodo padre de P. (Ambos nodos existen, P porque es la primera condición del bucle y Q porque P debe ser Rojo, y sabemos que el nodo raíz siempre es Negro.
  • Si P es el nodo izquierdo de Q:
    1. Si no existe un Q->derecho y N es el nodo derecho de P: haremos una rotación a la izquierda de P y N=P.
    2. Si no existe un Q->derecho y N es el nodo izquierdo de P: cambiamos el color de Q a Rojo, el de P a Negro, y haremos una rotación a la derecha de P.
    3. Si existe Q->derecho y es Rojo: cambiamos el color de W->derecho y Q->izquierdo a Negro y el de Q a Rojo. Y hacemos que N=Q.
  • Si P es el nodo derecho de Q:
    1. Si no existe Q->izquierdo, y N es el nodo izquierdo de P: haremos una rotación a la derecha de P y N=P.
    2. Si no existe Q->izquierdo, y N es el nodo derecho de P: cambiamos el color de Q a Rojo, el de P a Negro, y hacemos una rotación a la izquierda de P.
    3. Si existe Q->izquierdo y es Rojo: cambiamos el color de Q->derecho y Q->izquierdo a Negro y el de Q a Rojo. Y hacemos que N=Q.
• Finalmente, siempre cambiamos el color del nodo raíz a Negro.

11.6 Borrado de nodos

El método para el borrado de nodos es similar al de árboles ABB o AVL.

Para borrar un elemento también nos basamos en el algoritmo de búsqueda. Si el elemento no está en el árbol no lo podremos borrar. Si está, hay dos casos posibles:

• O bien se trata de un nodo hoja, en cuyo caso lo borraremos directamente.
• O bien se trata de un nodo rama: en ese caso no podemos eliminarlo sin más, ya que perderíamos el acceso a sus subárboles hijos. En su lugar buscamos el nodo más a la izquierda de su subárbol derecho, o el más a la derecha del subárbol izquierdo e intercambiamos sus valores. Para finalizar eliminando el nodo hoja intercambiado.

Como siempre eliminaremos un nodo hoja, estaremos en una situación simétrica a la que teníamos al insertar un nodo.

Si el nodo a eliminar tiene color Rojo, no hay problema. Es lo mismo que borrar un nodo recién añadido, que siempre será Rojo. Como resultado, el número de nodos negros en todas las rutas desde la raíz a cada nodo hoja será el mismo.

Los problemas surgen al borrar un nodo Negro, ya que esto cambiará el número de nodos negros en ciertas rutas.

La rama a la que pertenece el nodo objetivo tendrá un nodo Negro menos, de modo que nuestro objetivo es añadir un nodo negro a esa rama, o eliminarlo del resto.

Veremos que dependiendo del color de su nodo hermano, y del color de los nodos hijos de éste, tendremos que realizar diferentes tareas para recuperar el estado del árbol RN.

Hay que tener en cuenta que, análogamente a lo que ocurría al insertar nodos, a veces será necesario repetir el proceso de reequilibrado, ya que un primer intento puede que no resulte en un árbol RN válido. Por lo tanto, no siempre el nodo objetivo será el nodo eliminado.

La mayoría de la documentación sobre este tipo de estructuras usan el concepto de "doble negro" para resolver estas situaciones.

Pensemos qué sucede cuando se elimina un nodo Negro. Ese nodo ya tenía dos nodos nulos que por definición son de color Negro, por lo tanto, en la rama que empieza en ese nodo había dos nodos de color Negro. Cuando ese nodo se elimina, en su lugar queda un único nodo nulo, de modo que esa rama ahora sólo tiene un nodo Negro. Ahí entra el concepto de "doble negro". El nodo nulo adquiere la propiedad de color del nodo eliminado, de modo que ahora es doblemente Negro.

El objetivo ahora es eliminar ese "doble negro". Mediante rotaciones intentaremos transferir el Negro extra al nodo padre. Cuando el nodo padre en Negro, ese nodo adquiere la propiedad de "doble negro", pero cuando es rojo pasa a ser Negro, y el árbol queda equilibrado.

Otra forma de verlo es que el objetivo sea convertir el nodo "doble negro" a Rojo.

Se pueden dar varias situaciones diferentes:

11.6.1 Primer caso

En la imagen se muestra una estructura de una rama de un árbol RN equilibrado, todas las ramas tienen el mismo número de nodos de color Negro.

En este caso el nodo a eliminar es el nodo hoja A.

Si eliminamos el nodo A, en su lugar queda un nodo nulo "doble negro". Nuestro primer objetivo es que el nodo A tenga un hermano de color Negro.

Por lo tanto, el primer caso se da cuando el nodo hermano del "doble negro" es Rojo. El procedimiento en este caso no resuelve el equilibrio, el objetivo es pasar a un estado donde poder aplicar el segundo caso.

De momento dejemos el primer caso para después.

11.6.2 Segundo caso

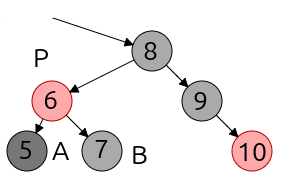
Ahora el nodo "doble negro" también es el nodo hoja A. Esto puede suceder porque haya que borrar el nodo A, o porque se ha borrado un nodo en esa rama, y el proceso de equilibrado haya transferido la propiedad de "doble negro" a ese nodo.

En este caso, el nodo hermano de A, B es Negro. Además, los dos nodos hijos de B son negros, recordemos que todos los nodos nulos se consideran negros.

Para restablecer el equilibrio hay que:

• Cambiar el color del nodo "doble negro", A, y del nodo hermano, B, a Rojo.
• El nodo "doble negro" transfiere su propiedad a su nodo padre.
• Si el nodo padre era Rojo pasa a ser negro, y el árbol queda equilibrado.
• Si el nodo padre era previamente Negro ahora es "doble negro", por lo que repetiremos el proceso, usando como nodo "doble negro" el nodo padre.

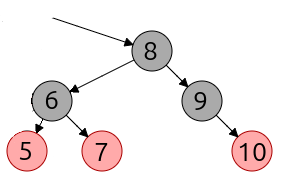
En el caso general, cuando el nodo A no sea el nodo a borrar, el mecanismo es el mismo.

Volvamos ahora al primer caso.

Nuestro objetivo ahora no es equilibrar el árbol, sino deshacernos del nodo hermano Rojo. Eso pasará de este primer caso al segundo, tercero o cuarto, dependiendo del color de los hijos del nodo hermano. Para ello bastará con rotar el nodo B a la izquierda, y cambiar los colores de los nodos B y P.

El procedimiento consiste en:

• Cambiar el color del nodo hermano, B, a Negro.
• Cambiar el del nodo padre, P a Rojo.
• Rotamos a la izquierda el nodo hermano.

• Ahora, el nodo A sigue siendo "doble negro", seguimos aplicando el algoritmo de nuevo pero ahora estaremos ante un caso 2, 3 ó 4.

11.6.3 Tercer caso

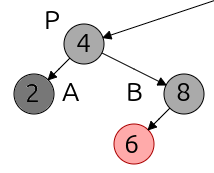
Como sucede con el caso 1, en este caso el objetivo no es equilibrar el árbol, sino pasar al caso 4.

El caso 3 se da cuando el nodo hermano del "doble negro" es negro, y su hijo más cercano al "doble negro" es Rojo.

Es decir, si el nodo "doble negro" es un nodo izquierdo, y el nodo izquierdo del nodo hermano es Rojo y el derecho Negro, o si el nodo "doble negro" es un nodo derecho y el nodo derecho del hermano es Rojo y el izquierdo Negro.

El caso 4 es cuando el hermano de "doble negro" es negro y su hijo más lejano al "doble negro" es Rojo. Para llegar a esa situación el procedimiento es:

• Intercambiar los colores del nodo hermano con el de su nodo hijo Rojo. Es decir, el nodo hermano pasa a ser Rojo, y su hijo Negro.
• Rotamos el nodo hermano en la dirección opuesta al "doble negro" (si el nodo objetivo es un hijo derecho, aplique rotaciones a la izquierda y viceversa).
• Ahora, manteniendo el mismo nodo como "doble negro", estaremos ante un caso 4.

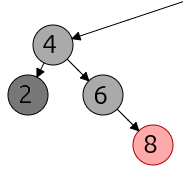
Como en los casos anteriores, en el caso general el nodo A no tiene por qué ser un nodo hoja a borrar, podemos haber llegado a este caso como consecuencia de aplicar otro caso previamente en una de las ramas de A. pero el mecanismo es el mismo.

11.6.4 Cuarto caso

Si el hermano del nodo "doble negro" es un nodo Negro, pero el nodo hijo del hermano que está más lejos del objetivo es Rojo.

El color del otro nodo hijo del nodo hermano no importa.

• Asignamos a nodo hermano, B, el color de su nodo padre, P.
• El nodo padre, P, pasa a ser Negro.
• Al nodo hijo del hermano más alejado del nodo objetivo le asignamos el color Negro.
• Rotamos el hermano, B, en la dirección del nodo "doble negro" (es decir, si es un hijo derecho, aplique rotaciones a la derecha y viceversa).
• El árbol queda equilibrado, podemos abandonar el proceso.

En general, la rama A tenía originalmente un nodo Negro menos que la B. Después de aplicar el método anterior, A está a un nivel más bajo, y tiene un nodo Negro más en su ruta hacia la raíz. En este caso, el nodo 8 ahora es el padre de 4.

El nodo 4 está equilibrado, así como su nodo padre, el 8.

11.7 Ejemplo de árbol RN en C

Para almacenar los colores usaremos un enumerado:

typedef enum {
    Negro=0,
    Rojo
} tipoColor;

Cada nodo necesita almacenar el valor, el color, un puntero a cada rama y otro al nodo padre:

typedef struct _nodo {
    int valor;
    tipoColor color;
    struct _nodo* padre;
    struct _nodo* izquierdo;
    struct _nodo* derecho;
} tipoNodo;

También será útil definir otros dos tipos, uno para declarar variables de tipo puntero a nodo, el otro, aunque sea equivalente, para declarar el árbol:

typedef tipoNodo *pNodo;
typedef tipoNodo *Arbol;

La mayor parte de los procedimientos son bastante triviales. Los más interesantes son las rotaciones y los procedimientos de inserción, borrado y equilibrado.

Por ejemplo, la rotación a la derecha:

void RotacionDerecha(Arbol *arbol, pNodo A) {
    pNodo B = A->padre;
    B->izquierdo = A->derecho;
    if(B->izquierdo) B->izquierdo->padre = B;
    if(!B->padre) {
        A->padre = NULL;
        *arbol = A;
    } else
    if(B == B->padre->izquierdo) {
        B->padre->izquierdo=A;
        A->padre = B->padre;
    } else {
        B->padre->derecho=A;
        A->padre = B->padre;
    }
    A->derecho = B;
    B->padre = A;
}

El procedimiento para insertar un nodo:

void Insertar(Arbol *arbol, int v) {
    pNodo a = *arbol;
    pNodo b = a;
    pNodo nuevo;

    if(*arbol==NULL) { // Árbol vacío
        *arbol = (pNodo)malloc(sizeof(tipoNodo));
        (*arbol)->valor = v;
        (*arbol)->color = Negro;
        (*arbol)->padre = (*arbol)->izquierdo = (*arbol)->derecho = NULL;
        return;
    }

    while(a && v != a->valor) {
        b = a;
        if(v < a->valor) a = a->izquierdo;
        else if(v > a->valor) a = a->derecho;
    }

    if(v == b->valor) return; /* El árbol ya contiene el valor */

    nuevo = (pNodo)malloc(sizeof(tipoNodo));
    nuevo->valor = v;
    nuevo->color = Rojo;
    nuevo->izquierdo = nuevo->derecho = NULL;

    if(v < b->valor) {
        b->izquierdo = nuevo;
    } else {
        b->derecho = nuevo;
    }
    nuevo->padre = b;
    EquilibrarInsercion(arbol, nuevo);
}

O el de equilibrar después de insertar:

void EquilibrarInsercion(Arbol *a, pNodo n) {
    pNodo p, pp;

    while(n->padre && n->padre->color==Rojo) {
        p = n->padre;
        pp = p->padre;
        if(p == pp->izquierdo) {
            if(pp->derecho && pp->derecho->color==Rojo) {
                pp->derecho->color = Negro;
                pp->izquierdo->color = Negro;
                pp->color = Rojo;
                n = pp;
            } else
            if(n == p->derecho) {
                n = p;
                RotacionIzquierda(a, p);
            } else {
                p->color = Negro;
                pp->color = Rojo;
                RotacionDerecha(a, p);
            }
        } else {
            if(pp->izquierdo && pp->izquierdo->color == Rojo) {
                pp->derecho->color = Negro;
                pp->izquierdo->color = Negro;
                pp->color = Rojo;
                n = pp;
            } else
            if(n == p->izquierdo) {
                RotacionDerecha(a, n);
                n = p;
            } else {
                p->color = Negro;
                pp->color = Rojo;
                RotacionIzquierda(a, p);
            }
        }
    }
    (*a)->color = Negro;
}

11.8 Ejemplo de árbol RN en C++

Usando clases el código es muy parecido, tan sólo hay que encapsular el código C en las clases correspondientes.

11.9 Ejemplo de árbol RN en C++ con plantillas

El código usando plantillas es una simple generalización del anterior.

11.10 Fichero con el código fuente

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Árbol RN en C	arbolrn_c.c.zip	2025-10-27	2201 bytes	4

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Árbol RN en C++	arbolrn_cpp.cpp.zip	2025-10-27	2294 bytes	4

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Árbol RN en C++ con plantillas	arbolrn_templ.cpp.zip	2025-10-27	3146 bytes	4

11.11 Bibliografía

Visualización de árboles RN.

programiz.com red-black-tree.

Veamos un caso más general.

Pero en general, el nodo A no tiene por qué ser el nodo a eliminar. Podríamos haber llegado a este punto al equilibrar las ramas izquierda y derecha del nodo A. Es decir, el árbol con raíz en A cumpliría las reglas de los árboles RN, pero el que tiene por raíz su padre, P, estaría desequilibrado, teniendo la rama A un nodo Negro menos que la B.

Aplicando este caso hemos eliminado un nodo negro de la rama B, equilibrando el árbol con raíz P, pero si P tiene un nodo padre, la otra rama tendrá de nuevo un nodo Negro más.

Por ejemplo, si en éste árbol eliminamos el nodo 1, estaremos ante un caso 1. El nodo 3 pasa a Rojo, y subimos un nivel.

Usando el nodo 2 como objetivo, volvemos a estar ante un caso 1. El nodo 8 pasa a Rojo, y subimos un nivel.

Como el nodo 4 es Rojo lo cambiamos a Negro, esto añade un nodo Negro a la rama y el árbol queda equilibrado.