8 Colisiones

En la mayor parte de los juegos tendremos que detectar colisiones entre objetos, ya sea para simular la física de rebotes, o para detectar el impacto de disparos, choques, etc.

En los juegos se usan cajas de colisión, o hitboxes, para detectar colisiones. Un hitbox es un área simplificada, no visible en el juego, que sustituye al objeto cuando se busca detectar colisiones. En juegos 2D suelen ser rectángulos, círculos o elipses. Siempre es más sencillo calcular intersecciones entre figuras simples que entre formas complejas, y en la dinámica del juego, si los hitboxes están bien calculados, la diferencia es inapreciable.

Como norma general, los hitboxes, tanto si son rectángulos como elipses, tienen sus ejes de simetría paralelos a los ejes cartesianos, es decir, no se usan rectángulos o elipses rotados, ya que en esos casos los cálculos no son triviales, y no sería posible calcular colisiones en tiempo real.

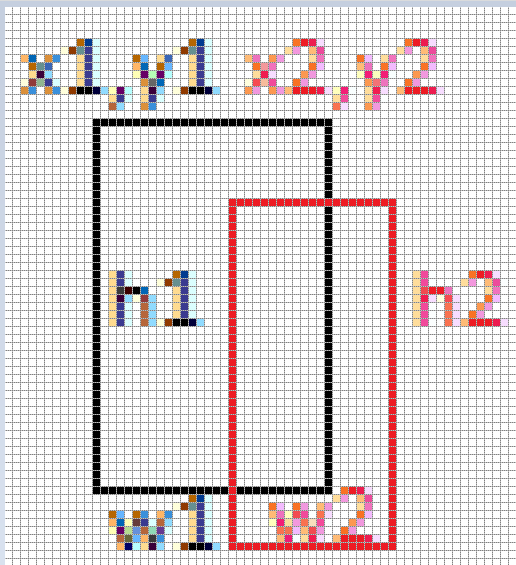
Calcular colisiones entre rectángulos es simple. Siendo (x1,y1,w1,h1) y (x2,y2,w2,h2) las coordenadas de los dos rectángulo, el rectángulo intersección tendrá las coordenadas (xi,yi) = (max(x1,x2),max(y1,y2)), la anchura será min(x1+w1,x2+w2)-xi, y la altura min(y1+h1,y2+h2)-yi. Si la anchura o la altura fuesen negativas, no hay intersección.

Por ejemplo, si tenemos los rectángulos R1=(10,20,10,15) y R2=(15,10,10,15):

xi = max(10,15) = 15
yi = max(20,10) = 20
wi = min(10+10,15+10)-15 = min(20,25)-15 = 5
hi = min(20+15,10+15)-20 = min(35,25)-20 = 5
Ri = (15,20,5,5)

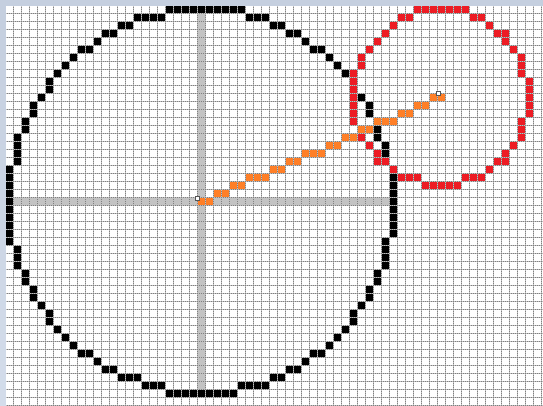
Verificar si dos círculos se intersecan, también es simple. Si la distancia entre sus centros es menor que la suma de sus radios, hay intersección.

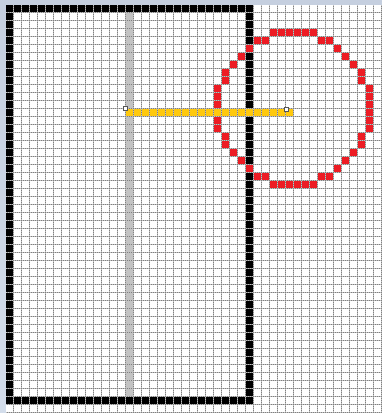
También es sencillo verificar si existe intersección entre un rectángulo y un círculo.

Es importante elegir correctamente los hitboxes. La forma a elegir dependerá del tipo de objeto, algunos objetos funcionarán muy buen con hitboxes rectangulares y otros lo harán mejor con círculos.

A la hora de calcular el hitbox de un objeto podemos optar por dos caminos:

• Elegir un hitbox que se adapte aceptablemente en cualquier situación del juego.
• Recalcular el hitbox cada vez que el objeto cambie de orientación.

Para objetos que no vayan a rotar, o que aunque lo hagan el hitbox no se vea muy afectado se puede usar la primera opción. A veces es mejor elegir un hitbox que deje fuera parte del objeto (caso B), en lugar de elegir uno que contenga todo el objeto (caso A). Depende de si la prioridad es evitar falsas colisiones o evitar colisiones que no se han producido.

Si los objetos cambian de orientación, es mejor usar la segunda opción, y recalcular la hitbox cada vez.

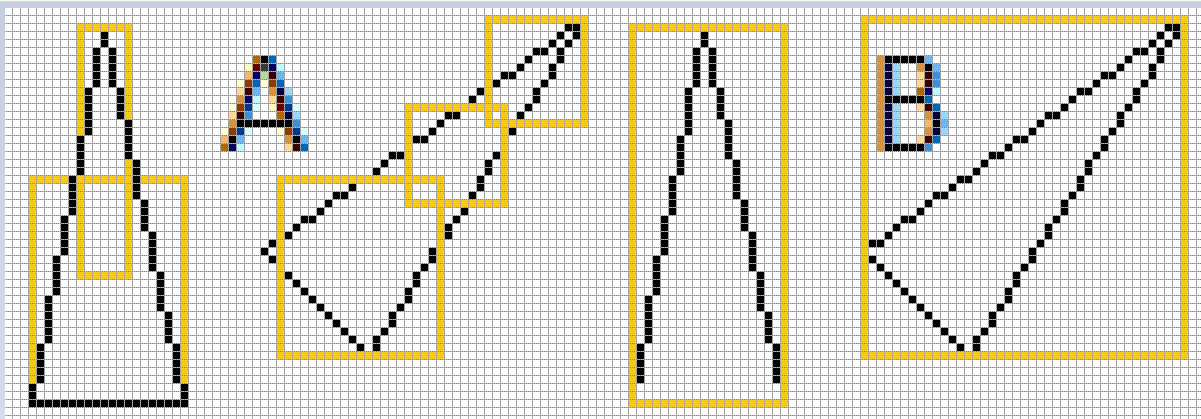
Sin embargo tenemos que tener especial cuidado con objetos oblongos, En esos casos, si nos limitamos a calcular un hitbox que contenga todo el objeto, su área puede ser mucho mayor, y la posibilidad de falsas colisiones aumenta mucho (B).

Para evitar eso se pueden crear hitboxes mixtas, compuestas de varios rectángulos, de modo que el área se mantenga más o menos constante y el hitbox combinado contenga la mayor parte del objeto.

Detectar colisiones con hitboxes rectangulares

SDL 2 nos proporciona funciones para calcular y verificar intersecciones entre rectángulos y entre un rectángulo y una línea.

Como es habitual, tenemos versiones para coordenadas en coma flotante y enteras.

La función SDL_HasIntersection verifica si dos rectángulos se intersecan, con coordenadas enteras.

La función SDL_HasIntersectionF hace lo mismo pero con coordenadas en coma flotante.

La función SDL_IntersectRect hace lo mismo que SDL_HasIntersection, pero además devuelve en el tercer parámetro un puntero al rectángulo de intersección.

SDL_IntersectFRect hace lo mismo, pero con coordenadas en coma flotante.

Por último, SDL_IntersectRectAndLine calcula las coordenadas de inicio y final del segmento de una línea que se interseca con un rectángulo, con coordenadas enteras.

Y SDL_IntersectFRectAndLine, lo mismo, pero con coordenadas en coma flotante.

Para el cálculo de colisiones usaremos las funciones SDL_HasIntersection o SDL_HasIntersectionF, dependiendo de si usamos coordenadas enteras o en coma flotante, respectivamente. No nos interesa conocer el rectángulo de intersección, tan solo si se intersecan o no.

Si las hitboxes de dos objetos vienen dadas por los rectángulos r1 y r2, tendremos una colisión cuando:

bool colision = SDL_HasIntersectionF(&r1, &r2);

Detectar colisiones con hitboxes circulares

Calcular colisiones de objetos usando hitboxes circulares también es sencillo. Para cada hitbox solo necesitamos las coordenadas del centro y el radio. Tendremos una colisión cuando la distancia entre los centros sea menor que la suma de los radios.

Para calcular la distancia entre dos puntos tan solo hay que aplicar el teorema de Pitágoras. Tenemos un triángulo rectángulo en el que la distancia es la hipotenusa, y los catetos miden cada uno la diferencia de las coordenadas en los ejes x e y.

d = √((dx1-dx2)2 + (dy1-dy2)2)

Podemos evitar el cálculo de raíces cuadradas si comparamos el valor de d² con el cuadrado de la suma de los radios de los hitboxes. Siempre es más rápido para la cpu calcular un cuadrado que una raíz.

Si las coordenadas de los hitboxes son los puntos (p1.x, p1.y) y (p2.x, p2.y), y sus radios r1 y r2, tendremos una colisión cuando:

bool colision = ((r1+r2)*(r1+r2)) >= ((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));

Detectar colisiones con hitboxes circulares y rectangulares

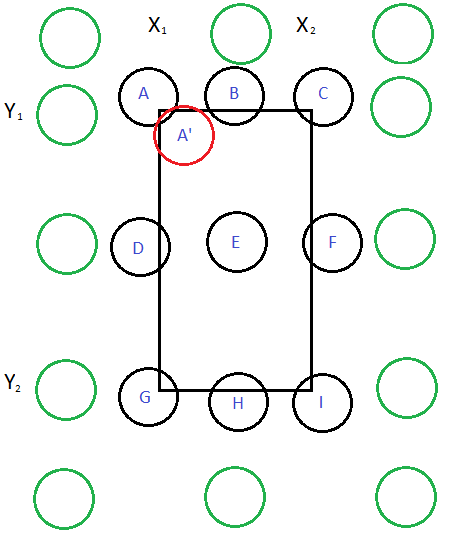
En la figura de la derecha vemos que hay nueve posibles casos de colisión entre un círculo y un rectángulo.

Fijémonos primero en el caso A. En el caso extremo solo la esquina superior izquierda del rectángulo estará dentro del círculo, por lo tanto, solo tendremos que verificar si ese punto está dentro del círculo para detectar la colisión, es decir, si la distancia del punto (x1, y1) al centro del círculo (x, y) es menor que el radio del círculo.

El caso C, G e I son similares, pero con las otras tres esquinas del rectángulos, es decir, los puntos (x2, y1), (x1, y2) y (x2, y2).

Ahora veamos el caso B. De nuevo, el caso extremo es que solo el punto del borde del rectángulo inmediatamente debajo del centro del círculo esté dentro del círculo. En ese caso, las coordenadas del punto a verificar serán (x, y1). Si su distancia al centro del círculo es menor que el radio, tendremos colisión.

Los casos D, F y H son similares, pero con los puntos (x1, y), (x2, y) y (x, y2), respectivamente.

En el caso E todo el círculo está en el interior del rectángulo, así que podemos usar cualquier punto del círculo, y el más evidente es su centro, cuya distancia al centro es cero, que es menor que el radio.

¿Qué pasa con el caso A'? la esquina del rectángulo está fuera del círculo, y sin embargo, el circulo colisiona con el rectángulo. Podemos considerarlo un caso general del caso E, en el que el centro del círculo está dentro del rectángulo. Así como los posibles casos C', G' e I'.

Recapitulemos:

• Empecemos tomando como punto de prueba el centro del círculo (x, y).
• Si x<x1 tomaremos como coordenada x el valor x1.
• Si x>x2 tomaremos como coordenada x el valor x2.
• Si y<y1 tomaremos como coordenada y el valor y1.
• Si y>y2 tomaremos como coordenada y el valor y2.
• Tendremos colisión si la distancia del punto de prueba al centro del círculo es menor que el radio.

// p(x,y) centro del circulo, r radio
// r(x, y, w, h)
pt = p; // Punto de prueba es el centro del circulo
if(pt.x < r.x) pt.x = r.x;
if(pt.x > r.x+r.w) pt.x = r.x+r.w;
if(pt.y < r.y) pt.y = r.y;
if(pt.y > r.y+r.h) pt.y = r.y+r.h;
return ((pt.x-p.x)*(pt.x-p.x)+(pt.y-p.y)*(pt.y-p.y)) <= r*r;

Este algoritmo funciona aunque el círculo sea más grande que el rectángulo. Si dos, tres o las cuatro esquinas del rectángulo están dentro del círculo siempre se verificará si cualquiera de ellas están dentro del círculo, y basta que haya una para que se detecte la colisión.

Calcular hitbox

A la hora de determinar las hitboxes de los objetos del juego se pueden dar dos casos:

• Que las hitboxes puedan mantenerse durante todo el juego para determinados objetos, ya sea porque no cambian de forma o de orientación, o porque esos cambios no afecten a las hitboxes. En este caso las podremos definir en la fase de diseño.
• Que las hitboxes no puedan mantenerse. En este caso habrá que recalcularlas cada vez que el objeto cambie de forma o de orientación.

Tendremos que aceptar ciertos compromisos.

Si la forma de un objeto es muy irregular podemos dividir la hitbox en varias, de modo que la orientación o el cambio de forma no afecten demasiado.

Por otra parte, tendremos que asumir que ciertas partes del objeto puedan quedar fuera del hitbox, y ciertas partes que no pertenecen al objeto queden dentro del hitbox. Es decir, se detectarán falsas colisiones y no se detectarán ciertas colisiones.

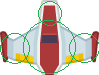
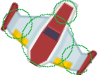
Pongamos por ejemplo la imagen de la derecha. Hemos dividido el hitbox en cuatro círculos. Esto tiene la ventaja de que aunque el objeto gire, si giramos los círculos en el mismo ángulo, las partes cubiertas por el hitbox serán prácticamente las mismas.

Evidentemente, hay partes del objeto fuera del hitbox, como las puntas de las alas, y el hitbox contiene zonas que no pertenecen al objeto, pero es un compromiso aceptable entre precisión y la complicación de dividir en más partes el hitbox.

Casos especiales

Si nuestro bucle de juego es lo suficientemente rápido, y las velocidades a las que se mueven nuestros objetos no son excesivas, no deberíamos tener problemas para detectar colisiones.

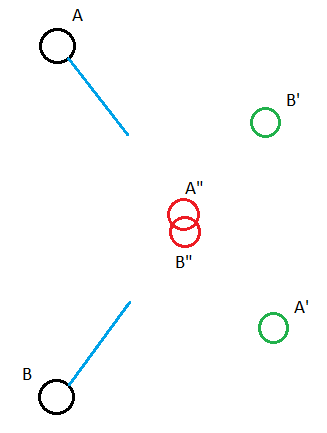
Pero puede que esto no sea siempre así. Si no se cumple cualquiera de las dos condiciones anteriores puede suceder que entre iteraciones sucesivas del bucle del juego dos objetos se crucen sin que hayamos detectado una colisión. Esto será más frecuente si los objetos en cuestión son pequeños y se mueven lo bastante rápido.

Por ejemplo, en la imagen de la derecha en la primera iteración del bucle los objetos están en las posiciones A y B, y en la siguiente iteración en A' y B'. Nuestro bucle nunca ha pasado por el punto de colisión, A" y B", por lo que no ha podido detectar esa colisión.

Nuestra primera opción puede ser depurar y optimizar nuestro bucle, de modo que se ejecute más frecuentemente, pero esto no siempre será posible, y aún puede suceder que determinadas iteraciones del bucle requieran más tiempo por causas ajenas a nuestro programa.

Una segunda opción es limitar la velocidad de los objetos para que nunca puedan moverse tan rápido, pero esto puede afectar seriamente a la experiencia de determinados juegos.

Una tercera opción puede ser recurrir a los cálculos. Calcular el punto de intersección de las trayectorias y verificar si los dos objetos alcanzan ese punto en el mismo momento.

La cuarta opción es modificar las hitboxes, aunque esto puede ser muy complejo dependiendo de las trayectorias.

Cualquiera que sea la opción elegida entre estas dos últimas, la posición actual de los objetos A' y B' no será válida, y tendremos que recalcular todo en función del punto de colisión calculado, con las consecuencias en cascada que eso puede provocar. Todo esto afecta al bucle del juego, y empeora los procesos para detectar colisiones en la siguiente iteración.

De modo que intentaremos evitar estas situaciones en lo posible, o conformarnos con no detectar estas colisiones y seguir el programa como si no currieran.

Asteroids 2

Nuestra nave está muy sola en el espacio, y el espacio demasiado vacío.

Fondo de estrellas

Empecemos añadiendo un poco de decoración, nada que influya en la mecánica del juego, solo que añada algo que lo haga más agradable.

Tendremos que añadir un método a nuestra clase Renderer para pintar puntos:

    void DrawPoint(FPoint punto) {
        SDL_RenderDrawPointF(renderer, punto.X(), punto.Y());
    }

Y para añadir algunas estrellas, añadiremos un nuevo valor, un vector de puntos estrellas, y añadiremos en el constructor 500 estrellas aleatorias.

class Asteroides : public sdl::Game {
private:
...
    std::vector<sdl::FPoint> estrellas;
...
        for(int i=0; i<500; i++) {
            estrellas.push_back({static_cast<float>(w*rand()/RAND_MAX), static_cast<float>(h*rand()/RAND_MAX)});
        }
...

Asteroides

Ahora vamos a colocar algunos asteroides. El juego original empieza con cinco asteroides grandes, así que haremos lo mismo.

Necesitamos un gráfico vectorial para nuestros asteroides, pero no nos complicaremos la vida demasiado: todos los asteroides del mismo tamaño tendrán la misma forma, aunque podremos cambiar esto en el futuro si lo consideramos adecuado.

Tomamos como centro el punto (18,18) y obtenemos las coordenadas de los puntos.

Hacemos lo mismo con los asteroides medianos y pequeños, y guardaremos todos los puntos en un vector de vectores de puntos:

static const std::vector<std::vector<sdl::FPoint>> asteroide = {
    {{-5.0, -18.0}, {10.0, -16.0}, {19.0, -3.0}, {10.0, 7.0}, {11.0, 15.0}, {-5.0, 19.0}, {-18.0,8.0}, {-14.0, -7.0}, {-5.0, -18.0} },
    {{-10.0, -14.0}, {2.0, -14.0}, {11.0, 1.0}, {14.0, 1.0}, {8.0, 9.0}, {-2.0, 14.0}, {-9.0,6.0}, {-14.0, 4.0}, {-9.0, -5.0}, {-10.0,-14.0} },
    {{-4.0, -10.0}, {2.0, -10.0}, {9.0, -6.0}, {5.0, 1.0}, {8.0, 5.0}, {0.0, 9.0}, {-5.0,-2.0}, {-7.0, -4.0}, {-4.0, -10.0} }};

También crearemos un tipo enumerado para los diferentes tipos de asteroides:

enum tipoAsteroide {
    grande=0,
    mediano,
    pequeno,
    nada
};

Ahora crearemos una nueva clase para manipular asteroides.

Necesitamos almacenar algunos valores:

• El tipo, o tamaño del asteroide tipo del tipo enumerado tipoAsteroide.
• Su posicion actual, de tipo FPoint.
• Su velocidad, que es un vector también de tipo FPoint.
• El ángulo de giro actual, alfa de tipo float.
• Y la velocidad de rotación vRotacion, también float.
• Por último, necesitaremos un vector de puntos con las coordenadas trasladadas en función de los parámetros anteriores y el tiempo.

El método para trasladar los puntos del gráfico es análogo al de la nave.

El constructor crea un asteroide en las coordenadas dadas y del tamaño indicado, y le asigna un vector de velocidad y una velocidad de giro aleatorios.

El método Actualizar calcula la nueva posición del asteroide en función de sus parámetros y del tiempo transcurrido desde la actualización anterior.

El método Puntos obtiene una referencia a los puntos del gráfico para pasarlos al renderer.

A la clase Asteroides que maneja el juego, le añadimos un vector de objetos Asteroide:

class Asteroides : public sdl::Game {
private:
...
    std::vector<Asteroide> asteroides;

En el método Init insertamos los asteroides iniciales:

void Asteroides::Init() {
    // Añadir 5 asteroides grandes
    for(int i=0; i<5; i++) {
        asteroides.push_back(Asteroide({static_cast<float>(640.0*rand()/RAND_MAX), 
                static_cast<float>(480.0*rand()/RAND_MAX)}, grande));
    }
}

En el método Update actualizamos las posiciones de todos los asteroides:

    for(size_t i=0; i<asteroides.size(); i++) asteroides[i].Actualizar(tick, escala);

Y en Render mostramos los asteroides:

    // Asteroides:
    for(size_t i=0; i<asteroides.size(); i++) {
        renderer.SetDrawColor(0,255,0,255);
        renderer.DrawLinesF(asteroides[i].Puntos());
    }

Añadiendo físicas a los asteroides

En la versión original del juego los asteroides solo podían interactuar con la nave del jugador y con los disparos.

Nosotros añadiremos más complicación, y haremos que los asteroides también puedan chocar entre ellos, y además queremos que sus trayectorias después del choque sigan algunas leyes físicas.

He añadido un artículo en el blog sobre el cálculo de trayectorias de colisiones. Aplicaremos esos cálculos asumiendo que las colisiones entre asteroides son elásticas.

Para empezar, tenemos que detectar colisiones entre asteroides. Y debido a la forma que tienen, lo mejor será usar hitboxes circulares, por lo que nuestros algoritmos de detección de colisiones también tendrán que manejar círculos.

Añadiremos nuevas clases para manejar círculos, aunque sólo la que usa valores en coma flotante servirá para usarse en hitboxes:

class Circle {
protected:
    Point center;
    int radius;
public:
    Circle(int x=0, int y=0, int r=0) : center(x, y), radius(r) {}
    Circle(Point &c, int r=0) : center(c), radius(r) {}
    Point &Center() { return center; }
    int &X() { return center.X(); }
    int &Y() { return center.Y(); }
    int &R() { return radius; }
};

class FCircle {
protected:
    FPoint center;
    float radius;
public:
    FCircle(float x=0, float y=0, float r=0) : center(x, y), radius(r) {}
    FCircle(FPoint &c, float r=0) : center(c), radius(r) {}
    FCircle Move(float alfa, sdl::FPoint &displacement, sdl::FPoint &escale) {
        // x' = x * x" * cos(α) + y * y" * sin(α) + dx
        // y' = -x * x" * sin(α) + y * y" * cos(α) + dy
        return {escale.X()*center.X() * static_cast<float>(cos(alfa)) +
                escale.Y()*center.Y() * static_cast<float>(sin(alfa)) + escale.X()*displacement.X(),
                -escale.X()*center.X() * static_cast<float>(sin(alfa)) +
                escale.Y()*center.Y() * static_cast<float>(cos(alfa)) + escale.Y()*displacement.Y(),
                escale.X()*radius};
    }
    FPoint &Center() { return center; }
    float &X() { return center.X(); }
    float &Y() { return center.Y(); }
    float &R() { return radius; }
};

También crearemos una clase para manejar hitboxes, y una clase auxiliar para manejar diferentes formas de hitbox: rectangulares o circulares:

enum shapeType {
    rectangle=0,
    circle
};

class Shape {
protected:
    shapeType type;
    union {
        FRect re;
        FCircle ci;
    };
public:
    Shape() : type(rectangle), re({0,0,0,0}) {}
    Shape(FCircle c) : type(circle), ci(c) {}
    Shape(FRect r) : type(rectangle), re(r) {}
    Shape Move(float alfa, sdl::FPoint &displacement, sdl::FPoint &escale);
    FCircle &Ci() { return ci; }
    FRect &&Re() { return re; }
    friend class Hitbox;
};

Shape Shape::Move(float alfa, sdl::FPoint &displacement, sdl::FPoint &escale) {
    FPoint point;

    if(type == circle) {
        point = ci.Center().Move(alfa, displacement, escale);
        return Shape(FCircle(point, ci.R()*escale.X()));
    }
    //rectangulo:
    point = re.Corner().Move(alfa, displacement, escale);
    return Shape(FRect(point.X(), point.Y(), re.W()*escale.X(), re.H()*escale.Y()));
}

class Hitbox {
protected:
    std::vector<Shape> hitbox; // formas de hitbox normalizadas
    std::vector<Shape> hitboxT; // hitbox trasladadas
    bool CollisionCircleCircle(FCircle &c1, FCircle &c2);
    bool CollisionRectRect(FRect &r1, FRect &r2);
    bool CollisionRectCircle(FRect &r1, FCircle &ci);

public:
    Hitbox() {}
    void ResizeT() { hitboxT.resize(hitbox.size()); }
    void InsertShape(const Shape &f) { hitbox.push_back(f); }
    bool Collision(Hitbox &);
    void Move(float alfa, sdl::FPoint &displacement, sdl::FPoint &escale);
    void Reset() {
        hitbox.clear();
    }
    Shape GetShape(int i) { return hitboxT[i]; }
};

La clase Shape puede almacenar tanto rectángulos como círculos. Necesitaremos trasladar los hitboxes a la misma posición y ángulo que los objetos a los que están asociados, así que también necesitan un método de Move.

La clase Hitbox mantiene dos copias de las formas, una con la posición normalizada del hitbox, en las coordenadas (0,0), y con orientación en el eje x, y otra asociada a la posición actual de objeto.

El método InsertShape se usa para añadir las diferentes formas que definen un hitbox. Puede ser solo una o varias.

El método ResizeT es necesario para que los dos vectores de formas tengan el mismo tamaño desde el inicio.

El método Colision devolverá true si el objeto actual colisiona con el del parámetro. En esta versión solo se detectan colisiones entre formas circulares, pero iremos completando este comportamiento en futuras versiones.

En nuestro juego tendremos que añadir las formas iniciales para los hitboxes de los asteroides:

static const std::vector<std::vector<sdl::Shape>> forma = {
    { sdl::FCirculo(0, 0, 19) },
    { sdl::FCirculo(0, 0, 14) },
    { sdl::FCirculo(0, 0, 10) }
};

En la clase Asteroide añadiremos un nuevo miembro:

    sdl::Hitbox hitbox;

Modificaremos el constructor para inicializar el hitbox:

    Asteroide(const sdl::FPoint &pos, tipoAsteroide t) : tipo(t), posicion(pos), alfa(360.0*std::rand()/RAND_MAX) {
        asteroide2.resize(asteroide[tipo].size());
        float v = 100.0*std::rand()/RAND_MAX;
        alfa = 2.0*pi*std::rand()/RAND_MAX;
        velocidad = {v*(float)cos(alfa), v*(float)sin(alfa)};
        vRotacion = -5.0+10.0*std::rand()/RAND_MAX;
        for(size_t i=0; i<forma[tipo].size(); i++) hitbox.InsertShape(forma[tipo][i]);
        hitbox.ResizeT();
    }

También tendremos que añadir en el método Actualizar el traslado del hitbox a la misma posición que el asteroide.

Por último, añadiremos un método para detectar la colisión con otro asteroide:

    bool Colision(Asteroide &a) {
        return hitbox.Collision(a.hitbox);
    }

En cuanto a la clase Asteroides, añadiremos el miembro que contiene los asteroides. Debe ser un vector, ya que más adelante, cuando disparemos a los asteroides, algunos se dividirán, y será necesario añadir más asteroides.

    std::vector<Asteroide> asteroides;

Tendremos que modificar el método Init para añadir los cinco asteroides iniciales:

void Asteroides::Init() {
    // Añadir 5 asteroides grandes
    for(int i=0; i<5; i++) {
        asteroides.push_back(Asteroide({static_cast<float>(640.0*rand()/RAND_MAX), static_cast<float>(480.0*rand()/RAND_MAX)}, grande));
    }
}

Y, por supuesto, el método Update para detectar colisiones y actuar en consecuencia.

void Asteroides::Update() {
    nave.Actualizar(tick, acelerar, alfa, escala);
    for(size_t i=0; i<asteroides.size(); i++) asteroides[i].Actualizar(tick, escala);
    // Detectar colisiones
    for(size_t i=0; i<asteroides.size()-1; i++) {
        for(size_t j=i+1; j<asteroides.size(); j++) {
            if(asteroides[i].Colision(asteroides[j])) {
                RebotarAsteroides(i, j);
            }
        }
    }
}

El método privado RebotarAsteroides calcula las nuevas velocidades de dos asteroides que colisionan elásticamente.

Tal como está ahora, en determinadas circunstancias, tenemos un comportamiento no esperado. Si dos asteroides chocan en ciertas condiciones (cerca del borde y con determinadas velocidades y direcciones) puede suceder que en la siguiente iteración se vuelva a detectar colisión, y se recalculen las velocidades, y este comportamiento se repita indefinidamente, quedando los dos asteroides en una especie de órbita.

Podemos minimizar esto añadiendo un parámetro a cada asteroide, de modo que si en la iteración anterior se detectó una colisión entre dos asteroides, en la siguiente (o en varias siguientes), colisiones entre esos dos asteroides se ignoren. Sin embargo, como los asteroides que desaparecen por uno de los bordes, aparecen en el contrario, siempre habrá una posibilidad de que dos asteroides se superpongan.

Otra alternativa es hacer que los asteroides también reboten contra los bordes, pero esto nos plantea un problema con la nave, ya que no tiene sentido que la nave rebote en los bordes y sí lo hagan los asteroides.

En siguientes pasos del juego tendremos que depurar la generación de las posiciones iniciales de los asteroides. No queremos que aparezcan varios en posiciones muy cercanas, ni tampoco demasiado cerca de la nave al iniciarse el juego.

Ejemplo Asteroides 2

Nombre	Fichero	Fecha	Tamaño	Contador	Descarga
Asteroides 2	sdl_asteroides2.zip	2024-07-03	10581 bytes	52