Capítulo 7 Árboles binarios de búsqueda (ABB)
7.1 Definición
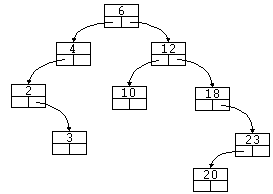
Se trata de árboles de orden 2 en los que se cumple que para cada nodo, el valor de la clave de la raíz del subárbol izquierdo es menor que el valor de la clave del nodo y que el valor de la clave raíz del subárbol derecho es mayor que el valor de la clave del nodo.
7.2 Operaciones en ABB
El repertorio de operaciones que se pueden realizar sobre un ABB es parecido al que realizábamos sobre otras estructuras de datos, más alguna otra propia de árboles:
- Buscar un elemento.
- Insertar un elemento.
- Borrar un elemento.
- Movimientos a través del árbol:
- Izquierda.
- Derecha.
- Raiz.
- Información:
- Comprobar si un árbol está vacío.
- Calcular el número de nodos.
- Comprobar si el nodo es hoja.
- Calcular la altura de un nodo.
- Calcular la altura de un árbol.
7.3 Buscar un elemento
Partiendo siempre del nodo raíz, el modo de buscar un elemento se define de forma recursiva.
- Si el árbol está vacío, terminamos la búsqueda: el elemento no está en el árbol.
- Si el valor del nodo raíz es igual que el del elemento que buscamos, terminamos la búsqueda con éxito.
- Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo.
- Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho.
El valor de retorno de una función de búsqueda en un ABB puede ser un puntero al nodo encontrado, o NULL, si no se ha encontrado.
7.4 Insertar un elemento
Para insertar un elemento nos basamos en el algoritmo de búsqueda. Si el elemento está en el árbol no lo insertaremos. Si no lo está, lo insertaremos a continuación del último nodo visitado.
Necesitamos un puntero auxiliar para conservar una referencia al padre del nodo raíz actual. El valor inicial para ese puntero es NULL.
- Padre = NULL
- nodo = Raiz
- Bucle: mientras actual no sea un árbol vacío o hasta que se encuentre el elemento.
- Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo: Padre=nodo, nodo=nodo->izquierdo.
- Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho: Padre=nodo, nodo=nodo->derecho.
- Si nodo no es NULL, el elemento está en el árbol, por lo tanto salimos.
- Si Padre es NULL, el árbol estaba vacío, por lo tanto, el nuevo árbol sólo contendrá el nuevo elemento, que será la raíz del árbol.
- Si el elemento es menor que el Padre, entonces insertamos el nuevo elemento como un nuevo árbol izquierdo de Padre.
- Si el elemento es mayor que el Padre, entonces insertamos el nuevo elemento como un nuevo árbol derecho de Padre.
Este modo de actuar asegura que el árbol sigue siendo ABB.
7.5 Borrar un elemento
Para borrar un elemento también nos basamos en el algoritmo de búsqueda. Si el elemento no está en el árbol no lo podremos borrar. Si está, hay dos casos posibles:
- Se trata de un nodo hoja: en ese caso lo borraremos directamente.
- Se trata de un nodo rama: en ese caso no podemos eliminarlo, puesto que perderíamos todos los elementos del árbol de que el nodo actual es padre. En su lugar buscamos el nodo más a la izquierda del subárbol derecho, o el más a la derecha del subárbol izquierdo e intercambiamos sus valores. A continuación eliminamos el nodo hoja.
Necesitamos un puntero auxiliar para conservar una referencia al padre del nodo raíz actual. El valor inicial para ese puntero es NULL.
- Padre = NULL
- Si el árbol está vacío: el elemento no está en el árbol, por lo tanto salimos sin eliminar ningún elemento.
- (1) Si el valor del nodo raíz es igual que el del elemento que buscamos, estamos ante uno de los siguientes casos:
- El nodo raíz es un nodo hoja:
- Si 'Padre' es NULL, el nodo raíz es el único del árbol, por lo tanto el puntero al árbol debe ser NULL.
- Si raíz es la rama derecha de 'Padre', hacemos que esa rama apunte a NULL.
- Si raíz es la rama izquierda de 'Padre', hacemos que esa rama apunte a NULL.
- Eliminamos el nodo, y salimos.
- El nodo no es un nodo hoja:
- Buscamos el 'nodo' más a la izquierda del árbol derecho de raíz o el más a la derecha del árbol izquierdo. Hay que tener en cuenta que puede que sólo exista uno de esos árboles. Al mismo tiempo, actualizamos 'Padre' para que apunte al padre de 'nodo'.
- Intercambiamos los elementos de los nodos raíz y 'nodo'.
- Borramos el nodo 'nodo'. Esto significa volver a (1), ya que puede suceder que 'nodo' no sea un nodo hoja. (Ver ejemplo 3)
- Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo.
- Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho.
Ejemplo 1: Borrar un nodo hoja
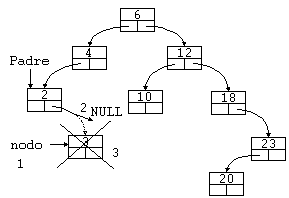
En el árbol de ejemplo, borrar el nodo 3.
- Localizamos el nodo a borrar, al tiempo que mantenemos un puntero a 'Padre'.
- Hacemos que el puntero de 'Padre' que apuntaba a 'nodo', ahora apunte a NULL.
- Borramos el 'nodo'.
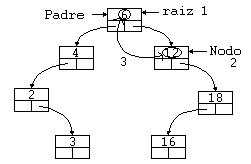
Ejemplo 2: Borrar un nodo rama con intercambio de un nodo hoja
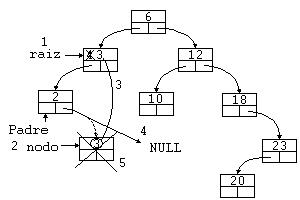
En el árbol de ejemplo, borrar el nodo 4.
- Localizamos el nodo a borrar ('raíz').
- Buscamos el nodo más a la derecha del árbol izquierdo de 'raíz', en este caso el 3, al tiempo que mantenemos un puntero a 'Padre' a 'nodo'.
- Intercambiamos los elementos 3 y 4.
- Hacemos que el puntero de 'Padre' que apuntaba a 'nodo', ahora apunte a NULL.
- Borramos el 'nodo'.
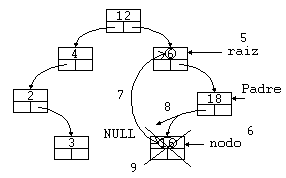
Ejemplo 3: Borrar un nodo rama con intercambio de un nodo rama
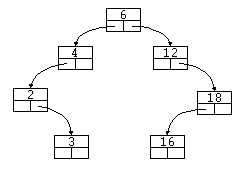
Para este ejemplo usaremos otro árbol. En éste borraremos el elemento 6.
- Localizamos el nodo a borrar ('raíz').
- Buscamos el nodo más a la izquierda del árbol derecho de 'raíz', en este caso el 12, ya que el árbol derecho no tiene nodos a su izquierda, si optamos por la rama izquierda, estaremos en un caso análogo. Al mismo tiempo que mantenemos un puntero a 'Padre' a 'nodo'.
- Intercambiamos los elementos 6 y 12.
- Ahora tenemos que repetir el bucle para el nodo 6 de nuevo, ya que no podemos eliminarlo.
- Localizamos de nuevo el nodo a borrar ('raíz').
- Buscamos el nodo más a la izquierda del árbol derecho de 'raíz', en este caso el 16, al mismo tiempo que mantenemos un puntero a 'Padre' a 'nodo'.
- Intercambiamos los elementos 6 y 16.
- Hacemos que el puntero de 'Padre' que apuntaba a 'nodo', ahora apunte a NULL.
- Borramos el 'nodo'.
Este modo de actuar asegura que el árbol sigue siendo ABB.
7.6 Movimientos a través del árbol
No hay mucho que contar. Nuestra estructura se referenciará siempre mediante un puntero al nodo Raiz, este puntero no debe perderse nunca.
Para movernos a través del árbol usaremos punteros auxiliares, de modo que desde cualquier puntero los movimientos posibles serán: moverse al nodo raíz de la rama izquierda, moverse al nodo raíz de la rama derecha o moverse al nodo Raiz del árbol.
7.7 Información
Hay varios parámetros que podemos calcular o medir dentro de un árbol. Algunos de ellos nos darán idea de lo eficientemente que está organizado o el modo en que funciona.
Comprobar si un árbol está vacío
Un árbol está vacío si su raíz es NULL.
Calcular el número de nodos.
Tenemos dos opciones para hacer esto, una es llevar siempre la cuenta de nodos en el árbol al mismo tiempo que se añaden o eliminan elementos. La otra es, sencillamente, contarlos.
Para contar los nodos podemos recurrir a cualquiera de los tres modos de recorrer el árbol: inorden, preorden o postorden, como acción sencillamente incrementamos el contador.
Comprobar si el nodo es hoja
Esto es muy sencillo, basta con comprobar si tanto el árbol izquierdo como el derecho están vacíos. Si ambos lo están, se trata de un nodo hoja.
Calcular la altura de un nodo
No hay un modo directo de hacer esto, ya que no nos es posible recorrer el árbol en la dirección de la raíz. De modo que tendremos que recurrir a otra técnica para calcular la altura.
Lo que haremos es buscar el elemento del nodo de que queremos averiguar la altura. Cada vez que avancemos un nodo incrementamos la variable que contendrá la altura del nodo.
- Empezamos con el nodo raíz apuntando a Raiz, y la 'Altura' igual a cero.
- Si el valor del nodo raíz es igual que el del elemento que buscamos, terminamos la búsqueda y el valor de la altura es 'Altura'.
- Incrementamos 'Altura'.
- Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo.
- Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho.
Calcular la altura de un árbol
La altura del árbol es la altura del nodo de mayor altura. Para buscar este valor tendremos que recorrer todo el árbol, de nuevo es indiferente el tipo de recorrido que hagamos, cada vez que cambiemos de nivel incrementamos la variable que contiene la altura del nodo actual, cuando lleguemos a un nodo hoja compararemos su altura con la variable que contiene la altura del árbol si es mayor, actualizamos la altura del árbol.
- Iniciamos un recorrido del árbol en postorden, con la variable de altura igual a cero.
- Cada vez que empecemos a recorrer una nueva rama, incrementamos la altura para ese nodo.
- Después de procesar las dos ramas, verificamos si la altura del nodo es mayor que la variable que almacena la altura actual del árbol, si es así, actualizamos esa variable.
7.8 árboles degenerados
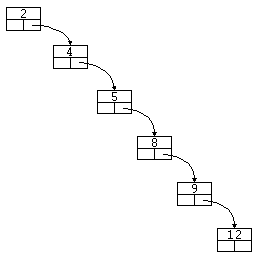
Los árboles binarios de búsqueda tienen un gran inconveniente. Por ejemplo, supongamos que creamos un ABB a partir de una lista de valores ordenada:
2, 4, 5, 8, 9, 12
Difícilmente podremos llamar a la estructura resultante un árbol.
Esto es lo que llamamos un árbol binario de búsqueda degenerado, y en el siguiente capítulo veremos una nueva estructura, el árbol AVL, que resuelve este problema, generando árboles de búsqueda equilibrados.
7.9 Ejemplo de ABB en C
Vamos a ver cómo implementar en C algunas de las funciones que hemos explicado para árboles ABB, al final se incluye un ejemplo completo para árboles de enteros.
Declaración de tipos
Como estamos trabajando con un árbol binario, sólo necesitamos una estructura para referirnos tanto a cualquiera de los nodos como al árbol completo. Recuerda que cualquier nodo puede ser considerado como la raíz de un árbol.
typedef struct _nodo {
int dato;
struct _nodo *derecho;
struct _nodo *izquierdo;
} tipoNodo;
typedef tipoNodo *pNodo;
typedef tipoNodo *Arbol;
Insertar un elemento en un árbol ABB
Diseñaremos una función que se ajuste al algoritmo que describimos en el punto 7.4:
- Padre = NULL
- nodo = Raiz
- Bucle: mientras actual no sea un árbol vacío o hasta que se encuentre el elemento.
- Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo: Padre=nodo, nodo=nodo->izquierdo.
- Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho: Padre=nodo, nodo=nodo->derecho.
- Si nodo no es NULL, el elemento está en el árbol, por lo tanto salimos.
- Si Padre es NULL, el árbol estaba vacío, por lo tanto, el nuevo árbol sólo contendrá el nuevo elemento, que será la raíz del árbol.
- Si el elemento es menor que el Padre, entonces insertamos el nuevo elemento como un nuevo árbol izquierdo de Padre.
- Si el elemento es mayor que el Padre, entonces insertamos el nuevo elemento como un nuevo árbol derecho de Padre.
void Insertar(Arbol *a, int dat) {
pNodo padre = NULL; /* (1) */
pNodo actual = *a; /* (2) */
while(!Vacio(actual) && dat != actual->dato) { /* (3) */
padre = actual;
if(dat < actual->dato) actual = actual->izquierdo; /* (3-a) */
else if(dat > actual->dato) actual = actual->derecho; /* (3-b) */
}
if(!Vacio(actual)) return; /* (4) */
if(Vacio(padre)) { /* (5) */
*a = (Arbol)malloc(sizeof(tipoNodo));
(*a)->dato = dat;
(*a)->izquierdo = (*a)->derecho = NULL;
}
else if(dat < padre->dato) { /* (6) */
actual = (Arbol)malloc(sizeof(tipoNodo));
padre->izquierdo = actual;
actual->dato = dat;
actual->izquierdo = actual->derecho = NULL;
}
else if(dat > padre->dato) { /* (7) */
actual = (Arbol)malloc(sizeof(tipoNodo));
padre->derecho = actual;
actual->dato = dat;
actual->izquierdo = actual->derecho = NULL;
}
}
Eliminar un elemento de un árbol ABB
Diseñaremos una función que se ajuste al algoritmo que describimos en el punto 7.5:
- Padre = NULL
- Si el árbol está vacío: el elemento no está en el árbol, por lo tanto salimos sin eliminar ningún elemento.
- Si el valor del nodo raíz es igual que el del elemento que buscamos, estamos ante uno de los siguientes casos:
- El nodo raíz es un nodo hoja:
- Si 'Padre' es NULL, el nodo raíz es el único del árbol, por lo tanto el puntero al árbol debe ser NULL.
- Si raíz es la rama derecha de 'Padre', hacemos que esa rama apunte a NULL.
- Si raíz es la rama izquierda de 'Padre', hacemos que esa rama apunte a NULL.
- Eliminamos el nodo, y salimos.
- El nodo no es un nodo hoja:
- Buscamos el 'nodo' más a la izquierda del árbol derecho de raíz o el más a la derecha del árbol izquierdo. Hay que tener en cuenta que puede que sólo exista uno de esos árboles. Al mismo tiempo, actualizamos 'Padre' para que apunte al padre de 'nodo'.
- Intercambiamos los elementos de los nodos raíz y 'nodo'.
- Borramos el nodo 'nodo'. Esto significa volver a (3), ya que puede suceder que 'nodo' no sea un nodo hoja.
- Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo.
- Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho.
void Borrar(Arbol *a, int dat) {
pNodo padre = NULL; /* (1) */
pNodo actual;
pNodo nodo;
int aux;
actual = *a;
while(!Vacio(actual)) { /* Búsqueda (2) else implícito */
if(dat == actual->dato) { /* (3) */
if(EsHoja(actual)) { /* (3-a) */
if(padre)/* (3-a-i caso else implícito) */
if(padre->derecho == actual) padre->derecho = NULL; /* (3-a-ii) */
else if(padre->izquierdo == actual) padre->izquierdo = NULL; /* (3-a-iii) */
free(actual); /* (3-a-iv) */
actual = NULL;
return;
}
else { /* (3-b) */
/* Buscar nodo */
padre = actual; /* (3-b-i) */
if(actual->derecho) {
nodo = actual->derecho;
while(nodo->izquierdo) {
padre = nodo;
nodo = nodo->izquierdo;
}
}
else {
nodo = actual->izquierdo;
while(nodo->derecho) {
padre = nodo;
nodo = nodo->derecho;
}
}
/* Intercambio */
aux = actual->dato; /* (3-b-ii) */
actual->dato = nodo->dato;
nodo->dato = aux;
actual = nodo;
}
}
else {
padre = actual;
if(dat > actual->dato) actual = actual->derecho; /* (4) */
else if(dat < actual->dato) actual = actual->izquierdo; /* (5) */
}
}
}
Buscar un elemento en un árbol ABB
Diseñaremos una función que se ajuste al algoritmo que describimos en el punto 7.3:
- Si el árbol está vacío, terminamos la búsqueda: el elemento no está en el árbol.
- Si el valor del nodo raíz es igual que el del elemento que buscamos, terminamos la búsqueda con éxito.
- Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo.
- Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho.
int Buscar(Arbol a, int dat) {
pNodo actual = a;
while(!Vacio(actual)) {
if(dat == actual->dato) return TRUE; /* dato encontrado (2) */
else if(dat < actual->dato) actual = actual->izquierdo; /* (3) */
else if(dat > actual->dato) actual = actual->derecho; /* (4) */
}
return FALSE; /* No está en árbol (1) */
}
Comprobar si el árbol está vacío
Esta función es fácil de implementar:
int Vacio(Arbol r) {
return r==NULL;
}
Comprobar si un nodo es hoja
Esta función también es sencilla de implementar:
int EsHoja(pNodo r) {
return !r->derecho && !r->izquierdo;
}
Contar número de nodos
En el punto 7.7 comentábamos que para contar los nodos podemos recurrir a cualquiera de los tres modos de recorrer el árbol: inorden, preorden o postorden y como acción incrementamos el contador de nodos. Para implementar este algoritmo recurrimos a dos funciones:
int NumeroNodos(Arbol a, int *contador) {
*contador = 0;
auxContador(a, contador);
return *contador;
}
void auxContador(Arbol nodo, int *c) {
(*c)++; /* Acción: incrementar número de nodos. (Preorden) */
if(nodo->izquierdo) auxContador(nodo->izquierdo, c); /* Rama izquierda */
if(nodo->derecho) auxContador(nodo->derecho, c); /* Rama derecha */
}
Calcular la altura de un árbol
Es un problema parecido al anterior, pero ahora tenemos que contar la altura, no en número de nodos. Cada vez que lleguemos a un nodo hoja, verificamos si la altura del nodo es la máxima, y si lo es, actualizamos la altura del árbol a ese valor:
- Iniciamos un recorrido del árbol en postorden, con la variable de altura igual a cero.
- Cada vez que empecemos a recorrer una nueva rama, incrementamos la altura para ese nodo.
- Después de procesar las dos ramas, verificamos si la altura del nodo es mayor que la variable que almacena la altura actual del árbol, si es así, actualizamos esa variable.
int AlturaArbol(Arbol a, int *altura) {
*altura = 0; /* (1) */
auxAltura(a, 0, altura);
return *altura;
}
void auxAltura(pNodo nodo, int a, int *altura) {
/* (2) Cada vez que llamamos a auxAltura pasamos como parámetro a+1 */
if(nodo->izquierdo) auxAltura(nodo->izquierdo, a+1, altura); /* Rama izquierda */
if(nodo->derecho) auxAltura(nodo->derecho, a+1, altura); /* Rama derecha */
if(EsHoja(nodo) && a > *altura) *altura = a; /* Proceso (Postorden) (3) */
}
Calcular la altura del nodo que contiene un dato concreto
Lo que haremos será buscar el elemento del nodo del que queremos averiguar la altura. Cada vez que avancemos un nodo incrementamos la variable que contendrá la altura del nodo.
- Empezamos con el nodo raíz apuntando a Raiz, y la 'Altura' igual a cero.
- Si el valor del nodo raíz es igual que el del elemento que buscamos, terminamos la búsqueda y el valor de la altura es 'Altura'.
- Incrementamos 'Altura'.
- Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo.
- Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho.
int Altura(Arbol a, int dat) {
int altura = 0;
pNodo actual = a; /* (1) */
while(!Vacio(actual)) {
if(dat == actual->dato) return altura; /* dato encontrado. (2) */
else {
altura++; /* (3) */
if(dat < actual->dato) actual = actual->izquierdo; /* (4) */
else if(dat > actual->dato) actual = actual->derecho; /* (5) */
}
}
return -1; /* No está en árbol */
}
Aplicar una función a cada elemento del árbol, según los tres posibles recorridos
Todos los recorridos se aplican de forma recursiva. En este ejemplo crearemos tres funciones, una por cada tipo de recorrido, que aplicarán una función al elemento de cada nodo.
La función a aplicar puede ser cualquiera que admita como parámetro un puntero a un entero, y que no tenga valor de retorno.
InOrden
En Inorden, primero procesamos el subárbol izquierdo, después el nodo actual, y finalmente el subárbol derecho:
void InOrden(Arbol a, void (*func)(int*)) {
if(a->izquierdo) InOrden(a->izquierdo, func); /* Subárbol izquierdo */
func(&(a->dato)); /* Aplicar la función al dato del nodo actual */
if(a->derecho) InOrden(a->derecho, func); /* Subárbol derecho */
}
PreOrden
En Preorden, primero procesamos el nodo actual, después el subárbol izquierdo, y finalmente el subárbol derecho:
void PreOrden(Arbol a, void (*func)(int*)) {
func(&(a->dato)); /* Aplicar la función al dato del nodo actual */
if(a->izquierdo) PreOrden(a->izquierdo, func); /* Subárbol izquierdo */
if(a->derecho) PreOrden(a->derecho, func); /* Subárbol derecho */
}
PostOrden
En Postorden, primero procesamos el subárbol izquierdo, después el subárbol derecho, y finalmente el nodo actual:
void PostOrden(Arbol a, void (*func)(int*)) {
if(a->izquierdo) PostOrden(a->izquierdo, func); /* Subárbol izquierdo */
if(a->derecho) PostOrden(a->derecho, func); /* Subárbol derecho */
func(&(a->dato)); /* Aplicar la función al dato del nodo actual */
}
Fichero con el código fuente
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Ejemplo de árbol binario de búsqueda en C | arbolabb_c.zip | 2002-04-12 | 2748 bytes | 945 |
7.10 Ejemplo de ABB en C++
Haremos ahora lo mismo que en el ejemplo en C, pero incluyendo todas las funciones y datos en una única clase.
Declaración de clase ArbolABB
Declaramos dos clases, una para nodo y otra para ArbolABB, la clase nodo la declararemos como parte de la clase ArbolABB, de modo que no tendremos que definir relaciones de amistad, y evitamos que otras clases o funciones tengan acceso a los datos internos de nodo.
class ArbolABB {
private:
//// Clase local de Lista para Nodo de ArbolBinario:
class Nodo {
public:
// Constructor:
Nodo(const int dat, Nodo *izq=NULL, Nodo *der=NULL) :
dato(dat), izquierdo(izq), derecho(der) {}
// Miembros:
int dato;
Nodo *izquierdo;
Nodo *derecho;
};
// Punteros de la lista, para cabeza y nodo actual:
Nodo *raíz;
Nodo *actual;
int contador;
int altura;
public:
// Constructor y destructor básicos:
ArbolABB() : raíz(NULL), actual(NULL) {}
~ArbolABB() { Podar(raíz); }
// Insertar en árbol ordenado:
void Insertar(const int dat);
// Borrar un elemento del árbol:
void Borrar(const int dat);
// Función de búsqueda:
bool Buscar(const int dat);
// Comprobar si el árbol está vacío:
bool Vacio(Nodo *r) { return r==NULL; }
// Comprobar si es un nodo hoja:
bool EsHoja(Nodo *r) { return !r->derecho && !r->izquierdo; }
// Contar número de nodos:
const int NumeroNodos();
const int AlturaArbol();
// Calcular altura de un int:
int Altura(const int dat);
// Devolver referencia al int del nodo actual:
int &ValorActual() { return actual->dato; }
// Moverse al nodo raíz:
void Raiz() { actual = raíz; }
// Aplicar una función a cada elemento del árbol:
void InOrden(void (*func)(int&) , Nodo *nodo=NULL, bool r=true);
void PreOrden(void (*func)(int&) , Nodo *nodo=NULL, bool r=true);
void PostOrden(void (*func)(int&) , Nodo *nodo=NULL, bool r=true);
private:
// Funciones auxiliares
void Podar(Nodo* &);
void auxContador(Nodo*);
void auxAltura(Nodo*, int);
};
Definición de las funciones miembro
Las definiciones de las funciones miembro de la clase no difieren demasiado de las que creamos en C. Tan solo se han sustituido algunos punteros por referencias, y se usa el tipo bool cuando es aconsejable.
Por ejemplo, en las funciones de recorrido de árboles, la función invocada acepta ahora una referencia a un entero, en lugar de un puntero a un entero.
Fichero con el código fuente
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Ejemplo de árbol binario de búsqueda en C++ | arbolabb_cpp.zip | 2002-04-12 | 2796 bytes | 1011 |
7.11 Ejemplo de ABB en C++ usando plantillas
Sólo nos queda generalizar la clase del ejemplo anterior implementándola en forma de plantilla.
El proceso es relativamente sencillo, sólo tenemos que cambiar la declaración de dato, y todas sus referencias. Además de cambiar la sintaxis de las definiciones de las funciones, claro.
Declaración de la plantilla ArbolABB
Se trata de una simple generalización de la clase del punto anterior:
template<class DATO>
class ABB {
private:
//// Clase local de Lista para Nodo de ArbolBinario:
template<class DATON>
class Nodo {
public:
// Constructor:
Nodo(const DATON dat, Nodo<DATON> *izq=NULL, Nodo<DATON> *der=NULL) :
dato(dat), izquierdo(izq), derecho(der) {}
// Miembros:
DATON dato;
Nodo<DATON> *izquierdo;
Nodo<DATON> *derecho;
};
// Punteros de la lista, para cabeza y nodo actual:
Nodo<DATO> *raíz;
Nodo<DATO> *actual;
int contador;
int altura;
public:
// Constructor y destructor básicos:
ABB() : raíz(NULL), actual(NULL) {}
~ABB() { Podar(raíz); }
// Insertar en árbol ordenado:
void Insertar(const DATO dat);
// Borrar un elemento del árbol:
void Borrar(const DATO dat);
// Función de búsqueda:
bool Buscar(const DATO dat);
// Comprobar si el árbol está vacío:
bool Vacio(Nodo<DATO> *r) { return r==NULL; }
// Comprobar si es un nodo hoja:
bool EsHoja(Nodo<DATO> *r) { return !r->derecho && !r->izquierdo; }
// Contar número de nodos:
const int NumeroNodos();
const int AlturaArbol();
// Calcular altura de un dato:
int Altura(const DATO dat);
// Devolver referencia al dato del nodo actual:
DATO &ValorActual() { return actual->dato; }
// Moverse al nodo raíz:
void Raiz() { actual = raíz; }
// Aplicar una función a cada elemento del árbol:
void InOrden(void (*func)(DATO&) , Nodo<DATO> *nodo=NULL, bool r=true);
void PreOrden(void (*func)(DATO&) , Nodo<DATO> *nodo=NULL, bool r=true);
void PostOrden(void (*func)(DATO&) , Nodo<DATO> *nodo=NULL, bool r=true);
private:
// Funciones auxiliares
void Podar(Nodo<DATO>* &);
void auxContador(Nodo<DATO>*);
void auxAltura(Nodo<DATO>*, int);
};
Definición de las funciones miembro
Las definiciones de las funciones miembro de la clase no difieren en nada de las que creamos en el ejemplo anterior. Tan solo se han sustituido los tipos del dato por el tipo de dato de la plantilla.
Fichero con el código fuente
| Nombre | Fichero | Fecha | Tamaño | Contador | Descarga |
|---|---|---|---|---|---|
| Ejemplo de árbol binario de búsqueda con plantillas | arbolabb_templ.zip | 2002-04-12 | 3539 bytes | 934 |