12 Tipos de objetos IV: Punteros 1

No, no salgas corriendo todavía. Aunque vamos a empezar con un tema que suele asustar a los estudiantes de C++, no es algo tan terrible como se cuenta. Como se suele decir de los leones: no son tan fieros como los pintan.

Vamos a intentar explicar cómo funcionan los punteros de forma que no tengan el aspecto de magia negra ni un galimatías incomprensible.

Pero no bastará con entender lo que se explica en este capítulo. Es relativamente sencillo saber qué son y cómo funcionan los punteros. Para poder manejarlos es necesario también comprender los punteros, y eso significa saber qué pueden hacer y cómo lo hacen. Para comprender los punteros se necesita práctica, algunos necesitamos más que otros, (y yo considero que no me vendría mal seguir practicando). Incluso cuando ya creas que los dominas, seguramente quedarán nuevos matices por conocer.

Pero seguramente estoy exagerando. Si soy capaz de explicar correctamente los conceptos de este capítulo, pronto te encontrarás usando punteros en tus programas casi sin darte cuenta.

Los punteros proporcionan la mayor parte de la potencia al C++, y marcan la principal diferencia con otros lenguajes de programación.

Una buena comprensión y un buen dominio de los punteros pondrá en tus manos una herramienta de gran potencia. Un conocimiento mediocre o incompleto te impedirá desarrollar programas eficaces.

Por eso le dedicaremos mucha atención y mucho espacio a los punteros. Es muy importante comprender bien cómo funcionan y cómo se usan.

Creo que todos sabemos lo que es un puntero, fuera del ámbito de la programación. Usamos punteros para señalar cosas sobre las que queremos llamar la atención, como marcar puntos en un mapa o detalles en una presentación en pantalla. A menudo, usamos el dedo índice para señalar direcciones o lugares sobre los que estamos hablando o explicando algo. Cuando un dedo no es suficiente, podemos usar punteros. Antiguamente esos punteros eran una vara de madera, pero actualmente se usan punteros laser, aunque la idea es la misma. Un puntero también es el símbolo que representa la posición del ratón en una pantalla gráfica. Estos punteros también se usan para señalar objetos: enlaces, opciones de menú, botones, etc. Un puntero sirve, pues, para apuntar a los objetos a los que nos estamos refiriendo.

Pues en C++ un puntero es exactamente lo mismo. Probablemente habrás notado que a lo largo del curso nos hemos referido a variables, constantes, etc como objetos. Esto ha sido intencionado por el siguiente motivo:

C++ está diseñado para la programación orientada a objetos (POO), y en ese paradigma, todas las entidades que podemos manejar son objetos.

Los punteros en C++ sirven para señalar objetos, y también para manipularlos.

Para entender qué es un puntero veremos primero cómo se almacenan los datos en un ordenador.

La memoria de un ordenador está compuesta por unidades básicas llamadas bits. Cada bit sólo puede tomar dos valores, normalmente denominados alto y bajo, ó 1 y 0. Pero trabajar con bits no es práctico, y por eso se agrupan.

Cada grupo de 8 bits forma un byte u octeto. En realidad el microprocesador, y por lo tanto nuestro programa, sólo puede manejar directamente bytes o grupos de dos o cuatro bytes. Para acceder a los bits hay que acceder antes a los bytes.

Cada byte de la memoria de un ordenador tiene una dirección, llamada dirección de memoria.

Los microprocesadores trabajan con una unidad básica de información, a la que se denomina palabra (en inglés word). Dependiendo del tipo de microprocesador una palabra puede estar compuesta por uno, dos, cuatro, ocho o dieciséis bytes. Hablaremos en estos casos de plataformas de 8, 16, 32, 64 ó 128 bits. Se habla indistintamente de direcciones de memoria, aunque las palabras sean de distinta longitud. Cada dirección de memoria contiene siempre un byte. Lo que sucederá cuando las palabras sean, por ejemplo, de 32 bits es que accederemos a posiciones de memoria que serán múltiplos de 4.

Por otra parte, la mayor parte de los objetos que usamos en nuestros programas no caben en una dirección de memoria. La solución utilizada para manejar objetos que ocupen más de un byte es usar posiciones de memoria correlativas. De este modo, la dirección de un objeto es la dirección de memoria de la primera posición que contiene ese objeto.

Dicho de otro modo, si para almacenar un objeto se precisan cuatro bytes, y la dirección de memoria de la primera posición es n, el objeto ocupará las posiciones desde n a n+3, y la dirección del objeto será, también, n.

Todo esto sucede en el interior de la máquina, y nos importa relativamente poco. Pero podemos saber qué tipo de plataforma estamos usando averiguando el tamaño del tipo int, y para ello hay que usar el operador sizeof, por ejemplo:

cout << "Plataforma de " << 8*sizeof(int) << " bits";

Ahora veamos cómo funcionan los punteros. Un puntero es un tipo especial de objeto que contiene, ni más ni menos que, la dirección de memoria de un objeto. Por supuesto, almacenada a partir de esa dirección de memoria puede haber cualquier clase de objeto: un char, un int, un float, un array, una estructura, una función u otro puntero. Seremos nosotros los responsables de decidir ese contenido, al declarar el puntero.

De hecho, podríamos decir que existen tantos tipos diferentes de punteros como tipos de objetos puedan ser referenciados mediante punteros. Si tenemos esto en cuenta, los punteros que apunten a tipos de objetos distintos, serán tipos diferentes. Por ejemplo, no podemos asignar a un puntero a char el valor de un puntero a int.

Intentemos ver con mayor claridad el funcionamiento de los punteros. Podemos considerar la memoria del ordenador como un gran array, de modo que podemos acceder a cada celda de memoria a través de un índice. Podemos considerar que la primera posición del array es la 0 celda[0].

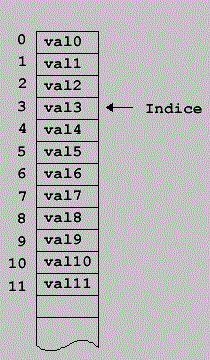
Si usamos una variable para almacenar el índice, por ejemplo, indice=0, entonces celda[0] == celda[indice]. Finalmente, si prescindimos de la notación de los arrays, podemos ver que el índice se comporta exactamente igual que un puntero.

El puntero indice podría tener por ejemplo, el valor 3, en ese caso, el valor apuntado por indice tendría el valor 'val3'.

Las celdas de memoria tienen una existencia física, es decir son algo real y existirán siempre, independientemente del valor del puntero. Existirán incluso si no existe el puntero.

De forma recíproca, la existencia o no existencia de un puntero no implica la existencia o la inexistencia del objeto. De la misma forma que el hecho de no señalar a un árbol, no implica la inexistencia del árbol. Algo más oscuro es si tenemos un puntero para árboles, que no esté señalando a un árbol. Un puntero de ese tipo no tendría uso si estamos en medio del mar: tener ese puntero no crea árboles de forma automática cuando señalemos con él. Es un puntero, no una varita mágica. :-D

Del mismo modo, el valor de la dirección que contiene un puntero no implica que esa dirección sea válida, en el sentido de que no tiene por qué contener la dirección de un objeto del tipo especificado por el puntero.

Supongamos que tenemos un mapa en la pared, y supongamos también que existen diferentes tipos de punteros láser para señalar diferentes tipos de puntos en el mapa (ya sé que esto suena raro, pero usemos la imaginación). Creamos un puntero para señalar ciudades. Nada más crearlo (o encenderlo), el puntero señalará a cualquier sitio, podría señalar incluso a un punto fuera del mapa. En general, daremos por sentado que una vez creado, el puntero no tiene por qué apuntar a una ciudad, y aunque apunte al mapa, podría estar señalando a un mar o a un río.

Con los punteros en C++ ocurre lo mismo. El valor inicial del puntero, cuando se declara, podría estar fuera del mapa, es decir, contener direcciones de memoria que no existen. Pero, incluso señalando a un punto de la memoria, es muy probable que no señale a un objeto del tipo adecuado. Debemos considerar esto como el caso más probable, y no usar jamás un puntero que no haya sido inicializado correctamente.

Dentro del array de celdas de memoria existirán zonas que contendrán programas y datos, tanto del usuario como del propio sistema operativo o de otros programas, el sistema operativo se encarga de gestionar esa memoria, prohibiendo o protegiendo determinadas zonas.

Pero el propio puntero, como objeto que es, también se almacenará en memoria, y por lo tanto, también tendrá una dirección de memoria. Cuando declaramos un puntero estaremos reservando la memoria necesaria para almacenarlo, aunque, como pasa con el resto del los objetos, el contenido de esa memoria contendrá basura.

En principio, debemos asignar a un puntero, o bien la dirección de un objeto existente, o bien la de uno creado explícitamente durante la ejecución del programa o un valor conocido que indique que no señala a ningún objeto, es decir el valor 0. El sistema operativo, cuanto más avanzado es, mejor suele controlar la memoria. Ese control se traduce en impedir el acceso a determinadas direcciones reservadas por el sistema.

Declaración de punteros

Los punteros se declaran igual que el resto de los objetos, pero precediendo el identificador con un asterisco (*).

Sintaxis:

<tipo> *<identificador>; 

Ejemplos:

int *pEntero;
char *pCaracter;
struct stPunto *pPunto;

Los punteros sólo pueden apuntar a objetos de un tipo determinado, en el ejemplo, pEntero sólo puede apuntar a un objeto de tipo int.

La forma:

<tipo>* <identificador>;

con el (*) junto al tipo, en lugar de junto al identificador del objeto, también está permitida. De hecho, también es legal la forma:

<tipo> * <identificador>;

Veamos algunos matices. Tomemos el primer ejemplo:

int *pEntero;

equivale a:

int* pEntero;

Otro detalle importante es que, aunque las tres formas de situar el asterisco en la declaración son equivalentes, algunas de ellas pueden inducirnos a error, sobre todo si se declaran varios objetos en la misma línea:

int* x, y;

En este caso, x es un puntero a int, pero y no es más que un objeto de tipo int. Colocar el asterisco junto al tipo puede que indique más claramente que estamos declarando un puntero, pero hay que tener en cuenta que sólo afecta al primer objeto declarado, si quisiéramos declarar ambos objetos como punteros a int tendremos que hacerlo de otro modo:

int* x, *y;
// O:
int *x, *y;
// O:
int* x;
int* y;

Obtener punteros a objetos

Los punteros apuntan a objetos, por lo tanto, lo primero que tenemos que saber hacer con nuestros punteros es asignarles direcciones de memoria válidas de objetos.

Para averiguar la dirección de memoria de cualquier objeto usaremos el operador de dirección (&), que leeremos como "dirección de".

Por supuesto, los tipos tienen que ser "compatibles", no podemos almacenar la dirección de un objeto de tipo char en un puntero de tipo int.

Por ejemplo:

int A;
int *pA;

pA = &A;

Según este ejemplo, pA es un puntero a int que apunta a la dirección donde se almacena el valor del entero A.

Objeto apuntado por un puntero

La operación contraria es obtener el objeto referenciado por un puntero, con el fin de manipularlo, ya sea modificando su valor u obteniendo el valor actual.

Para manipular el objeto apuntado por un puntero usaremos el operador de indirección, que es un asterisco (*).

En C++ es muy habitual que el mismo símbolo se use para varias cosas diferentes, este es el caso del asterisco, que se usa como operador de multiplicación, para la declaración de punteros y, como vemos ahora, como operador de indirección.

Como operador de indirección sólo está permitido usarlo con punteros, y podemos leerlo como "objeto apuntado por".

Por ejemplo:

int *pEntero;
int x = 10;
int y;

pEntero = &y;
*pEntero = x; // (1)

En (1) asignamos al objeto apuntado por pEntero en valor del objeto x. Como pEntero apunta al objeto y, esta sentencia equivale (según la secuencia del programa), a asignar a y el valor de x.

Diferencia entre punteros y otros objetos

Debemos tener muy claro, en el ejemplo anterior, que pEntero es un objeto del tipo "puntero a int", pero que *pEntero NO es un objeto de tipo int, sino una expresión.

¿Por qué decimos esto?

Pues porque, como pasa con todos los objetos en C++, cuando se declaran sólo se reserva espacio para almacenarlos, pero no se asigna ningún valor inicial, (recuerda que nuestro puntero para árboles no crea árbol cada vez que señalemos con él). El contenido del objeto permanecerá sin cambios, de modo que el valor inicial del puntero será aleatorio e indeterminado. Debemos suponer que contiene una dirección no válida.

Si pEntero apunta a un objeto de tipo int, *pEntero será el contenido de ese objeto, pero no olvides que *pEntero es un operador aplicado a un objeto de tipo "puntero a int". Es decir, *pEntero es una expresión, no un objeto.

Declarar un puntero no creará un objeto del tipo al que apunta. Por ejemplo: int *pEntero; no crea un objeto de tipo int en memoria. Lo que crea es un objeto que puede contener la dirección de memoria de un entero.

Podemos decir que existe físicamente un objeto pEntero, y también que ese objeto puede (aunque esto no es siempre cierto) contener la dirección de un objeto de tipo int.

Como todos los objetos, los punteros también contienen "basura" cuando son declarados. Es costumbre dar valores iniciales nulos a los punteros que no apuntan a ningún sitio concreto:

int *pEntero = 0; // También podemos asignar el valor NULL
char *pCaracter = 0;

NULL es una constante, que está definida como cero en varios ficheros de cabecera, como "cstdio" o "iostream", y normalmente vale 0L. Sin embargo, hay muchos textos que recomiendan usar el valor 0 para asignar a punteros nulos, al menos en C++.

Correspondencia entre arrays y punteros

En muchos aspectos, existe una equivalencia entre arrays y punteros. De hecho, cuando declaramos un array estamos haciendo varias cosas a la vez:

• Declaramos un puntero del mismo tipo que los elementos del array.
• Reservamos memoria para todos los elementos del array. Los elementos de un array se almacenan internamente en la memoria del ordenador en posiciones consecutivas.
• Se inicializa el puntero de modo que apunte al primer elemento del array.

Las diferencias entre un array y un puntero son dos:

• Que el identificador de un array se comporta como un puntero constante, es decir, no podemos hacer que apunte a otra dirección de memoria.
• Que el compilador asocia, de forma automática, una zona de memoria para los elementos del array, cosa que no hace para los elementos apuntados por un puntero corriente.

Ejemplo:

int vector[10];
int *puntero;

puntero = vector; /* Equivale a puntero = &vector[0]; (1)
                     esto se lee como "dirección del primer elemento de vector" */
(*puntero)++;     /* Equivale a vector[0]++; (2) */
puntero++;        /* puntero equivale a asignar a puntero el valor &vector[1] (3) */

¿Qué hace cada una de estas instrucciones?:

En (1) se asigna a puntero la dirección del array, o más exactamente, la dirección del primer elemento del array vector.

En (2) se incrementa el contenido de la memoria apuntada por puntero, que es vector[0].

En (3) se incrementa el puntero, esto significa que apuntará a la posición de memoria del siguiente elemento int, y no a la siguiente posición de memoria. Es decir, el puntero no se incrementará en una unidad, como tal vez sería lógico esperar, sino en la longitud de un int, ya que puntero apunta a un objeto de tipo int.

Análogamente, la operación:

puntero = puntero + 7;

No incrementará la dirección de memoria almacenada en puntero en siete posiciones, sino en 7*sizeof(int).

Otro ejemplo:

struct stComplejo {
   float real, imaginario;
} Complejo[10];
stComplejo *pComplejo;  /* Declaración de un puntero */

pComplejo = Complejo; /* Equivale a pComplejo = &Complejo[0]; */
pComplejo++;          /* pComplejo  == &Complejo[1] */

En este caso, al incrementar pComplejo avanzaremos las posiciones de memoria necesarias para apuntar al siguiente complejo del array Complejo. Es decir avanzaremos sizeof(stComplejo) bytes.

La correspondencia entre arrays y punteros también afecta al operador []. Es decir, podemos usar los corchetes con punteros, igual que los usamos con arrays. Pero incluso podemos ir más lejos, ya que es posible usar índices negativos.

Por ejemplo, las siguientes expresiones son equivalentes:

   *(puntero + 7);
   puntero[7];

De forma análoga, el siguiente ejemplo también es válido:

   int vector[10];
   int *puntero;

   puntero = &vector[5];
   puntero[-2] = puntero[2] = 100;

Evidentemente, nunca podremos usar un índice negativo con un array, ya que estaríamos accediendo a una zona de memoria que no pertenece al array, pero eso no tiene por qué ser cierto con punteros.

En este último ejemplo, puntero apunta al sexto elemento de vector, de modo que puntero[-2] apunta al cuarto, es decir, vector[3] y puntero[2] apunta al octavo, es decir, vector[7].

Operaciones con punteros

La aritmética de punteros es limitada, pero en muchos aspectos muy interesante; y aunque no son muchas las operaciones que se pueden hacer con los punteros, cada una tiene sus peculiaridades.

Asignación

Ya hemos visto cómo asignar a un puntero la dirección de una variable. También podemos asignar un puntero a otro, esto hará que los dos apunten a la misma dirección de memoria:

int *q, *p;
int a;

q = &a; /* q apunta a la dirección de a */
p = q;  /* p apunta al mismo sitio, es decir,
           a la dirección de a */

Sólo hay un caso especial en la asignación de punteros, y es cuando se asigna el valor cero. Este es el único valor que se puede asignar a cualquier puntero, independientemente del tipo de objeto al que apunte.

Operaciones aritméticas

Podemos distinguir dos tipos de operaciones aritméticas con punteros. En uno de los tipos uno de los operandos es un puntero, y el otro un entero. En el otro tipo, ambos operandos son punteros.

Ya hemos visto ejemplos del primer caso. Cada unidad entera que se suma o resta al puntero hace que este apunte a la dirección del siguiente objeto o al anterior, respectivamente, del mismo tipo.

El valor del entero, por lo tanto, no se interpreta como posiciones de memoria física, sino como posiciones de objetos del tipo al que apunta el puntero.

Por ejemplo, si sumamos el valor 2 a un puntero a int, y el tipo int ocupa cuatro bytes, el puntero apuntará a la dirección ocho bytes mayor a la original. Si se tratase de un puntero a char, el puntero avanzará dos posiciones de memoria.

Las restas con enteros operan de modo análogo.

Con este tipo de operaciones podemos usar los operadores de suma, resta, preincremento, postincremento, predecremento y postdecremento. Además, podemos combinar los operadores de suma y resta con los de asignación: += y -=.

En cuanto al otro tipo de operaciones aritméticas, sólo está permitida la resta, ya que la suma de punteros no tiene sentido. Si la suma o resta de un puntero y un entero da como resultado un puntero, la resta de dos punteros dará como resultado, lógicamente, un entero. Veamos un ejemplo:

int vector[10];
int *p, *q;

p = vector; /* Equivale a p = &vector[0]; */
q = &vector[4]; /* apuntamos al 5º elemento */
cout << q-p << endl;

El resultado será 4, que es la "distancia" entre ambos punteros.

Generalmente, este tipo de operaciones sólo tendrá sentido entre punteros que apunten a objetos del mismo tipo, y más frecuentemente, entre punteros que apunten a elementos del mismo array.

Comparación entre punteros

Comparar punteros puede tener sentido en la misma situación en la que lo tiene restar punteros, es decir, averiguar posiciones relativas entre punteros que apunten a elementos del mismo array. Podemos usar los operadores <, <=, >= o > para averiguar posiciones relativas entre objetos del mismo tipo apuntados por punteros.

Existe otra comparación que se realiza muy frecuente con los punteros. Para averiguar si estamos usando un puntero nulo es corriente hacer la comparación:

if(NULL != p)

Lo expuesto en el capítulo 9 sobre conversiones implícitas a bool también se aplica a punteros, de modo que podemos simplificar esta sentencia como:

if(p)

Y también:

if(NULL == p)

O simplemente:

if(!p)

Nota: No es posible comparar punteros de tipos diferentes, ni aunque ambos sean nulos.

Punteros genéricos

Es posible declarar punteros sin especificar a qué tipo de objeto apuntan:

void *<identificador>;

Usaremos estos punteros en situaciones donde podemos referirnos a distintos tipos de objetos, ya que podemos hacer que apunten a objetos de cualquier tipo.

Por supuesto, para eso tendremos que hacer un casting con punteros, sintaxis:

(<tipo> *)<variable puntero>

Por ejemplo:

#include <iostream>
using namespace std;

int main() {
   char cadena[10] = "Hola";
   char *c;
   int *n;
   void *v;

   c = cadena; // c apunta a cadena
   n = (int *)cadena; // n también apunta a cadena
   v = (void *)cadena; // v también
   cout << "carácter: " << *c << endl;
   cout << "entero:   " << *n << endl;
   cout << "float:    " << *(float *)v << endl;
   return 0;
}

El resultado será:

carácter: H
entero:   1634496328
float:    2.72591e+20 

Vemos que tanto cadena como los punteros n, c y v apuntan a la misma dirección, pero cada puntero tratará la información que encuentre allí de modo diferente, para c es un carácter y para n un entero. Para v no tiene tipo definido, pero podemos hacer casting con el tipo que queramos, en este ejemplo con float.

Punteros a estructuras

Los punteros también pueden apuntar a estructuras. En este caso, para referirse a cada elemento de la estructura se usa el operador (->), en lugar del (.).

Ejemplo:

#include <iostream>
using namespace std;

struct stEstructura {
   int a, b;
} estructura, *e;

int main() {
   estructura.a = 10;
   estructura.b = 32;
   e = &estructura;

   cout << "puntero" << endl;
   cout << e->a << endl;
   cout << e->b << endl;
   cout << "objeto" << endl;
   cout << estructura.a << endl;
   cout << estructura.b << endl;

   return 0;
}

Ejemplos

Veamos algunos ejemplos de cómo trabajan los punteros.

Primero un ejemplo que ilustra la diferencia entre un array y un puntero:

#include <iostream>
using namespace std;

int main() {
   char cadena1[] = "Cadena 1";
   char *cadena2 = "Cadena 2";

   cout << cadena1 << endl;
   cout << cadena2 << endl;

   //cadena1++; // Ilegal, cadena1 es constante
   cadena2++; // Legal, cadena2 es un puntero

   cout << cadena1 << endl;
   cout << cadena2 << endl;

   cout << cadena1[1] << endl;
   cout << cadena2[0] << endl;

   cout << cadena1 + 2 << endl;
   cout << cadena2 + 1 << endl;

   cout << *(cadena1 + 2) << endl;
   cout << *(cadena2 + 1) << endl;

   return 0;
}

Aparentemente, y en la mayoría de los casos, cadena1 y cadena2 son equivalentes, sin embargo hay operaciones que están prohibidas con los arrays, ya que son punteros constantes.

Otro ejemplo:

#include <iostream>
using namespace std;

int main() {
   char Mes[][11] = { "Enero", "Febrero", "Marzo", "Abril",
      "Mayo", "Junio", "Julio", "Agosto",
      "Septiembre", "Octubre", "Noviembre", "Diciembre"};
   const char *Mes2[] = { "Enero", "Febrero", "Marzo", "Abril",
      "Mayo", "Junio", "Julio", "Agosto",
      "Septiembre", "Octubre", "Noviembre", "Diciembre"};

   cout << "Tamaño de Mes: " << sizeof(Mes) << endl;
   cout << "Tamaño de Mes2: " << sizeof(Mes2) << endl;
   cout << "Tamaño de cadenas de Mes2: "
        << &Mes2[11][10]-Mes2[0] << endl;
   cout << "Tamaño de Mes2 + cadenas : "
        << sizeof(Mes2)+&Mes2[11][10]-Mes2[0] << endl;

   return 0;
}

En este ejemplo declaramos un array Mes de dos dimensiones que almacena 12 cadenas de 11 caracteres, 11 es el tamaño necesario para almacenar el mes más largo (en caracteres): "Septiembre".

Después declaramos Mes2 que es un array de punteros a char, para almacenar la misma información. La ventaja de este segundo método es que no necesitamos contar la longitud de las cadenas para calcular el espacio que necesitamos, cada puntero de Mes2 es una cadena de la longitud adecuada para almacenar el nombre de cada mes.

Parece que el segundo sistema es más económico en cuanto al uso de memoria, pero hay que tener en cuenta que además de las cadenas también en necesario almacenar los doce punteros.

El espacio necesario para almacenar los punteros lo dará la segunda línea de la salida. Y el espacio necesario para las cadenas lo dará la tercera línea.

Si las diferencias de longitud entre las cadenas fueran mayores, el segundo sistema sería más eficiente en cuanto al uso de la memoria.

Objetos dinámicos

El uso principal y más potente de los punteros es el manejo de la memoria dinámica.

La memoria se clasifica en muchas categorías, por ahora nos centraremos en algunas de ellas. Cuando se ejecuta un programa, el sistema operativo reserva una zona de memoria para el código o instrucciones del programa y otra para los objetos que se usan durante la ejecución. A menudo estas zonas son la misma, y componen lo que se denomina memoria local. También hay otras zonas de memoria, como la pila, que se usa, entre otras cosas, para intercambiar datos entre las funciones. El resto, la memoria que no se usa por ningún programa es lo que se conoce como heap o montón. Nuestro programa puede hacer uso de esa memoria durante la ejecución, de modo que la cantidad de espacio de memoria usado por el programa no está limitada por el diseño ni por las declaraciones de objetos realizadas en el código fuente. Por eso se denomina a este tipo, memoria dinámica, ya que tanto la cantidad de memoria como su uso se deciden durante la ejecución, y en general, cambia a lo largo del tiempo, de forma dinámica. Para ello, normalmente se usará memoria del montón, y no se llama así porque sea de peor calidad, sino porque suele haber un buen montón de memoria de este tipo.

C++ dispone de dos operadores para manejar (reservar y liberar) la memoria dinámica, son new y delete. En C estas acciones se realizan mediante funciones de la biblioteca estándar stdio.

Hay una regla de oro cuando se usa memoria dinámica: toda la memoria que se reserve durante el programa hay que liberarla antes de salir del programa. No seguir esta regla es una actitud muy irresponsable, y en la mayor parte de los casos tiene consecuencias desastrosas. No os fiéis de lo que diga el compilador, de que estas variables se liberan solas al terminar el programa, no siempre es verdad.

Veremos con mayor profundidad los operadores new y delete en el siguiente capítulo, por ahora veremos un ejemplo:

#include <iostream>
using namespace std;

int main() {
   int *a;
   char *b;
   float *c;
   struct stPunto {
      float x,y;
   } *d;

   a = new int;
   b = new char;
   c = new float;
   d = new stPunto;

   *a = 10;
   *b = 'a';
   *c = 10.32;
   d->x = 12; d->y = 15;

   cout << "a = " << *a << endl;
   cout << "b = " << *b << endl;
   cout << "c = " << *c << endl;
   cout << "d = (" << d->x << ", "
        << d->y << ")" << endl;

   delete a;
   delete b;
   delete c;
   delete d;

   return 0;
}

Y mucho cuidado: si pierdes un puntero a una variable reservada dinámicamente, no podrás liberarla.

Ejemplo:

int main()
{
   int *a;

   a = new int; // variable dinámica
   *a = 10;
   a = new int; // nueva variable dinámica,
                // se pierde el puntero a la anterior
   *a = 20;
   delete a;  // sólo liberamos la última reservada
   return 0;
}

En este ejemplo vemos cómo es imposible liberar la primera reserva de memoria dinámica. Lo correcto, si no la necesitábamos habría sido liberarla antes de reservar un nuevo bloque usando el mismo puntero, y si la necesitamos, habría que guardar su dirección, por ejemplo usando otro puntero.

Problemas

1. Escribir un programa con una función que calcule la longitud de una cadena de caracteres. El nombre de la función será LongitudCadena, debe devolver un int, y como parámetro de entrada debe tener un puntero a char.
   En esta función no se pueden usar enteros para recorrer el array, usar sólo punteros y aplicar aritmética de punteros.
   En main probar con distintos tipos de cadenas: arrays y punteros.
2. Escribir un programa con una función que busque un carácter determinado en una cadena. El nombre de la función será BuscaCaracter, debe devolver un int con la posición en que fue encontrado el carácter, si no se encontró volverá con -1. Los parámetros de entrada serán una cadena y un carácter. En la función main probar con distintas cadenas y caracteres.
3. Implementar en una función el siguiente algoritmo para ordenar un array de enteros.
   La idea es recorrer simultáneamente el array desde el principio y desde el final, comparando los elementos. Si los valores comparados no están en el orden adecuado, se intercambian y se vuelve a empezar el bucle. Si están bien ordenados, se compara el siguiente par.
   El proceso termina cuando los punteros se cruzan, ya que eso indica que hemos comparado la primera mitad con la segunda y todos los elementos estaban en el orden correcto.
   Usar una función con tres parámetros:
   void Ordenar(int* vector, int nElementos, bool ascendente);
   De nuevo, no se deben usar enteros, sólo punteros y aritmética de punteros.

Ejemplos capítulo 12

Ejemplo 12.1

Vamos a realizar un pequeño programa para trabajar con punteros.

Este ejemplo consiste en invertir el orden de los elementos de un vector de enteros, usando sólo puntetos, sin variables auxiliares enteras.

Para ello recorreremos el vector empezando por los dos extremos, e intercambiando cada par de elementos:

// Programa que invierte el orden de un vector
// Octubre de 2009 Con Clase, Salvador Pozo

#include <iostream>

using namespace std;

void Mostrar(int*, int);
void Intercambia(int*, int*);

int main() {
    int vector[10] = { 2,5,6,7,9,12,35,67,88,99 };
    int *p, *q;

    Mostrar(vector, 10); // Mostrar estado inicial

    p = vector;     // Primer elemento
    q = &vector[9]; // Ultimo elemento

    while(p < q) {  // Bucle de intercambio
        Intercambia(p++, q--);
    }
    Mostrar(vector, 10); // Mostrar estado final
    return 0;
}

void Mostrar(int *v, int n) {
    int *f = &v[n]; // Puntero a posición siguiente al último elemento
    while(v < f) {
        cout << *v << " ";
        v++;
    }
    cout << endl;
}

void Intercambia(int *p, int *q) {
    // Intercambiar sin usar variables auxiliares:
    *p += *q;
    *q = *p-*q;
    *p -= *q;
}

Ejecutar este código en OnlineGDB.

Probablemente parezca que nos hemos complicado la vida, pero se trata de un ejercicio.

Comentemos algunos detalles de este programa.

Primero, el bucle de intercambio. Hemos usado una única sentencia while. Como condición hemos usado la comparación de los dos punteros. Esto hace que el puntero p recorra la primera mitad del vector, empezando por el principio, y que q recorra la otra mitad, empezando por el final. El bucle se reperirá hasta que ambos punteros sean iguales, o hasta que se crucen. Si ambos punteros son iguales (esto sólo sucederá si el número de elementos es impar), los dos apuntarán al elemento central del vector, y no se producirá intercambio, lo cual no es un problema, ya que no hay nada que intercambiar.

La sentencia del bucle Intercambia(p++, q--); intercambiará los elementos apuntados por p y q, y posteriormente, incrementará p y decrementará q.

Hemos diseñado dos funciones auxiliares.

La primera Mostrar muestra el número de valores indicado en el segundo parámetro del vector suministrado mediante el primer parámetro.

He querido evitar, también en este caso, el uso de variables auxiliares de tipo int, aunque he decidido hacerlo usando un puntero auxiliar, que apunte a la dirección de un hipotético elemento n+1 del vector.

Podríamos habernos aprovechado de que los parámetros se pasan por valor, y usar el parámetro n como contador:

void Mostrar(int *v, int n) {
    while(n--) {
        cout << *v << " ";
        v++;
    }
    cout << endl;
}

Aunque este código tiene un problema potencial, si el valor inicial de n es cero o negativo el bucle no termina.

Podemos arreglar esto añadiendo una verificación inicial:

void Mostrar(int *v, int n) {
    if(n > 0) {
	    while(n--) {
            cout << *v << " ";
            v++;
        }
    }
    cout << endl;
}

La segunda función, Intercambia, como su nombre indica, intercambia los elementos del vector apuntados por los dos punteros pasados como parámetros.

También en este caso, y aprovechando que se trata de un vector de enteros, he querido evitar usar variables auxiliares. El truco consiste en mantener la información haciendo sumas y restas. Suponiendo que queremos intercambiar los valores n y m:

1. Sumamos los dos valores y guardamos el resultado en el primero. n=n+m
2. El nuevo valor de m es el resultado de restar del valor actual de n, el valor de m. Como n ahora contiene (n+m), el resultado será n+m-m = n. m=n-m
3. Por último, obtenemos el valor final de n restando de su valor actual (n+m) el valor actual de m (que es el valor original de n). n = n-m

Veamos un ejemplo:

N = 10, M = 3
1) N = N+M = 10+3 = 13   [N=13, M=3]
2) M = N-M = 13-3 = 10   [N=13, M=10]
3) N = N-M = 13-10 = 3   [N=3, M=10]

Esto sólo funciona con vectores de enteros. Con float podemos perder precisión en algunas operaciones, y con otros tipos, como estructuras o uniones, ni siquiera tiene sentido.

Ejemplo 12.2

Este ejemplo consiste en mezclar dos vectores ordenados en otro, de modo que también esté ordenado, como en el caso anterior usaremos sólo puntetos, sin variables auxiliares enteras.

Para ello recorreremos los dos vectores de entrada, empezando por el principio, e insertaremos el valor menor de cada uno, y tomaremos el siguiente:

// Programa que funde dos vectores ordenados
// Octubre de 2009 Con Clase, Salvador Pozo

#include <iostream>

using namespace std;

void Mostrar(int*, int);

int main() {
    int vector1[10] = { 3, 4, 6, 9, 12, 15, 17, 19, 22, 24 };
    int vector2[10] = { 1, 5, 8, 11, 13, 14, 21, 23, 25, 30 };
    int vectorR[20];

    int *p, *q, *r;
    int *u1, *u2;

    p = vector1;
    q = vector2;
    r = vectorR;
    u1 = &vector1[9];
    u2 = &vector2[9];

    cout << "Vectores de entrada:" << endl;
    Mostrar(vector1, 10);
    Mostrar(vector2, 10);

    while(p <= u1 && q <= u2) {
        if(*p < *q) { *r++ = *p++; }
        else        { *r++ = *q++; }
    }
    // Llegados a este punto, quedarán elementos por
    // copiar en uno de los vectores, así que hay
    // que copiarlos incondicionalmente:
    while(p <= u1) {
        *r++ = *p++;
    }
    while(q <= u2) {
        *r++ = *q++;
    }
    cout << "Resultado:" << endl;
    Mostrar(vectorR, 20);
    return 0;
}

void Mostrar(int *v, int n) {
    int *f = &v[n]; // Puntero a posición siguiente al último elemento
    while(v < f) {
        cout << *v << " ";
        v++;
    }
    cout << endl;
}

Ejecutar este código en OnlineGDB.

Hemos usado sólo punteros porque lo exige el enunciado, pero hubiera sido más lógico usar un índice parar recorrer los vectores de entrada.

Sin embargo, este método simplifica los movimientos de elementos entre los vectores de entrada y el de salida. En las expresiones del tipo *r++ = *p++; se evalúa primero la asignación, y después se incrementan los punteros, de modo que todo queda preparado para la siguiente iteración.

Ejemplo 12.3

Implementaremos ahora otro método de ordenación, que generalmente se usa con ficheros de disco secuenciales, pero que también se puede aplicar a vectores.

Nos centraremos ahora en el algoritmo de mezcla natural. Dada una lista de valores, en principio desordenada, este algoritmo consiste en copiar las secuencias ordenadas a otras listas, y después aplicar el método usado en el ejercicio anterior para obtener una lista más ordenada que la original. El proceso se repite hasta que sólo hay una secuencia en la lista.

Este método se puede usar con tantas listas auxiliares como se quiera, dos o más. Cuantas más listas auxiliares se usen, más rápidamente se ordenará la lista. El problema es que para cada nueva lista auxiliar se incrementa la cantidad de memoria necesaria, y sobre todo, la complejidad del programa.

Implementaremos este algoritmo con dos vectores auxiliares.

Pero veamos un ejemplo. Partamos del siguiente vector:

34 33 23 3 54 21 1 99 12 32 51 64

La primera etapa consiste en copiar elementos a los vectores auxiliares, alternando cada vez que se rompa una secuencia ordenada. En este caso, los dos vectores de salida quedarán:

34 23 21 12 32 51 64
33 3 54 1 99

A continuación, mezclamos los dos vectores, usando un algoritmo parecido al del ejemplo anterior. La diferencia es que nuestros vectores no están ordenados, y por lo tanto, las mezclas serán de subconjuntos de esos vectores:

33 34 3 23 21 54 1 12 32 51 64 99

Repetimos el proceso:

33 34 21 54
3 23 1 12 32 51 64 99

Y volvemos a mezclar:

3 23 33 34 1 12 21 32 51 54 64 99

Volvemos a repetir el proceso:

3 23 33 34
1 12 21 32 51 54 64 99

Y mezclamos otra vez:

1 3 12 21 23 32 33 34 51 54 64 99

Y la lista queda ordenada.

Tenemos que buscar una condición para detectar el final del proceso. Lo más sencillo es contar el número de secuencias ordenadas durante el proceso de mezcla. Si hay más de una, hay que repetir el proceso.

Sobre el papel es muy sencillo, pero no será tan fácil implementarlo. Veremos que necesitaremos un montón de variables auxiliares.

El proceso de separar los vectores es relativamente simple, pero veremos que mezclar los vectores resultantes no es tan sencillo, ya que sólo están parcialmente ordenados, y hay que mezclar cada par de fragmentos por separado.

Para cada vector auxiliar necesitamos tres punteros. Uno lo usaremos para recordar la dirección de inicio. Esto nos permitirá "rebobinar" el vector cada vez que tengamos que empezar a procesarlo y liberar su memoria cuando terminemos el trabajo. El segundo puntero lo usaremos para llenar el vector en el proceso de separar los fragmentos ordenados. Una vez terminado ese proceso, el puntero se usará para saber cuantos elementos contiene y para comparaciones cuando lo recorramos. El último puntero lo usaremos para recorrer el vector en la etapa de fusión de los vectores auxiliares.

El proceso de separar responde a este algoritmo:

El proceso de mezcla responde a este otro algoritmo:

Hemos tenido en cuenta todos los casos posibles. El caso A se dará cuando empecemos el proceso de fusión, y también cuando terminemos de fundir cada uno de las parejas de tramos.

Los casos B y C se darán cuando una de las listas termine, y queden elementos en la otra. Podríamos pensar que esto sólo va a suceder cuando termine la segunda, ya que el número de tramos será igual en ambas listas o habrá uno más en la primera que en la segunda. Sin embargo, cuando el número de tramos sea igual en ambas listas, puede que se termine de copiar primero los de la primera lista, quedando elementos por copiar en la segunda.

El D es el caso general, cuando quedan elementos en los fragmentos de las dos listas auxiliares. Se transfiere el menor de los dos.

Los casos E y F se dan cuando uno de los fragmentos se ha terminado, y se deben transferir los elementos que queden en el otro fragmento.

Finalmente, el caso G se da cuando los dos fragmentos se ha agotado. En ese caso comenzamos un nuevo tramo en la lista de salida. Si queda algún fragmento en alguna de las listas, volveremos a estar en el caso A, si no, habremos terminado.

La implementación es la siguiente:

// Ordenar usando el método de mezcla natural
// Octubre de 2009 Con Clase, Salvador Pozo

#include <iostream>

using namespace std;

void Mostrar(int*, int);
int MezclaNatural(int*, int);

int main() {
    int vector[12] = { 34, 33, 23, 3, 54, 21, 1, 99, 12, 32, 51, 64 };

    cout << "Vector inicial:" << endl;
    Mostrar(vector, 12);
    while(MezclaNatural(vector, 12) > 1);
    cout << "Vector final:" << endl;
    Mostrar(vector, 12);
    return 0;
}

void Mostrar(int *v, int n) {
    int *f = &v[n]; // Puntero a posición siguiente al último elemento
    while(v < f) {
        cout << *v << " ";
        v++;
    }
    cout << endl;
}

int MezclaNatural(int *v, int n) {
    int *aux[2];
    int *iaux[2];
    int *iaux2[2];
    int *i, *f;
    int activa=0; // Activamos el primer vector auxiliar
    int tramo;
    bool tramonuevo;

    aux[0] = iaux[0] = new int[12];
    aux[1] = iaux[1] = new int[12];
    i = v;
    f = &v[n];
    // El primer elemento se copia siempre al primer vector:
    *iaux[activa]++ = *i++;
    // Separar vector en auxiliares:
    while(i < f) {
        if(*i < *(i-1)) activa++;
        if(activa >=2) activa -= 2;
        *iaux[activa]++ = *i++;
    }

    // Fundir vectores auxiliares:
    iaux2[0] = aux[0];
    iaux2[1] = aux[1];
    i = v;
    tramo = 0;
    tramonuevo = true;
    while(iaux2[0] < iaux[0] || iaux2[1] < iaux[1]) {
        if(tramonuevo) { // caso A
            // El primer elemento lo añadimos directamente:
            if(*iaux2[0] < *iaux2[1]) { *i++ = *iaux2[0]++; }
            else                      { *i++ = *iaux2[1]++; }
            tramo++;
            tramonuevo = false;
        } else           // caso B
        if(iaux2[0] == iaux[0]) {
            while(iaux2[1] < iaux[1]) {
                if(*iaux2[1] < i[-1]) tramo++;
                *i++ = *iaux2[1]++;
            }
        } else           // caso C
        if(iaux2[1] == iaux[1]) {
            while(iaux2[0] < iaux[0]) {
                if(*iaux2[0] < i[-1]) tramo++;
                *i++ = *iaux2[0]++;
            }
        } else           // caso D
        if(*iaux2[0] > i[-1] && *iaux2[1] > i[-1]) {
            if(*iaux2[0] < *iaux2[1]) { *i++ = *iaux2[0]++; }
            else                      { *i++ = *iaux2[1]++; }
        } else           // caso E
        if(*iaux2[0] > i[-1])
            while(iaux2[0] < iaux[0] && *iaux2[0] > i[-1]) {
                *i++ = *iaux2[0]++;
            }
        else             // caso F
        if(*iaux2[1] > i[-1])
            while(iaux2[1] < iaux[1] && *iaux2[1] > i[-1]) {
                *i++ = *iaux2[1]++;
            }
        else {           // caso G
            tramonuevo = true;
        }
    }
    delete[] aux[1];
    delete[] aux[0];
    return tramo;
}

Ejecutar este código en OnlineGDB.